楽しい確率シミュレーション
公開日
2021年7月4日
更新日
2021年7月4日

数学講師の松中です。先日こちらの記事で、ディズニーツムツムで特定のキャラクターが出る確率を実際に課金して確認しました。
しかしその課金の総額はなんと110,000円!ちょっとした好奇心で実験するにしてはお金がかかり過ぎです。
そこで今回はコンピュータを使ったシミュレーションについて紹介したいと思います。シミュレーションとは、コンピュータの中で仮想的に模擬実験を行うことです。コンピュータの中では条件を変えて実験したり、何万回も繰り返して実験したりといったことが容易にできるので、時間やリソースの制限、倫理的な制約などから、簡単に行うことができないような現実世界の実験に対してとても有効です。例えば新型コロナの感染者数の増減の予測や、感染対策の効果測定などにもシミュレーションが用いられています。今回のディズニーツムツムの実験についても、課金せずに何万回もガチャを行うことができるのです。
本記事ではシミュレーションの題材として高校数学の確率の問題を取り上げます。私は普段数学を教えているので、確率の計算をすることは多くあります。授業の中で問題の答えの確率が\(\frac{12}{37}\)と出たときに、果たしてそれは本当だろうかと思うことがあります。何か条件が漏れているとか、重複して数えているとか、そういった計算ミスがないか気になってしまいます。確率は面積や長さのように物理的に存在するものではないため、正しいか正しくないかは直感的にしかわかりません。
そこで活躍するのがシミュレーションです。実際にその問題の設定をプログラムで表現し、実験を100万回繰り返し行います。その結果確率を計算する事象が\(324,121\)回発生したとすると、\(324,121/1,000,000=0.324121\simeq \frac{12}{37}\)となって、確率の答えが合っていそうだと自信が持てるのです。
プログラミング言語としてはPythonを用いますが、基本的にはどの言語でも問題ありません。しかしPythonは便利なライブラリがたくさん揃っていておすすめではあります。
この記事の主な内容
問題1:カードの問題
まずは普通に数学で解いてみます。カードの取り出し方は\({}_{12} \mathrm{C}_3=\frac{12\times 11\times 10}{3\times 2\times 1}=220\)通りです。そのうち最大値が\(8\)になるのは、1枚が\(8\)でそのほかの2枚が\(1\)~\(7\)のうちのいずれかである場合なので、\(1\times {}_7 \mathrm{C}_2=21\)通りです。よって確率は\(\frac{21}{220}\)となり、これは小数で表すと約\(0.095454\)となります。
それでは実際にシミュレーションを行ってみます。3枚カードを取り出すという試行を100万回繰り返し、結果、最大値が\(8\)になる回数の割合が\(\frac{21}{220}\)に近いことを確認しましょう。
プログラムを書くと以下のようになります。
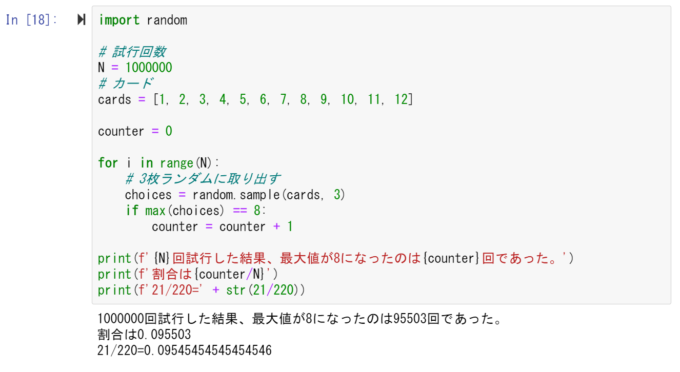
結果、100万回実験して、最大値が\(8\)になったのは\(95,503\)回。その割合はたしかに\(\frac{21}{220}\)に近い値になっています。もちろん完全に一致するわけではないですが、確率が正しそうであると確信が持てる結果です。
プログラムの内容については解説しませんが、現実世界の設定をいかにプログラムに落とし込むか考えるのははなかなか面白いです。興味を持った方は勉強、挑戦してみてください。
100万回カードを引き、最大値が\(8\)かどうか調べて、\(8\)であったらカウントするといった作業を人間がやろうとするととてつもなく時間がかかるでしょうし、ミスも多発するでしょう。実際上記の一連の操作を5秒でできたとしても、100万回繰り返すと、500万秒(≒58日間)かかる作業です。時給1,000円でアルバイトを雇って実験してもらうと単純計算で139万円かかります。
しかし、先のプログラムはほんの数秒で完了しますし、給料を払う必要もありません。シミュレーションの有用さを物語っていないでしょうか。
問題2:赤玉白玉問題(条件付確率)
こちらもまずは数学で解きましょう。これは条件付確率と言われるものです。1回目に赤玉が出ているので、2回目に玉を取り出す直前の袋の中身は、赤玉が\(7\)個、白玉が\(6\)個です。よって1回目に赤玉が出たとき、2回目に白玉が出る確率は\(\frac{6}{13}\)となります。
ではシミュレーションで確認してみましょう。

こちらも小数点以下3桁まで一致していますね。
問題3:不良品の問題(ベイズの定理)
ちょっと複雑ですが、ザ・ベイズの定理と呼んでいいくらい基本に忠実な問題です。まずは数学で答えの確率を求めます。
検査した製品が機械Aで作られたという事象を\(A\)、機械Bで作られたという事象を\(B\)、不良品であるという事象を\(E\)とすると、\(P(A)=\frac{7}{10}\)、\(P(B)=\frac{3}{10}\)、\(P_A(E)=\frac{3}{100}\)、\(P_B(E)=\frac{5}{100}\)となります。
求めたい確率は\(P_E(A)\)ですから、ベイズの定理より、
\[
P_E(A)=\frac{P(A)P_A(E)}{P(A)P_A(E)+P(B)P_B(E)}=\frac{\frac{7}{10}\times\frac{3}{100}}{\frac{7}{10}\times\frac{3}{100}+\frac{3}{10}\times\frac{5}{100}}=\frac{7}{12}
\]
問題設定は先の2題より複雑ですから、求めたい確率が\(\frac{7}{12}\)なることは直感的には明らかではありません。ではこちらも100万回検査を行うというシミュレーションしてみます。

こちらも小数点以下3位まで一致しているので正しそうです。
ツムツムのシミュレーション
では最後にツムツムのシミュレーションをしてみましょう。
プログラムはこんな感じになります。

ガチャ回数(試行回数)の\(N\)を変化させて実際に出てきたツムの割合を見ていきます。まずは\(32\)回ガチャを行います。現実世界ではこれだけで11,000円も必要のようです。結果は前回の記事で書かれてあった通り、1回も引かれないツムもあるようです。割合はご覧の通りバラバラです。
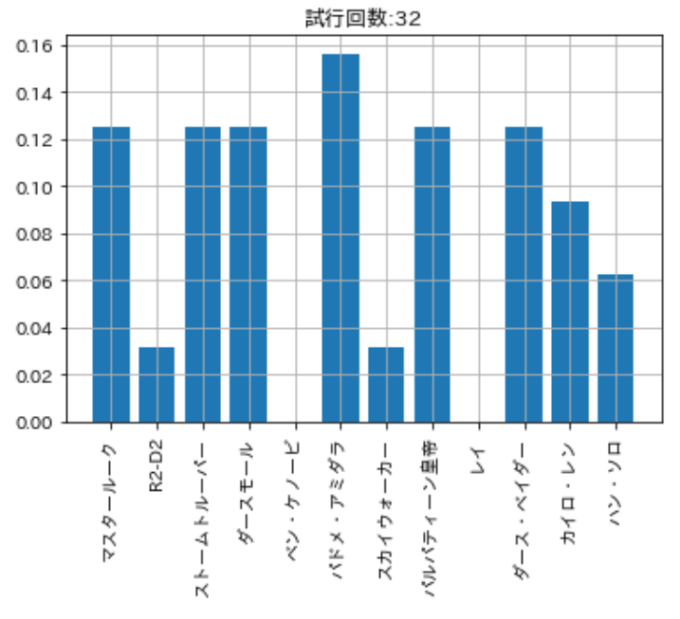
ガチャ回数を\(100\)にしてみました。さすがにどのツムも1回以上は出ています。割合もまだまだバラバラですね。
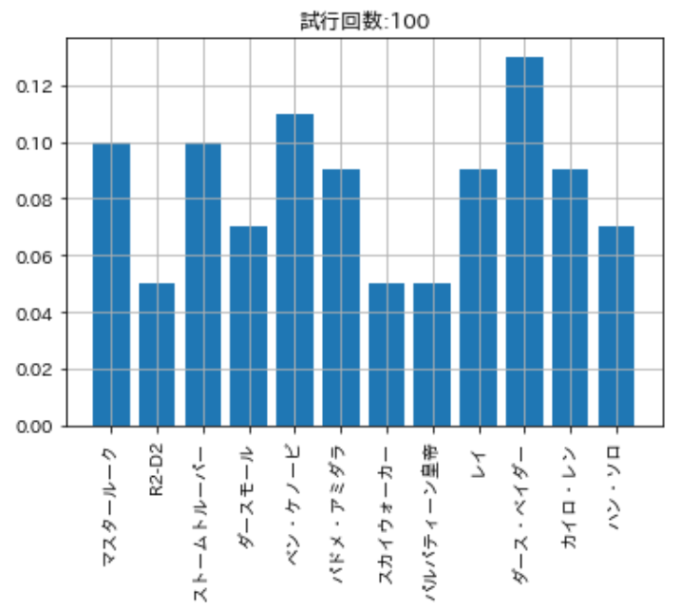
前回の記事で行ったガチャの回数\(320\)です。やはりまだばらついています。
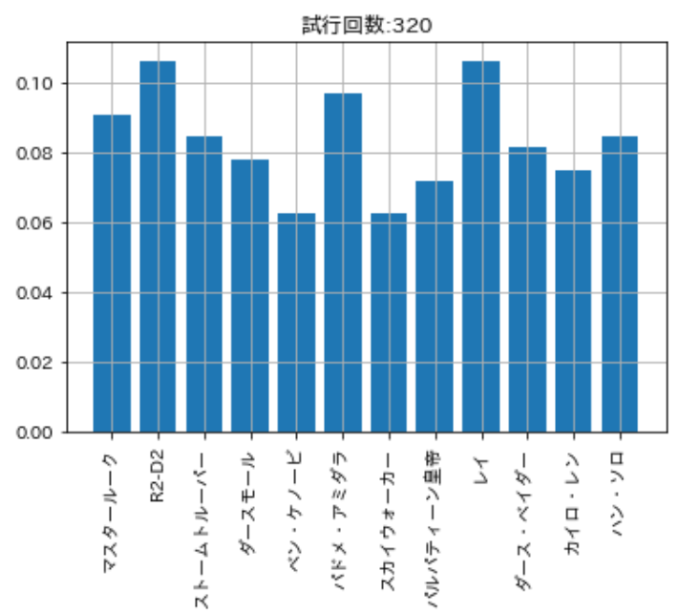
ガチャ回数を\(1,000\)にしてみました。割合のばらつきが小さくなったようです。
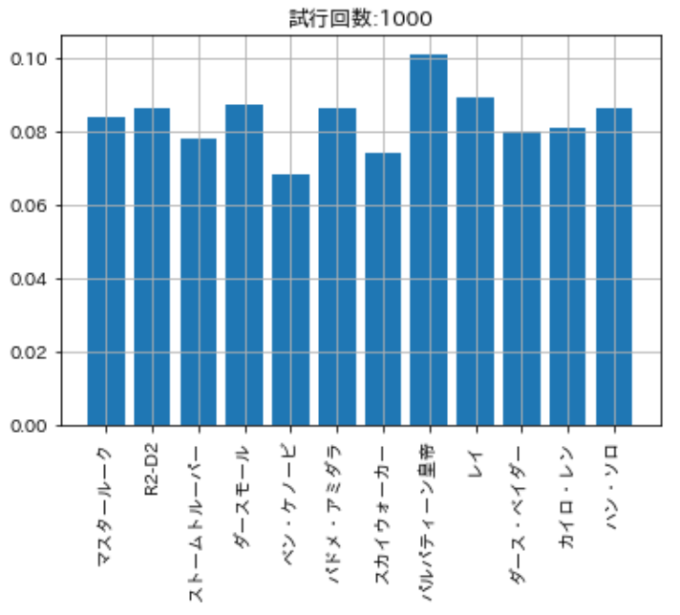
ガチャ回数を\(10,000\)にすると、割合のばらつきがほとんどなくなります。
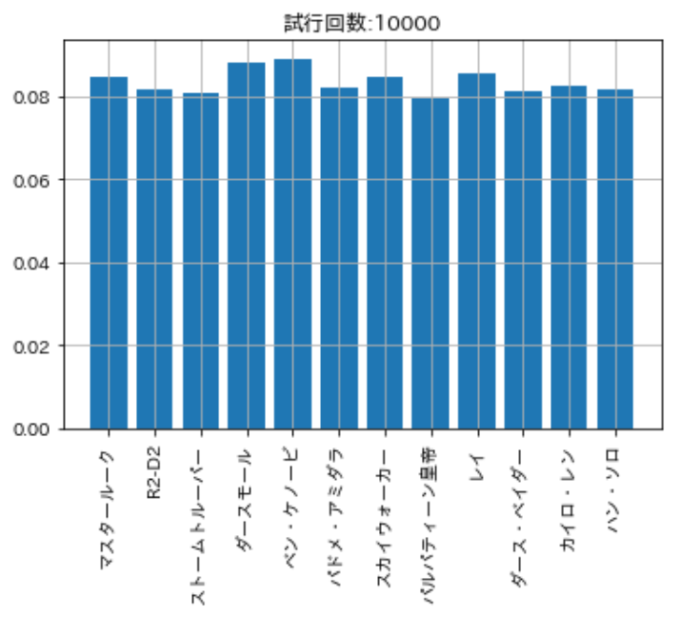
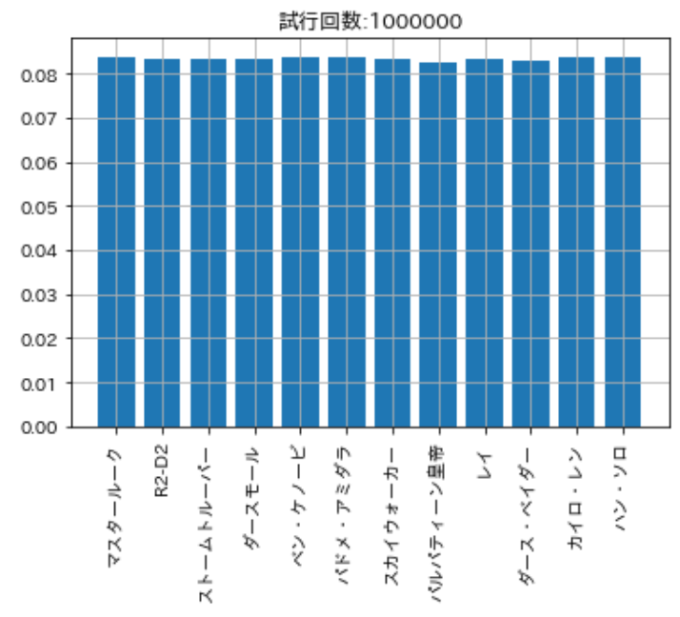
最後にガチャ回数を\(1,000,000\)にしてみました。実際に課金していたら3億4千万円ほどかかりますが、シミュレーションなら無料の上、3秒くらいで結果が出ます。このように割合のばらつきはもうありません。これが大数の法則と呼ばれるものです。
さいごに
今回は確率の結果をシミュレーションで確認する様子や、大数の法則を実感できるシミュレーションを紹介しました。確率のシミュレーションも面白いですが、個人的には物理のシミュレーションもとても面白く感じます。例えば、地球、と太陽を模した点を用意し、万有引力に従って地球、太陽がどのように運動するのかを観察するとなかなか面白いです。地球に初期値として与える速度や位置が変化すると、その軌道が楕円になったり、双曲線になったり、太陽に沈んで行ったりします。
今回のプログラムはどれも短いものでしたが、これはPythonのライブラリのおかげです。またPythonには可視化のライブラリ、アニメーションを作成するライブラリもそろっており、簡単にシミュレーションができます。皆さんも興味があればシミュレーションして遊んでみましょう。
<文/松中>













