やさしく学ぶ統計学~順列の応用と重複順列~
公開日
2023年4月12日
更新日
2023年4月12日

みなさんこんにちは。和からの数学講師の伊藤です。今回は、以前の記事で紹介した順列の考え方の応用と、重複順列と呼ばれる考え方についてのお話です。以前の順列の内容との違いも理解して使いこなせるようになりましょう!
↓以前の順列の記事
この記事の主な内容
1. 対照を区別しない順列
今回は、次のような問題を考えましょう。
➁青色の玉3個と赤色の玉4個を1列に並べる。
➀の問題は前回紹介した順列の問題です。まずはこの2つの問題の違いを解説します。➀の問題については、次のような並び方を全て別の並びとして考えます。
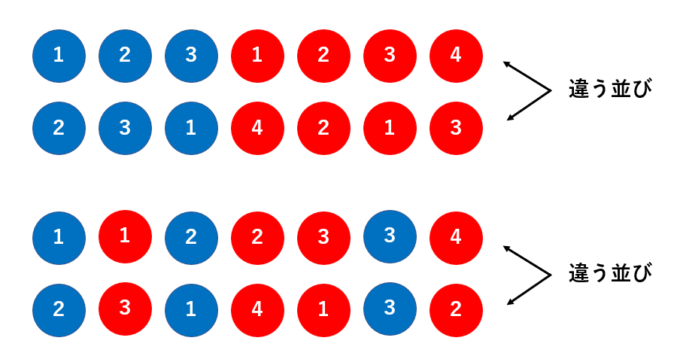
全ての玉が異なるので、これらの玉を並べる並べ方は、\( 7! = 5040 \)通り存在します。一方➁の問題については、上のように番号付けされていません。よって、同じ配色の並べ方は全て同一視して考えます。
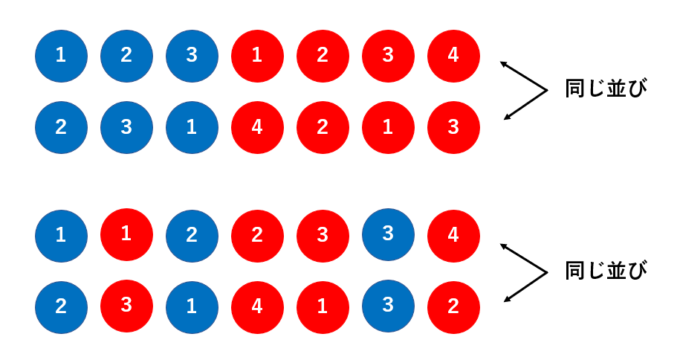
このような対象を区別しない場合の並べ方について、場合の数を計算してみましょう!
2. 対象を区別しない順列の計算方法
まず、玉が以下のように並んでいる状況を考えます。

玉に番号がついている場合、3つの青い玉の並び方が\( 3! \)通り、4つの赤い玉の並び方が\( 4! \)通り存在するため、上のような「青青青赤赤赤赤」という配置の並べ方は\( 3! \times 4! \)通り存在します。
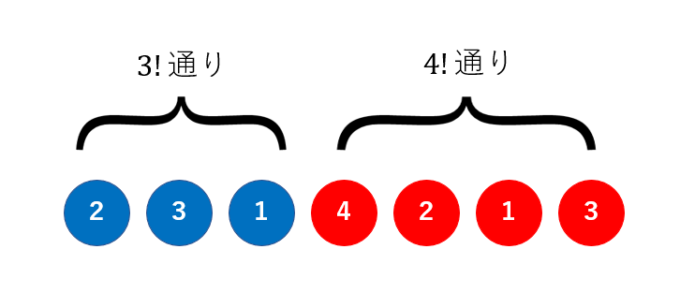
同じように考えると、問題➁で考える並べ方のそれぞれに対して\( 3! \times 4! \)通りの並べ替えが考えられます。逆に考えると、異なる7個の玉を並べる場合の数である\( 7! \)を\( 3! \)と\( 4! \)で割ったのもが、➁の並べ方の数に一致します。
よって、同一の\(m\)個の物と\(k\)個の物を1列に並べる場合の場合の数は、以下のように計算できます。
\begin{align*}
\frac{(m+k)!}{m!k!}
\end{align*}
3. 最短経路の場合の数
次に、対象を区別しない順列の典型的な例をお話します。次のような碁盤の目状の経路がある場合に、地点Aから地点Bに行くまでの最短の経路が何通りあるかという問題です。

今回の場合、「右に進む」という操作を4回と「上に進む」という操作を3回行う場合のすべてが最短経路になっています。先ほどの問題と照らし合わせてみると、「→」と書かれた4個の玉と「↑」と書かれた3個の玉を1列に並べ、その並び順の通りに進む道順が、今回の場合の数に対応します。
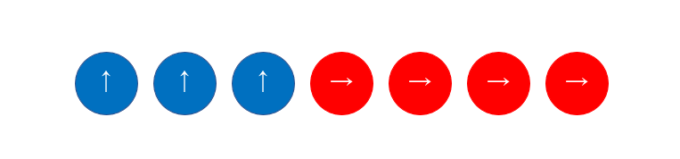
よって今回の道順は、先ほどと同様に\( 7! \div (3!\times4!) =35 \)通り存在すると分かります。順列の考えを取り入れることで、このような問題も見通しが良くなるのです!
4. 重複順列
最後に、重複順列と呼ばれる順列の考え方を紹介します。
重複順列とは、同じものを繰り返し使用することが許されるときの順列のことを言います。今回は例として赤青2種類の玉があり、玉を横一列に5個並べる場合の数を考えます。今回の場合、どの位置にも赤、青両方の玉が入り得るため、たとえば先頭の玉の配置の仕方は2通りあることが分かります。同様に、全ての位置において玉の配置の仕方は2通りです。
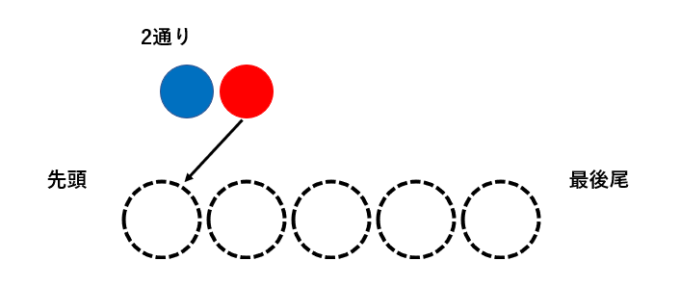
以上から、玉の並べ方の総数は\(2 \times 2 \cdots \times 2 = 2^5\)と計算できます。
同様に、\(n\)種類の要素があり、それぞれの要素を無制限に使用できる状況で\(r\)個の要素を選んで並べる場合の数を求めるときも、\(n^r\)と計算することができます。
今回の記事で紹介してきた考え方を用いると、重複した物の組み合わせを求める「重複組み合わせ」も理解できます。次回はこの重複組み合わせに関しても解説しますので、ぜひそちらもご覧ください!
●和からのセミナー案内
Excelを用いたデータ分析のストーリーや可視化のスキルを学んでいくセミナーのご紹介です。興味を持っていただけた方は、ぜひ覗いてみてください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>













