【パズル的数学】2次関数と図形の問題②～エレガントな別解を味わう～

算数・物理・数学トピック

公開日

2023年4月9日

更新日

2023年4月9日

みなさんこんにちは！和からの数学講師の岡本です。以前、マスログで以下の話題を扱いました。

放物線上の３点をもつ平行四辺形の面積の問題です。今回はその続きということで別の解法をご紹介しようと思います。

この記事の主な内容

１．2次関数と平行四辺形の問題（再掲）

まずは問題を思い出してみましょう。

【問題】2次関数

$y=x^2$ で与えらえる曲線

$C$ と２つの平行な直線

$L_1$ :

$y=ax+b$ ,直線

$L_2$ :

$y=ax+c$ を考えます。ただし、

$a, b, c$ は正の実数であり、

$b>c$ とします。このとき

$C$ と

$L_1$ の２つの交点をA,B、

$L_2$ との交点をC,Dとします。また、ADとB’Cが平行になるように線分AB上に点B’を考えます。このとき、平行四辺形AB’CDの面積を

$a, b, c$ を用いて表して下さい。

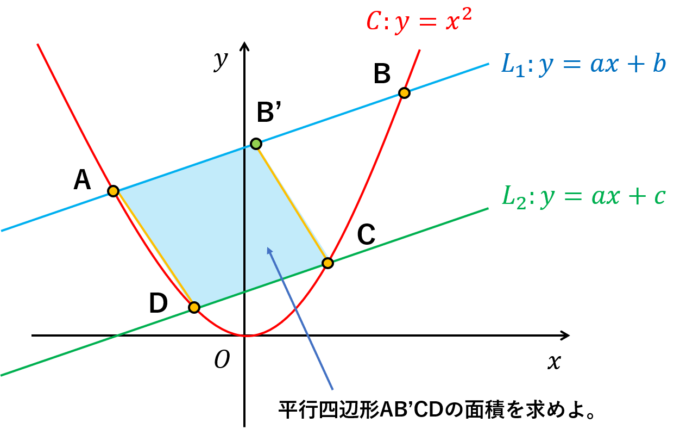
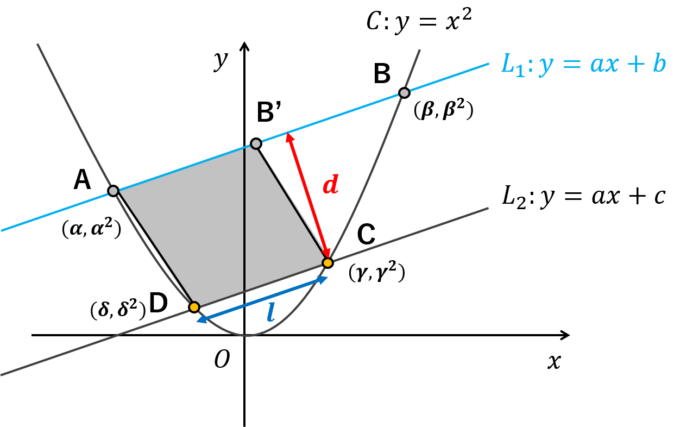
「平行四辺形の面積＝底辺×高さ」という公式に注目し、前回は下図のように底辺 $L$ と高さ $d$ を力技で求め、面積を計算しました。今回はもう少し「エレガント」な解法をご紹介します。

２．線形代数の力をお借りする

$\overrightarrow{\mathrm{DA}}$ と $\overrightarrow{\mathrm{DC}}$ が成分で表すことができれば、この２つのベクトルで張られる平行四辺形の面積は「行列式」を使って1発で計算することができます。今回、点A、点D、点Cの座標は二次関数と直線の交点であり、それぞれA $(\alpha, \alpha^2$ ),D $(\delta, \delta^2)$ ,C $(\gamma,\gamma^2)$ と表すことにします。すると

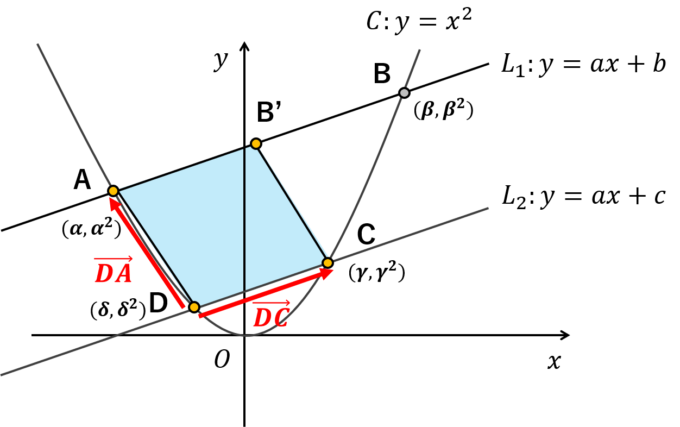
$\begin{align*} \overrightarrow{\mathrm{DA}}=\begin{pmatrix}\alpha-\delta \\ \alpha^2-\delta^2 \end{pmatrix}, \overrightarrow{\mathrm{DC}}=\begin{pmatrix}\gamma-\delta \\ \gamma^2-\delta^2 \end{pmatrix}, \end{align*}$

であり、２つのベクトルで張られる平行四辺形の面積 $S$ は２つの縦ベクトルを横に並べることで得られる２×２の正方行列の行列式の絶対値で計算できます。

$\begin{align*} S&=\left|\det \begin{pmatrix} \alpha-\delta & \gamma-\delta \\ \alpha^2-\delta^2 & \gamma^2-\delta^2 \end{pmatrix}\right|\\ &=|(\alpha-\delta)(\gamma^2-\delta^2)-(\gamma-\delta)(\alpha^2-\delta^2)|\\ &=|(\gamma-\delta)\{(\alpha-\delta)(\gamma+\delta)-(\alpha^2-\delta^2)\}| \end{align*}$

ここで、 $\delta, \gamma$ は2次方程式 $x^2-ax-c=0$ の解なので、 $\gamma+\delta=a$ であり、2次方程式の解の公式から

$\begin{align*} \gamma-\delta=\frac{a+\sqrt{a^2+4c}}{2}-\frac{a-\sqrt{a^2+4c}}{2}=\sqrt{a^2+4c} \end{align*}$

であることがわかります。また、 $\alpha^2=a\alpha+b$ , $\delta^2=a\delta+c$ と表すことができるので

$\begin{align*} S=|(\gamma-\delta)\{a(\alpha-\delta)-a(\alpha-\delta)-(b-c)\}=|(\gamma-\delta)(-b+c)|=(b-c)\sqrt{a^2+4c} \end{align*}$

となり、面積を求めることができました（前回の記事と同じ式が得られました）。

３．図形の性質をうまく利用する方法

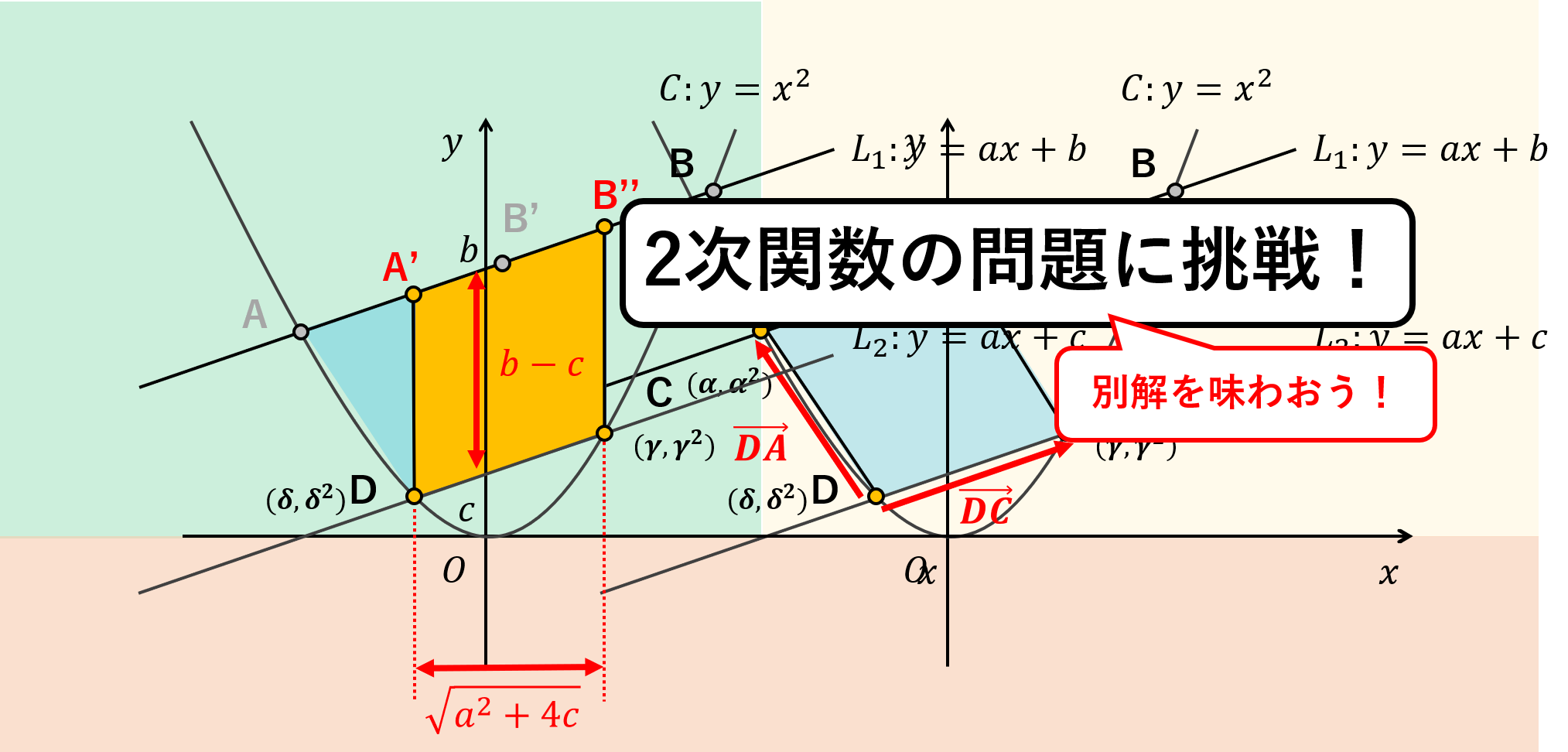
もう一つ解法をご紹介します。これは最も素朴で、最も簡単な方法です。まず、点Aと点B’をAB’の長さを変えずにA’Dが $y$ 軸と平行になるように直線 $L_1$ 上で移動させます。

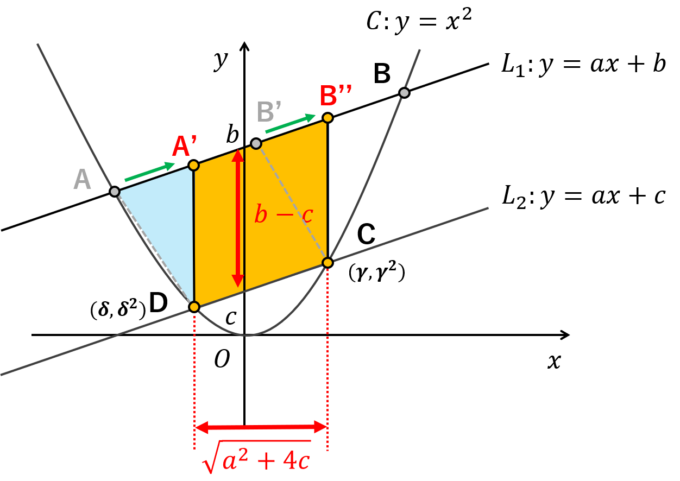
こうしてできる平行四辺形A’B”CDはもとの平行四辺形と同じ面積 $S$ になります。A’Dの長さは $L_1$ と $L_2$ の切片の幅と同じ $b-c$ となります。また、底辺をA’Dと考えると高さは幅 $\gamma-\delta=\sqrt{a^2+4c}$ であるので、求める面積 $S$ は

$\begin{align*} S=(b-c)\sqrt{a^2+4c} \end{align*}$

であることがわかりました。こうした、面積を同じにしたまま図形を変形させることを「等積変形」と呼びます。