↓↓↓動画で見たい方はこちら↓↓↓

みなさんこんにちは。和からの数学講師の伊藤です。今回は、統計学や機械学習の手法の中でも、データの情報の縮約に使われることが多い主成分分析と呼ばれる手法について見ていきたいと思います。ビッグデータという言葉がいたるところで見られるようになっている現代では、役に立つ場面も多いかもしれません！

１．主成分分析とは？

データを収集する際には、一度に複数の項目を調査することが多いです。たとえば学校の体力テストでは、50メートル走やボール投げなど、10個程度の項目を検査しています。こういった観測項目の数を、統計学の世界ではデータの次元と呼びます。

主成分分析というのは、複数の項目を計測したデータがあるときに、それをごく少数の項目に置き換えることで、データを解釈しやすくする手法のことです。データを眺める視点をある特定の方向に絞ることで、全体の傾向を要約できるというメリットがあります。

「次元」という数学の言葉を使って説明すると、次元の高い空間に散らばっているデータを、2次元や3次元といった低い次元に射影(縮約)することで、データを解釈しやすくしたり、視覚化できるようにするといった手法です。このことから、主成分分析は次元の縮約、次元の削減として使われます。

以下、この話を視覚的に見ていきましょう。

２．主成分分析を図で考えてみる

今回は例として、3次元のデータを1次元に縮約するといった方法を見ていきます。つまり3つの観測項目があったデータの情報を、1本の数直線上に集約して見てみようということになります。今回は次のようなデータを作ってみました。とある駄菓子屋さんでの、1か月間のそれぞれの属性の商品の売り上げデータです。

このデータを3次元空間に可視化してみると、次のような散布図が描けます。

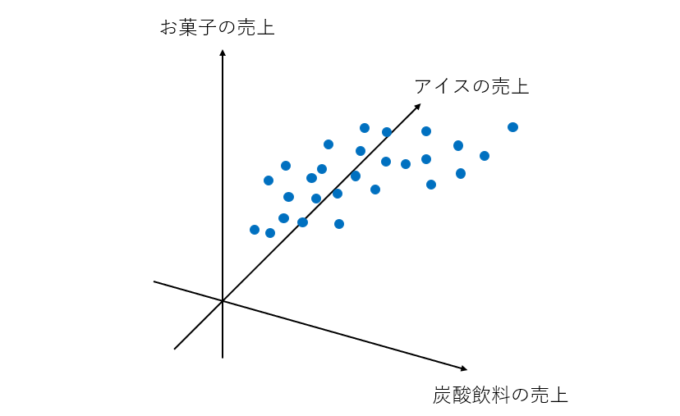
主成分分析で行っていくのは、このデータの特徴を最もよく表している方向を一つ定めて、その方向へのデータの散らばり具合を分析するというものです。先ほどの図を見てみると、このデータは、「炭酸飲料の売上」という項目と「アイスの売上」という項目のちょうど間の部分にデータが広く分布しています。つまりここが、データの特徴が最もよく現れている部分ということです。

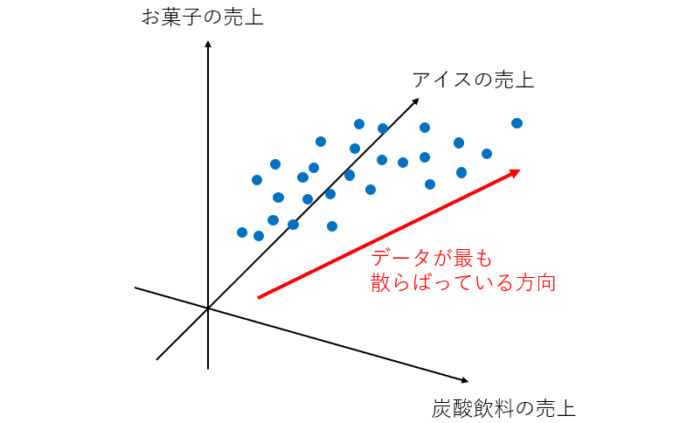
ということで、この方向に数直線を引いてみて、その数直線上にデータを縮約していきます。数学的な説明は後の章に譲って、今回はイメージで見てみましょう。数直線上に、次のようにデータが縮約されます。

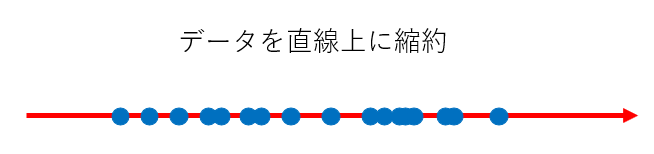
3次元の空間の中でばらついていたデータが、一つの数直線に乗ったことでとても見やすくなりました。これが主成分分析のイメージになります。4次元より大きい世界は我々の目で見ることはできないのですが、主成分分析で次元を縮約することで、目で見えるようにデータを要約することもできるのです！

1つ注意したいのが、もともとのデータを無理やり要約しているので、一部の情報を捨ててしまっているというデメリットもあります。主成分分析はうまく使わないと、せっかくたくさんの項目を観測しているのにそれらの情報が無駄になってしまいます。

３．数学的な説明

では先ほど視覚的に見ていった主成分分析の方法を、もう少し正確な数学の言葉で見ていきましょう。

データを一つの方向から見るということは、その方向に引いた軸上にデータを正射影するということになります。そして、データが最も散らばっている方向というのは、分散が最も大きくなる方向という意味になります。つまり主成分分析とは、正射影したデータの分散が最大になる軸を決定するという考え方になります。

こういった考え方に従って、データの分散が最大になる方向を実際に計算してみると、データの標本共分散行列の第一固有ベクトルを求れば良いということになります。また、データを1次元ではなく2次元に縮約したいと思ったら、今度は第二固有ベクトルを求めて、第一固有値と第二固有値がなす平面にデータを正射影していけばよいということになるのです。このようにして、必要な数の軸（つまり次元）を用意して、その世界にもとのデータを正射影するというのが、主成分分析の計算になります。

ここで疑問になるのは、いったいいくつの主成分を用いればよいのかといった点です。この疑問には、寄与率という概念を使って答えることができます。k個の主成分を使ってデータを縮約するときの寄与率とは、標本共分散行列の固有値の総和と、k番目までの固有値の総和の比になります。つまりk番目までの固有値が全体に占める割合が大きければ多きいほど、データの特徴を説明できているということになるのです。分析をする際には、たとえば「寄与率が80%を超えるまで主成分を求める」という方法で、いくつの主成分を採用するかを決めたりします。

４．まとめ

いかがでしたでしょうか。複雑化してきた現代のデータに対してピッタリな、主成分分析という手法の紹介でした。

さて、以前のマスログでは、現代のデータの中でもとくに次元(観測項目の数)が多い、高次元データと呼ばれるデータをご紹介してきました。高次元データに対して、次元を削減する主成分分析は相性◎なのでは…と思いきや、実は高次元データに主成分分析を適用する際には、思いもよらない問題が発生するのです。ということで次回、その問題点と解決の糸口についてのお話も記事にしていきます。お楽しみに！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/伊藤智也>

駄菓子詰め合わせお楽しみ50種55点セット＋おまけおもちゃ付き