↓↓↓動画で見たい方はこちら↓↓↓

空間図形（立体）とは

今回は「球」について考えていきますが、まずは立体の復習をしましょう。空間図形（立体）とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。
立体にはどのようなものがあったのかをまとめた記事があるので、立体について少し心配な方は以前の記事をぜひご覧ください。
（参考：空間図形（立体）の総復習（球編）【算数からやさしく解説】）

球の体積

球の体積を厳密に求めるためには、基本的に積分という概念が必要になってしまいます。
なので、一旦は球の体積の公式を覚えてしまうのが良いと思います。球の体積を求める式は以下のようなものです。
（球の体積）\(=\frac{4}{3}×\pi×（半径）^3\)
球にはどこを平面で切り取っても断面が円になるような性質があるように、円と非常に関係が深いので球の体積の式には\(\pi\)が入っています。

球の表面積

次に球の表面積の式についてもみていきたいと思います。
表面積の式は体積の式と似ているので、ここで一緒に扱ってしまいたいと思います。表面積の式は以下のようになります。
（球の表面積）\(=4×\pi×\) （球の半径）\(^2\)
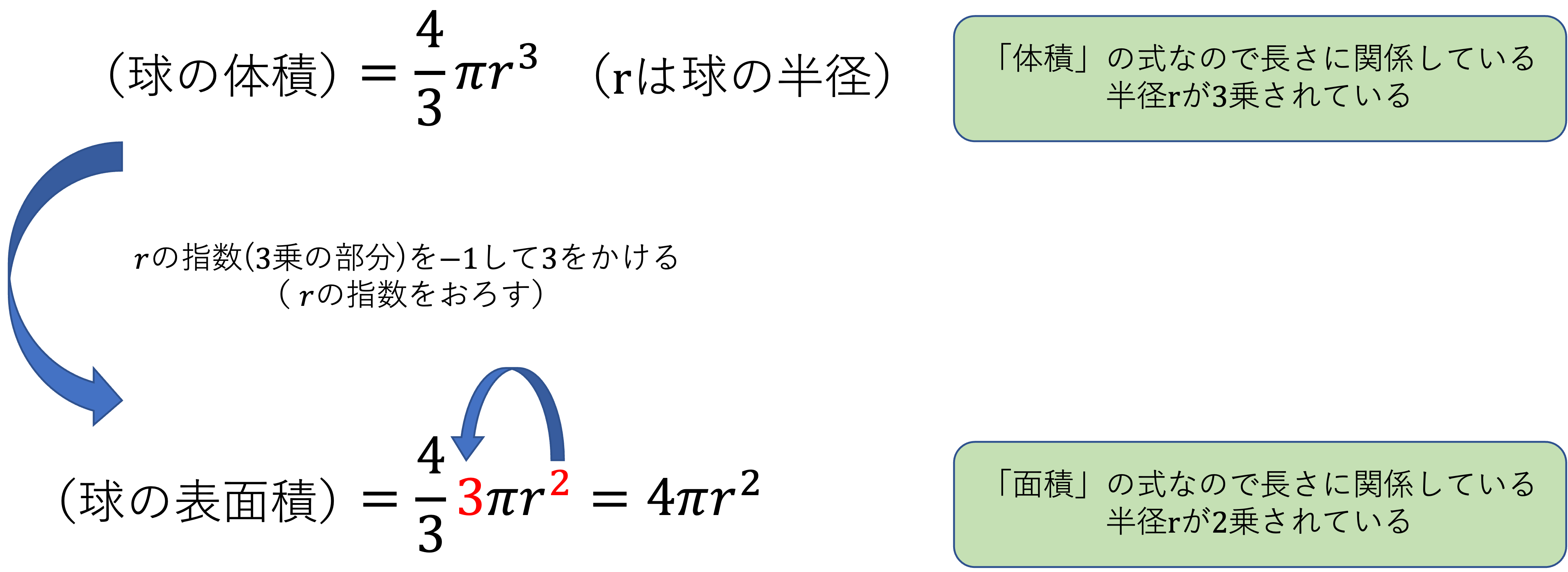
表面積の式は下図のような操作を考えれば体積の式から表面積の式を導く事ができます。これは微分と呼ばれる操作なのですが、直接式に関係するものではないので覚え方の１つとして参考程度に見てみてください。

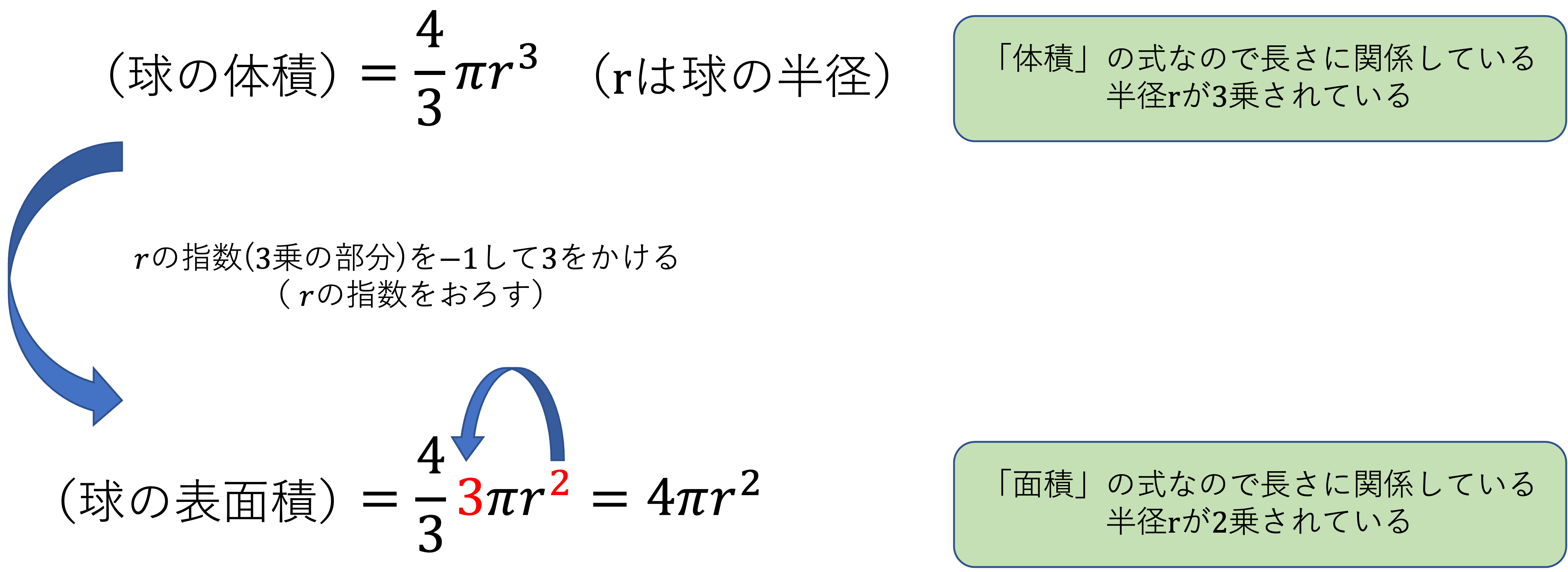
また、「空間図形（立体）の体積（直方体・立方体編）」の最後で紹介したように、体積を求める式では長さに関する値である半径が\(3\)つ、表「面積」には半径が\(2\)つ分含まれています。

球の体積の活用

先ほど説明したように、球の体積や表面積を求める式を導くためには積分という概念を使う必要があります。
また、円柱と円錐の体積を求める式がわかっていれば、カヴァリエリの原理というものを使えば直感的に式を導く事ができます。気になった方は是非調べてみてください。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/尾崎>