動画で見たい方はこちら↓↓↓

空間図形（立体）とは

空間図形（立体）とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。前回は説明をしました。今回は生活の中でもよく目にする球について解説していきたいと思います。
前回の記事はこちらになりますのでぜひご覧ください。
（参考：空間図形（立体）の総復習（四角柱、四角錐・円柱、円錐編）【算数からやさしく解説】）

円について

球とは3次元での円のようなものです。なので、球についての解説をする前に円について考えてみましょう。
円とは中心からの距離が等しい「平面上の」点の集まりのことです。
円はコンパスで考えるとわかりやいです。コンパスの針が刺さっている場所が円の中心になっており、ハリとの距離を一定に保ちながら鉛筆の方を回すと円ができます。
このとき、針と鉛筆の長さは固定されているので、円のどの点も中心との距離が一定になっています。

球について

円の考え方をそのまま使って球について考えてみると、
球とは中心からの距離が等しい「空間上の」点の集まりのこと
となります。
球の形はサッカーや野球のボールなんかを想像してもらえればわかると思いますが下図のようになります。

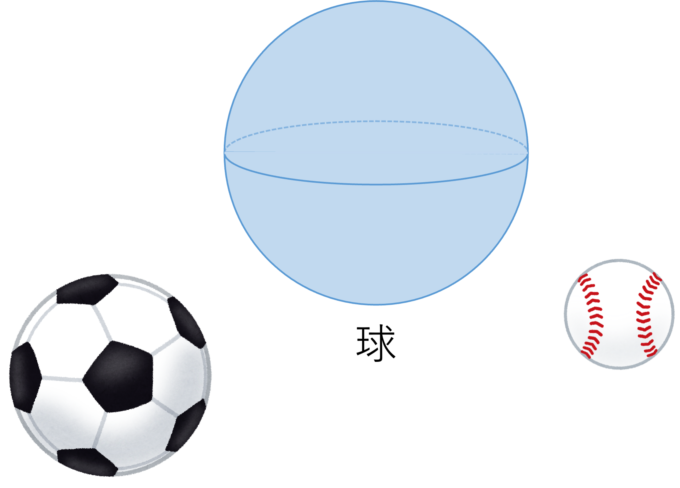
円の時と同様に球のどの点も中心からの距離は等しくなっています。
球は今までの立体と違い平面になっているところがなく、体積や表面積の求め方も他の立体とは異なっています。
また球には、どの角度から見ても円になったり、どんな場所で切っても断面が円になったりする性質があります。

球の活用

球の説明をする際に「距離」が出てきましたが、私たちが数学などで距離という言葉を使うときは基本的に点と点をつなぐ線分を使って表されます。ですが、実は“距離”の決め方はいくつもあり、それぞれの距離の決め方によって別の“円”や“球”の形が決まります。
例えば、マンハッタン距離と呼ばれる、\(x\)軸、\(y\)軸にいくつ進んだかを使って距離を表すものもあり、その場合の“円”は正方形になることが知られています。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

空間図形（立体）の総復習（四角柱、四角錐・円柱、円錐編）【算数からやさしく解説】

<文/尾崎>