空間図形(立体)の総復習(四角柱、四角錐・円柱、円錐編)【算数からやさしく解説】
公開日
2022年6月17日
更新日
2025年9月18日
動画で見たい方はこちら↓↓↓
この記事の主な内容
空間図形(立体)とは
空間図形(立体)とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。前回は柱や錐のイメージや実際にどのような立体があるかを三角柱、三角錐を例に挙げて説明をしました。今回は四角形や円を使った「柱」や「錐」の形をもつ空間図形について考えていきたいと思います。
前回の記事はこちらになりますのでぜひご覧ください。
(参考:空間図形(立体)のまとめ2(三角柱・三角錐)【算数からやさしく解説】)
四角柱・四角錐について
四角柱、四角錐の考え方はそれぞれ三角柱、三角錐と同じで、立体の形は下図のようになります。
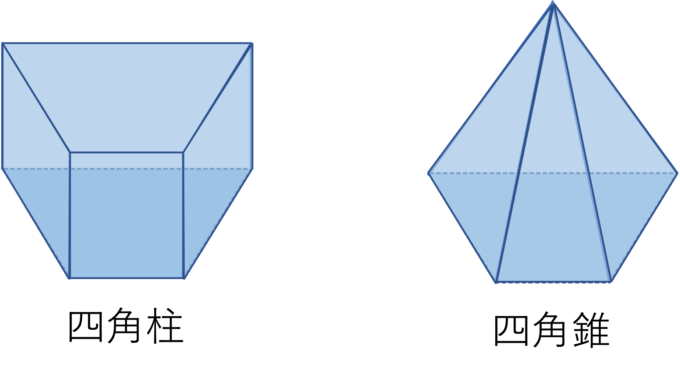
図からもわかるように、四角柱には8個の頂点と12個の辺、そして6個の面があります。同じように四角錐も考えてみると形は下図のようになり、頂点、辺、面はそれぞれ5個、8個、5個になります。
四角柱と直方体は非常に混同しやすいですが、直方体は四角柱の底面が長方形であるような特別なときに使います。逆に言えば、四角柱は直方体の底面がどんな四角形でもいいようなものです。
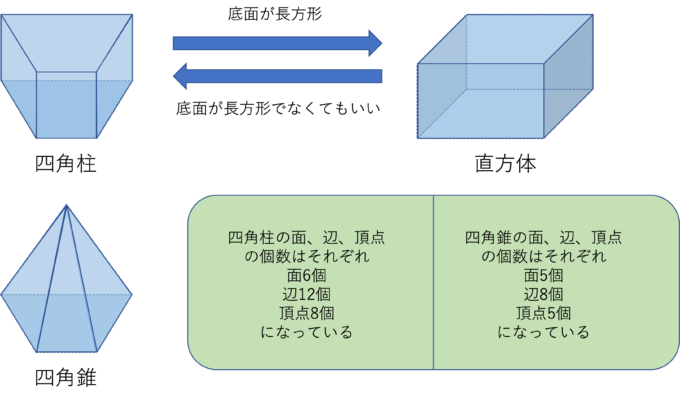
もちろん底面として五角形、六角形、…というように考えていくことはできますが、よく使われるのは三角形、四角形なので今回は割愛させていただきます。
円柱・円錐について
ここまでは、前回と同じように多角形を底面とする「柱」や「錐」を考えてきましたが、次は円を底面とするものについて考えていきます。
とはいっても、基本的にはこれまでの「柱」と「錐」の考え方を使えばどのような形になるかは想像ができると思います。
実際には、円柱と円錐の形は下図のようになります。
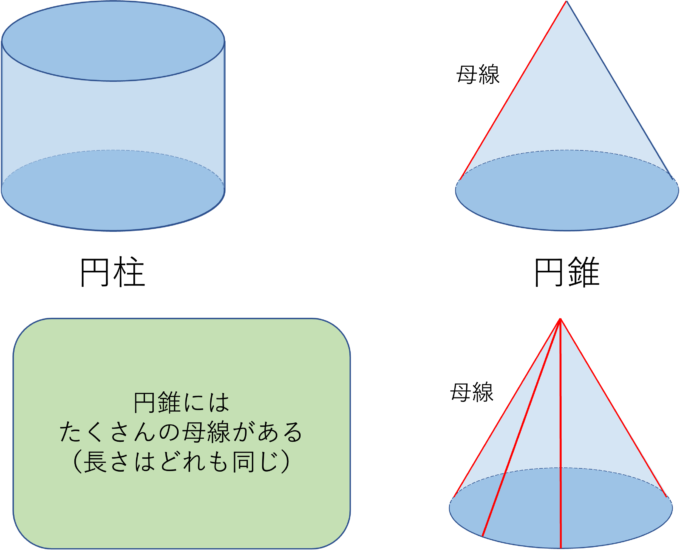
ここで主に円錐に対してのみ使う単語として「母線」というものがあります。これは図のように円錐の頂点から底面の円周までの距離になるような線のことです。
四角錐(柱)・円錐(柱)のまとめ
今回までで様々な「柱」と「錐」の例を見てきました。それぞれ底面が三角形や四角形、円のどれなのか、「柱」なのか「錐」なのかで名前が決まっていました。
実際にこれらの立体が問題として出るときには、体積や表面積(立体の表面の面積)、辺の長さなどを求めさせられることが多いです。
また、問題を解くときには正確な図は非常に便利なので、問題文に図などがついていないことがあっても自分で正確な図が書けるようにできると間違いなどが減るので是非意識してみてください。
次回は、空間図形の紹介の最後として球について解説していきたいと思います。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/尾崎>















