アルキメデスの功績から学ぼう-円周率編-
公開日
2022年7月13日
更新日
2022年7月13日
動画で見たい方はこちら↓↓↓
みなさんこんにちは。和からの数学講師の伊藤です。今回は円周率というテーマでお話をしていこうと思います。先日、数学史上の有名人物であるアルキメデスについての記事を書きましたが、記事を書いている途中で円周率の話題をまとめていたところ、もっとしっかり語りたいと思ってしまったので今回記事にしてみました。明日人に話したくなってしまうような円周率のお話を、ぜひ楽しんでいただければと思います!
この記事の主な内容
1.円周率って何だっけ?
3.141592…でおなじみの円周率は小数点以下無限に続きます。こういった話は有名ですが、円周率って何?と聞かれたら、皆さん答えられますか?これって意外と答えられないものかもしれません。円周率というのは、円の直径に対する円周の長さの比と定められています。どんな円でも直径の長さと円周の長さの比は一定になっていて、この比が3.141592…だったということです。
2.円周率は無限に続く
先ほどもお話しましたが、円周率は小数点以下無限に続きます。私の特技はその円周率を小数点以下100桁まで暗唱することなのですが、これを習得しようと思ったのは中学1年生の時(当時は数学には全く興味がありませんでした)です。当時の数学の先生が、第一回の授業で数学の魅力を簡単にお話してくださったのですが、その話題のひとつが円周率の話題でした。それを聞いて面白い!と思ったので、教科書の後ろの方に載っていた円周率の表を少しずつ覚えていったというのがきっかけです。
さて、中学1年生だった私は円周率を覚え始めたのですが、ある日、こんなことを思いついてしまいました。
「円周率を計算できる数式があれば、覚えなくてもよくないか?」
つまり、たとえば円周率を○○/○○という形の分数で表すことができれば、分子の数字を分母の数字で割り続けることで、いつまでも暗算で円周率を唱え続けられるな、と考えたわけです。とはいえ、この野望は後々になって、「無理数」という言葉を習ったときに消えてしまいました。円周率は分数で表現することができないのです。つまり、割り切れないどころか循環することもなく無限に続いていくということです。
3.円周率の近似を考えてみる
さて、円周率は無限に続くので、暗記や暗算で唱え続けようということはできません。しかし古代から、数学者たちはこの円周率の値を正確にとらえようと奮闘してきました。この近似というテーマに関連して、東京大学の入試問題でも「円周率が3.05より大きいことを示せ」と出題されたこともあります。今回は円周率を近似するという問題を、この入試問題をもとに考えてみましょう。
円周率というのは、直径と円周の長さの比でした。つまり先ほどの東京大学の問題は、「直径1の円の円周の長さが3.05より大きいことを示せ。」と言い換えることができます。この問題を解くためには、次のような発想がカギになってきます。
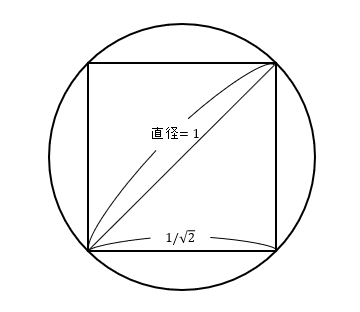
直径1の円と、その中にすっぽり収まる図形を用意する。この図形の周の長さが3.05よりも大きければ、それを覆う円の円周も当然3.05より大きいはず。
前回のアルキメデスの記事でも同じような発想を紹介しましたが、これはどういうことかというと、まず円にすっぽり収まる正方形を考えます。円の直径が1ということから、この正方形の対角線の長さは1となります。すると正方形の1辺の長さが\(1/\sqrt{2}\)ということがわかるので、正方形の周の長さは、\(4 \times (1/\sqrt{2})=2\sqrt{2}\)(\(=2.8\)ぐらい)と求められました。この段階で、円周率は2.8よりは大きいということが分かるのです。
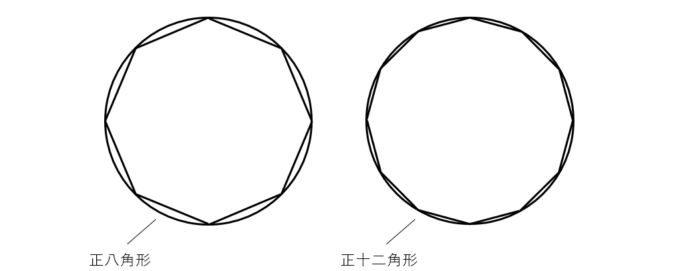
今回はわずかに3.05に及ばなかったので、もう少し大きい図形を考えていくことになります。結局この問題では、正十二角形の周の長さを求める必要がありました。この流れが、古代から円周率を近似するために使われてきた方法になるのですが、アルキメデスが当時行ったとされる近似は、正96角形を使ったものだったそうです。これにより、円周率が3.1408<π<3.1429程度に近似できることを示しています。円周率は3.141592…なので、確かにこのアルキメデスの近似は当たっていたということになります。
4.円周率の現在
ここまで円周率を近似するための古典的な方法を紹介してきましたが、では現在、円周率は何桁くらい計算されているのかというと、数十兆桁はあると言われています。もう途方もない桁数なのですが、いったいそんなにたくさんの桁数をどうやって計算しているのでしょうか。実は現在使われている方法は、古代から伝わる先ほどの方法とは異なっています。コンピュータを使って、無限級数を計算するという形をとっていることが多いのです。これは、たとえば次のような式です。
\[
\begin{align*}
\pi=\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{2k-1}=4 \left( 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots \right)
\end{align*}
\]
\[
\begin{align*}
\frac{1}{\pi}=\frac{2\sqrt{2}}{9801}\sum_{k=0}^{\infty}\frac{(4n)!(1103+26390n)}{(n!)^{4}396^{4n}}
\end{align*}
\]
難しそうな記号が入っていますが、例えば最初の式であれば、分母が奇数になっている分数を無限に足し引きしていった結果、\(\pi\)を含む式が得られたということです。これも結局は無限回の計算が必要になるのでコンピュータで厳密な計算はできませんが、現在のスーパーコンピュータではこういった式を永遠と計算していって、数十兆桁の円周率を求めるための膨大な計算をこなしているということです。現在開発されている量子コンピュータを使えば、この円周率の記録ももっともっと伸ばすことができるかもしれませんね。
5.まとめ
いかがでしたでしょうか。円周率という小学校からおなじみのテーマでしたが、大学入試にまで出題される奥深い内容でした。円周率の近似というテーマには今後も注目していきたいですね。次回はアルキメデスの記事に関連してもう一つ、浮力の記事を書こうと考えています。それでは、また次回のマスログでお会いしましょう!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>














