空間図形(立体)の体積の求め方(直方体・立方体)【算数からやさしく解説】
公開日
2022年6月27日
更新日
2025年9月18日
動画で見たい方はこちら↓↓↓
この記事の主な内容
空間図形(立体)とは
空間図形(立体)とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。
立体にはどのようなものがあったのかをまとめた記事があるので、立体について少し心配な方は以前の記事をぜひご覧ください。
(参考:空間図形(立体)の総復習(直方体・立方体編)【算数からやさしく解説】)
直方体の体積の考え方
体積について考える時に、以前に紹介した面積の考え方と同じように、縦・横・高さが\(1\)であるような立方体をどれだけ入れる事ができるかで考えてもいいのですが、せっかく面積について知っているのでこれを利用して考えてみましょう。
ここでは、体積とは
平面の図形をどれだけ「高さ」の方向に積み重ねたか
で考えましょう。
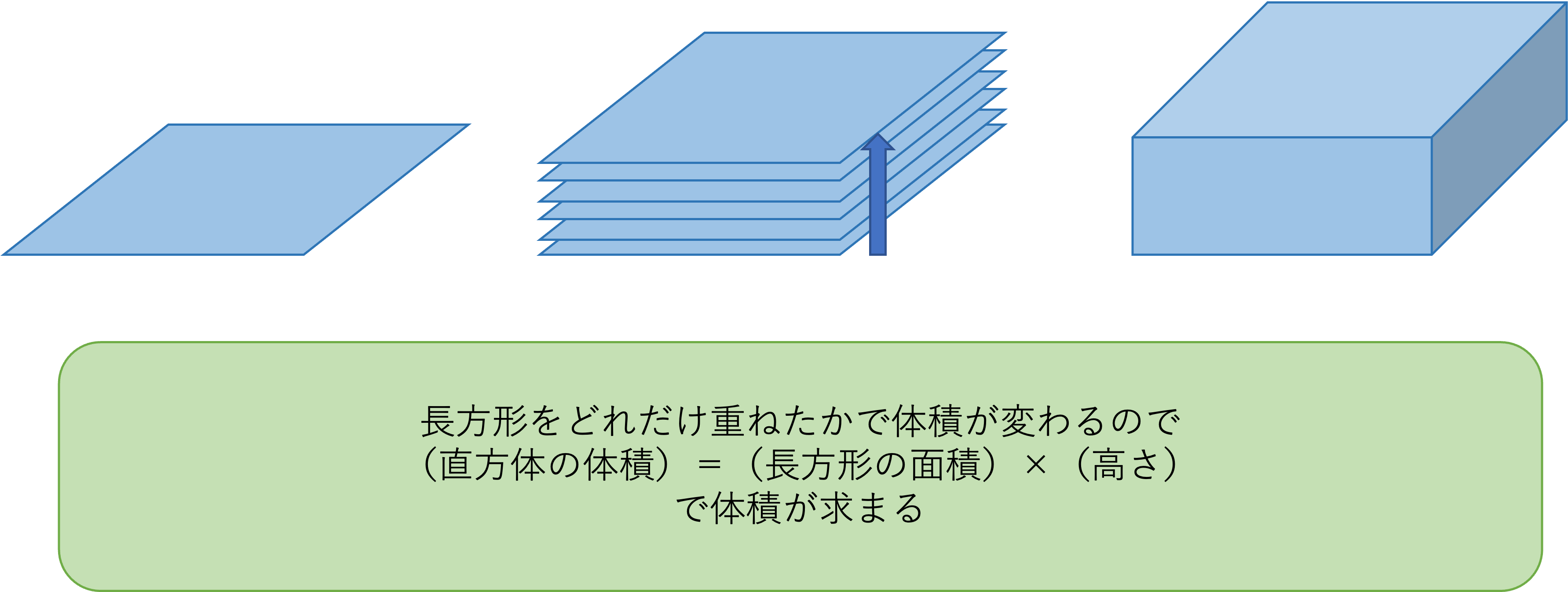
それでは、下図のような直方体の体積について考えてみましょう。
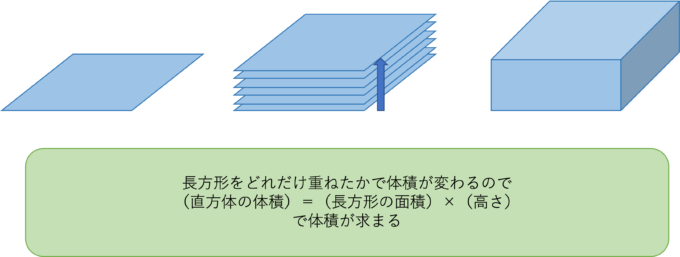
「空間図形(立体)の総復習(直方体・立方体)」でも解説したように、直方体は長方形を「高さ」の方向に重ねたものと考えられました。
この時に、どのぐらいの面積の長方形をどれだけ高く重ねたかでこの直方体の体積がわかります。つまり、
(直方体の体積)=(長方形の面積)×(高さ)
になります。
長方形の面積は(縦)×(横)で求められたので、最終的には
(直方体の体積)=(縦)×(横)×(高さ)
で求められるとわかります。
つまり、直方体は3つの辺の長さが分かれば、それらを掛け合わせたものが体積になるとわかります。
直方体の体積計算の例
先ほど、直方体の体積を求める式の紹介をしたので、実際にどうのように使って行くのかを見てみましょう。
例えば、それぞれの辺が\(2,3,5\)である直方体の体積を計算してみると、先ほどの公式からそれぞれの辺の長さを掛け合わせることで、直方体の体積は\(2×3×5=30\)とわかります。
また、立方体は全ての辺の長さが等しい直方体なので、同じ考え方で
(立方体の体積)\(=\)(辺の長さ)\(^3\)
となります。
例えば、立方体の面積は全ての辺が\(2\)であるような立方体の体積は\(2×2×2=2^3=8\)となる事がわかります。
直方体・立方体の体積の活用
立体の体積を求める時には長さに関する数値に注目すると計算ミスが減ったり、公式の間違いに気づく事ができる時があります。
例えば、今回の立方体の体積に関しては
(立方体の体積)=(辺の長さ)\(^3\)
となっていました。このように体積を求める式には基本的に長さに関する数が(縦、横、高さのように)3つ出てきます。
この考え方は、平面図形の面積を求めるときなどにも同じような考え方が使えて、面積を求める式には基本的に長さに関する数が(縦と横のように)2つ出てきます。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/尾崎>















