↓↓↓動画で見たい方はこちら↓↓↓

空間図形（立体）とは

空間図形（立体）とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。これから複数回にわたって小学校や中学校で扱うような立体について解説していきたいと思います。

直方体について

はじめに解説する立体は直方体です。
直方体とは、長方形（正方形を含む）で囲まれた立体のことです。
長方形や正方形については以下の記事をご覧ください。（参考：四角形の分類【算数からやさしく解説】）
実際に図として書いてみると下図のようになります。
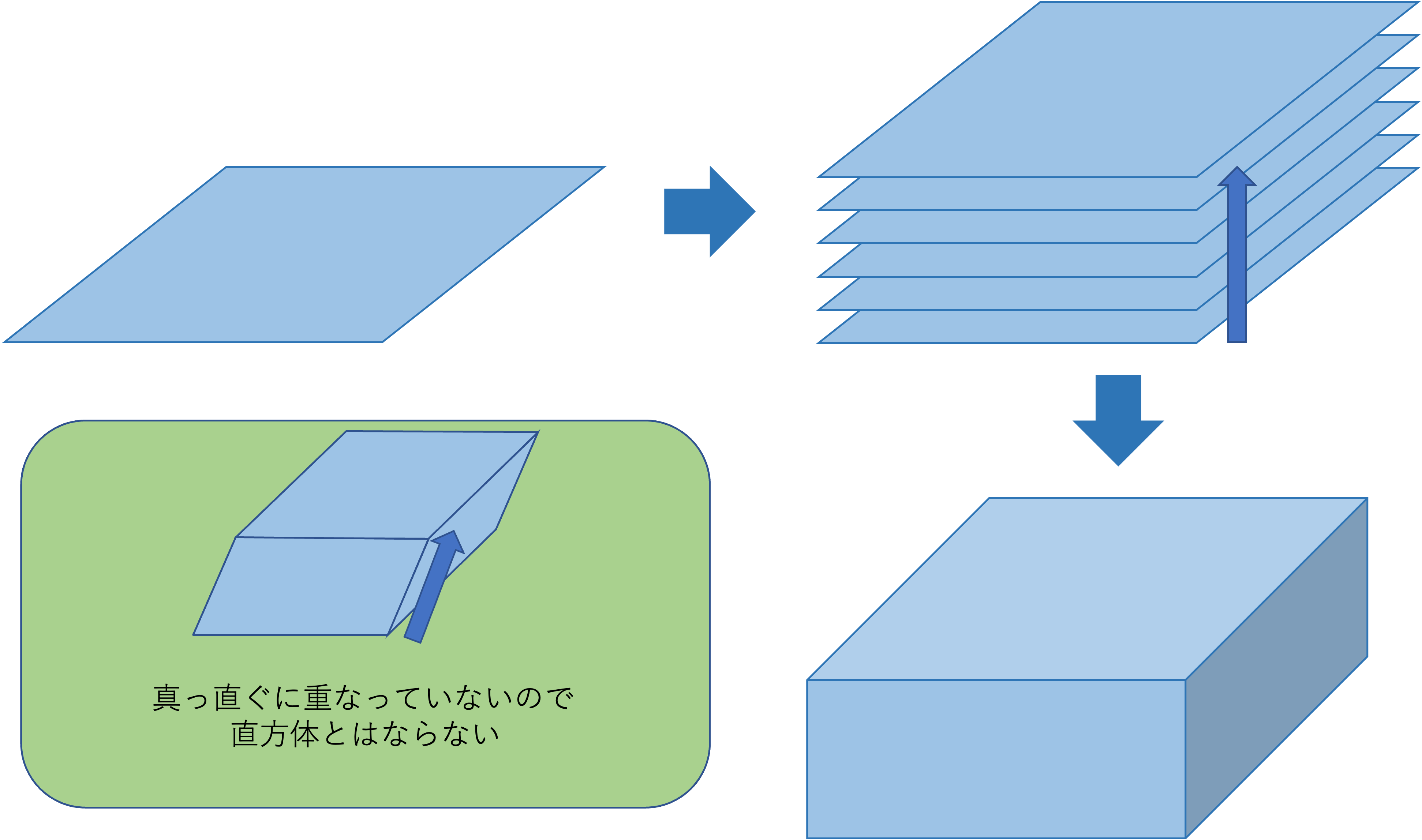
イメージとしては、まず初めに平面上にある長方形を考えて、その長方形を「高さ」の方向に重ねて（伸ばして）いくことを考えてみてください。

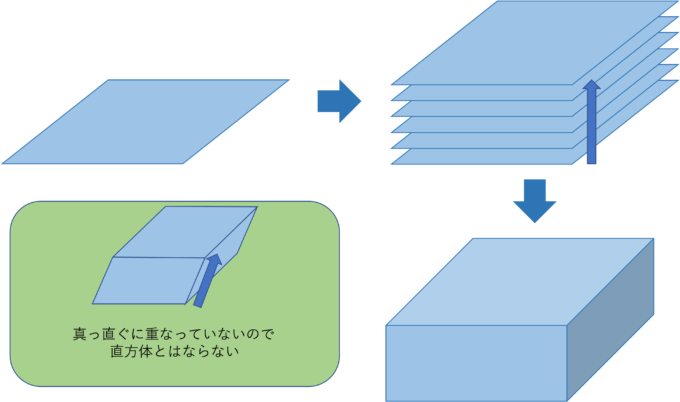
身近で分かりやすい例としてはお菓子やティッシュの箱や本などが挙げられます。
この時注意しなければならないのは、真っ直ぐと真上に重ねていかないと周りの図形が長方形にはならないので、直方体にはならないことです。

空間図形に関する言葉

ここで直方体を例に空間図形についての用語を確認していきます。
ここでは「頂点」、「辺」、「面」について確認していきますが、基本的なイメージは平面図形での意味と同じなのでざっくりと説明したいと思います。
まず、頂点とは文字通り空間図形で尖って「点」になっている場所のことです。
次に、辺とは頂点同士が結ばれてまっすぐな線分になっている場所のことです。
最後に、面とは辺に囲まれている多角形のことです。
直方体であれば頂点は8個、辺は12個、面は6個になります。

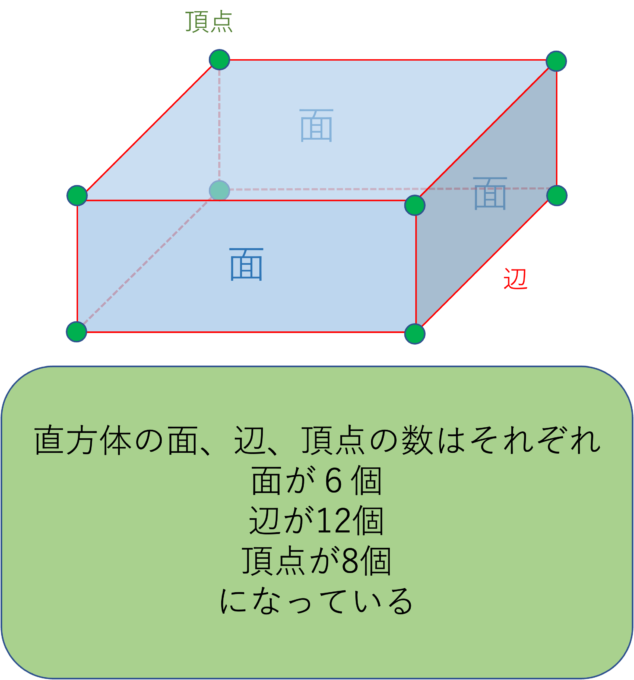
立体を書くときは、このように実際に見えない線を点線で書くと面や辺、頂点などの位置がわかりやすくなります。

立方体について

直方体がすべての面が長方形（正方形を含む）であるようなものだったのに対して、立方体とは、すべての面が（同じ形の）正方形であるような立体（直方体）のことです。

一番分かりやすい例はサイコロやルービックキューブなどです。
立方体は直方体の特別なものと考えられ、長方形や立方体のようにすべての面がすべて平面であるような立体を多面体と言います。

直方体や立方体の活用例

直方体や立方体のようにすべての面が平面であるような立体を多面体と言いましたが、特に立方体のような“形が綺麗”な多面体を正多面体と言います。
実は、この正多面体はどんなに頑張っても立方体を含めて５種類しか作れないことが知られています。
この事実は、「オイラーの多面体定理」と呼ばれる多面体についての定理から導き出されるのですが、この定理に関係するオイラー数と呼ばれるものについて考えれば、多角形だけでなくより多くの図形に対して同じような考えを適用することができることが知られています。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

座標（平面）とは【算数からやさしく解説】

<文/尾崎>