はじめに

大人のための数学教室和(なごみ)の講師の松中です。最近印象に残った授業シリーズとして不定期に授業の内容を紹介していきたいと思います。今回紹介したいのは2つの円の位置関係の条件に関してです。

なおこちらの記事の内容は動画でも解説しています。

2つの円の位置関係

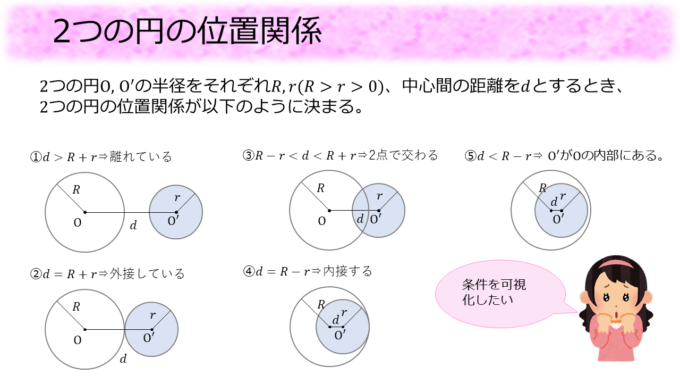
先日高校数学の授業で2つの円の位置関係についてお話ししました。大きさの違う2つの円はそれぞれの半径\(R\)、\(r\)、と中心間の距離\(d\)という3つの変数の関係により、

• ①\(d>R+r\)⇒ 離れている
• ②\(d=R+r\)⇒ 外接する
• ③\( R-r < d < R+r \)⇒ 2点で交わる
• ④\(d=R-r\)⇒ 内接する
• ⑤\(d < R-r\)⇒ 一方が他方の内部にある

のいずれかの位置関係になります。(大きさが同じ円の場合は「内接する」、「一方が他方の内部にある」の代わりに「一致する」という関係が現れます。)

これらの条件は図から明らかだろうと思いますが、何ともごみごみした条件達です。わかりやすく整理する方法はいろいろありそうですが、授業の中でこの条件を猛烈に可視化したくなりました。授業はそのまま続けましたが、授業後にDesmos上で可視化してみると、面白かったので紹介したいと思います。

3次元\((R,r,d)\)で可視化(GeoGebra)

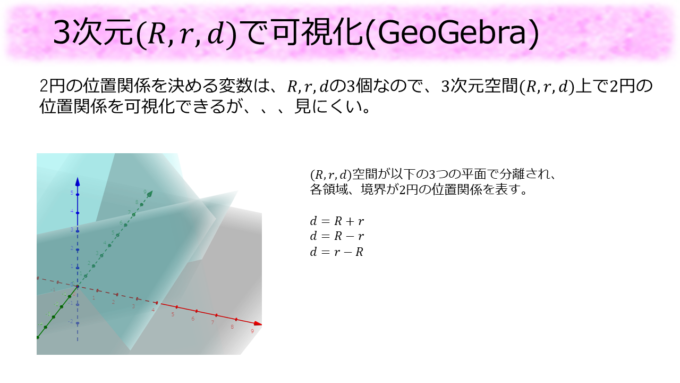
可視化をする上で最初に考えたのはGeoGebraという数学のソフトを使って、\((R,r,d)\)の3次元空間上で円の位置関係を表すことでした。条件から2つの円の位置関係は\((R,r,d)\)空間内の3平面、\(d=R+r\)、\(d=R-r\)、\(d=r-R\)で区分けされる領域や境界面で分類されることがわかります。しかしながらどうも見にくく諦めました。

2次元\((R,r)\)で可視化(Desmos)

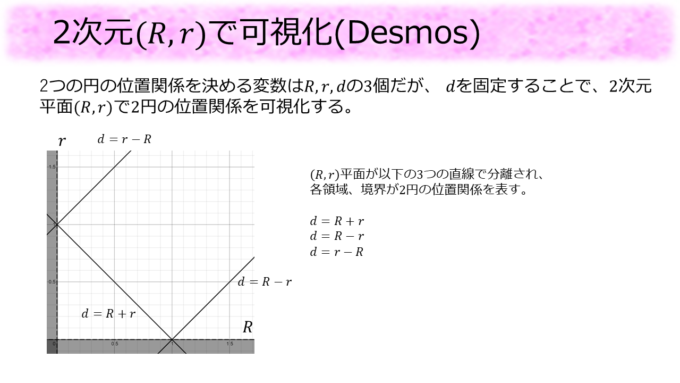
ということで3次元はあきらめて、2次元で可視化することにしました。3次元を2次元にするために\(d\)を\(d=1\)と固定しました。こんなことしてよいのかと思う方もおられるかもしれませんが、写真に2つの円が写っているときに、その写真を拡大、もしくは縮小すれば中心間の距離を\(1\)とすることができることがわかると思います。つまり、\(d=1\)と固定してもどんな2つの円の位置関係も表すことができるのです。

さて、\((R,r)\)平面で位置関係を分類する境界は3直線、\(d=R+r\)、\(d=R-r\)、\(d=r-R\)になります(\(d\)を固定しているので直線になります)。\(d=1\)として、これらを\((R,r)\)描画しました。\(R > 0\)かつ\(r > 0\)の領域はこの3直線によって4つの領域に区分けされますが、各領域と、境界上の点がどの位置関係を表しているかを見ていきましょう。、

位置関係の分類

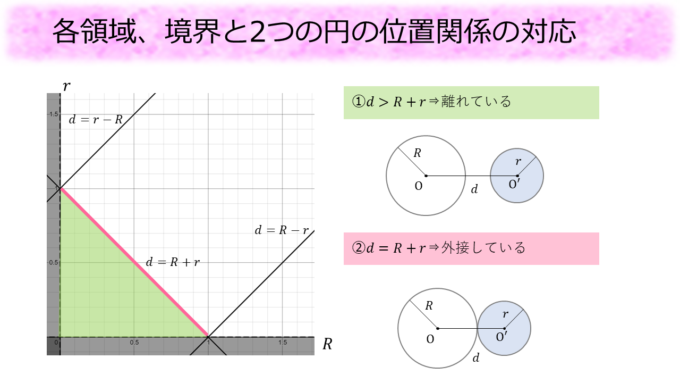
まずは、「①\(d>R+r\)⇒離れている」ですが、これは\(r < d-R\)となるので、図の緑の領域になります。そして「②\(d=R+r\)⇒ 外接する」は\(r=d-R\)ということで、図の濃いピンク色の線分上(境界上)となります。

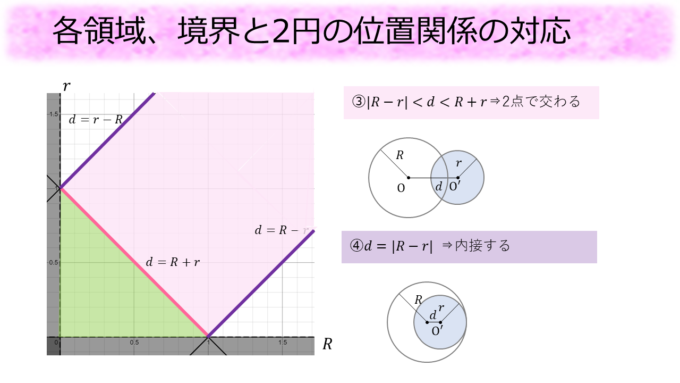
次に、「③\( R-r < d < R+r \)⇒ 2点で交わる」ですが、今は一般に\(R > r\)とは限らないため、これを\( |R-r| < d < R+r \)と書き換えます。\(R-r\)の正負によって丁寧に場合分けしてやれば、この不等式が表す領域は図のピンクの領域になります。さらに、「④\(d=R-r\)⇒ 内接する」も\(d=|R-r|\)と条件を書き換えることで図の2つの紫色の線分上(境界上)となることがわかります。

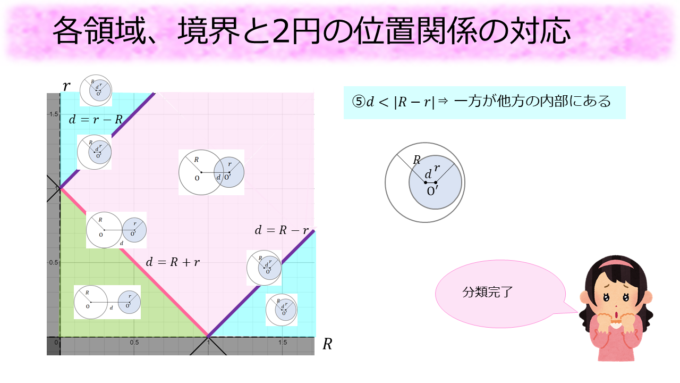
最後に、「⑤\(d < R-r\)⇒ 一方が他方の内部にある」も\(d < |R-r|\)と書き換えた上で、\(R-r\)の正負によって場合分けすることで図の水色の領域になることがわかります。 こうして\((R,r)\)平面上で2つの円の位置関係が完全に分類されました。

Desmos上でインタラクティブに可視化

Desmos上で\((R,r)\)平面に点を用意し、その点の位置に連動して2つの円の半径が変わるようにすると、分類通りに円の位置関係が可視化されたのでとても面白かったです。

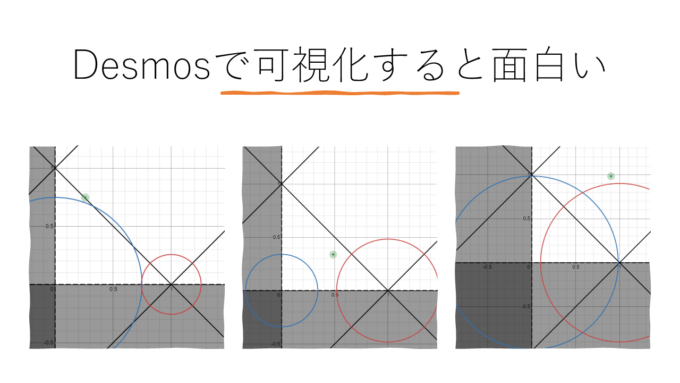
実際に触ってみてください↓

まとめ

高校数学にはいろいろな公式、問題が出てきますが、GeoGebraやDesmosで可視化すると面白いですよ。

円の方程式や、不等式が表す領域を詳しく学びたい方はこちらの講座がおすすめです。

図形と方程式

(文/松中)