微分を行列で表す~最近印象に残った授業~
公開日
2022年4月1日
更新日
2022年4月1日
この記事の主な内容
はじめに
大人のための数学教室和(なごみ)の講師の松中です。最近印象に残った授業シリーズとして不定期に授業の内容を紹介していきたいと思います。今回紹介したいのはベクトル空間に関してです。
なおこちらの記事の内容は動画でも解説しています。
微分は線形写像であり、行列で表すことができる

先日線形代数の体験授業がありました。線形代数と言えば行列式を計算したり、対角化したりと計算が多いイメージがあり、大学でも計算を主として講義される場合も多いですが、その体験授業ではお客様と相談し、線形代数の抽象的な一面について解説することになりました。(私は具体的な計算も嫌いではないですが、抽象的な数学が大好きでこの体験授業が印象に残りました。)
線形代数の主役となるベクトルとして普通は、数が並んだ数ベクトルや、高校で学んだ矢印(幾何ベクトル)が思いつくかと思います。しかし、抽象的に線形代数を学ぶ際は、ベクトルというのはベクトル空間の元のことであり、ベクトル空間には数ベクトルや矢印の集合だけではなく実に様々なものがあるのです。
ではベクトル空間とは何かというと、上で書いてあるような8つの条件をみたすような集合と演算の組のことです。この記事ではそこには深入りしません。
では数ベクトルや矢印の集合以外にどのようなベクトル空間があるのでしょうか。

実は変数\(x\)の\(2\)次以下の多項式全体も、中学や高校でやってきた足し算や実数倍を考えることでベクトル空間になります。体験授業の中ではこの集合がベクトル空間になることを確認しつつ、基底を考えてもらったり、このベクトル空間の次元を考えてもらったりして授業を進めていきました。
ちなみに基底の例として、一番わかりやすい\(\{1,x,x^2\}\)が挙がりました、また次元は基底に含まれるベクトルの個数で定義されるため、このベクトル空間の次元は\(3\)であることもわかりました。
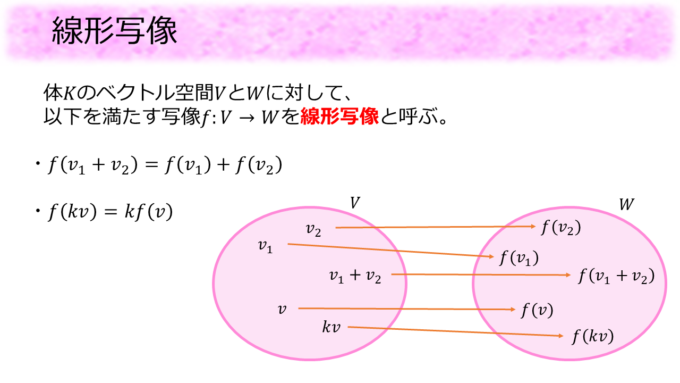
次に線形写像についても解説しました。線形写像とはざっくり、
\[
f(v_1+v_2)=f(v_1)+f(v_2)
f(kv)=kf(v)
\]
が成り立つような写像のことです。
普通の数ベクトル\(x,y\)と行列\(A\)、実数\(k\)に対して、
\[
A(x+y)=Ax+Ay\\
A(kx)=k(Ax)
\]
が成り立つので、計算がメインとなる授業では「線形写像=行列」というイメージがあるのですが、抽象的なベクトル空間では線形写像としてどのような例があるのでしょうか。
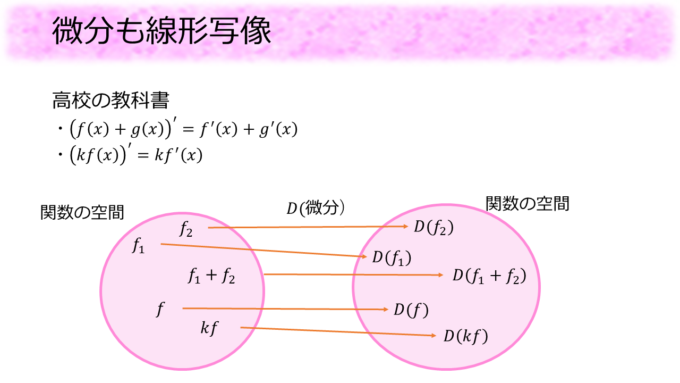
実は微分も線形写像なのです。高校の教科書には微分の公式として
\[
((f(x)+g(x)){\prime}=f^{\prime}(x)+g^{\prime}(x)\\
(kf(x))^{\prime}=kf^{\prime}(x)
\]
が載っていたと思います。
この微分を表す記号\(\prime\)を\(D\)という写像で表してみると、この公式は、
\[
D(f+g)=D(f)+D(g)\\
D(kf)=kD(f)
\]
を表していますね。これこそまさに線形写像が満たすべき2条件になります。
この微分という線形写像は関数の空間から関数の空間への写像として定義されています。この関数の空間というのはざっくりいうと無限次元のベクトル空間になります。このあたりは関数解析という大学数学の分野で学ぶ話になります。
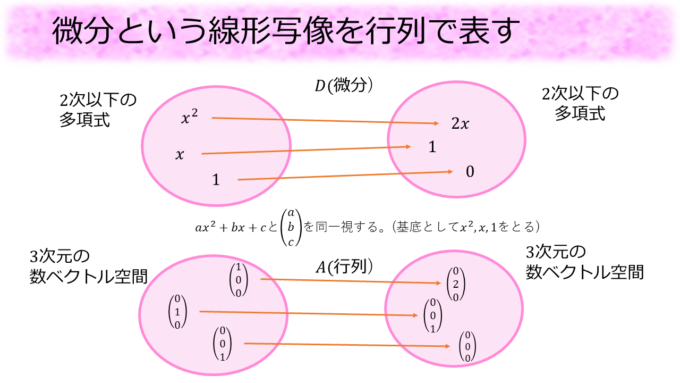
さて微分が線形写像であるということがわかったのですが、この微分を行列で表してみたいと思います。というのも、どんな抽象的なベクトル空間でも基底を定めることで同じ次元の数ベクトル空間と同一視することができるので、数ベクトル空間の世界で対応する線形写像を考えることによって元々の線形写像を行列で表すことができるのです。
今回の授業では2次以下の多項式からなるベクトル空間に\(\{x^2,x,1\}\)という基底を定め、2次以下の多項式\(ax^2+bx+c\)を数ベクトル\((a,b,c)\)と同一視することにしました。
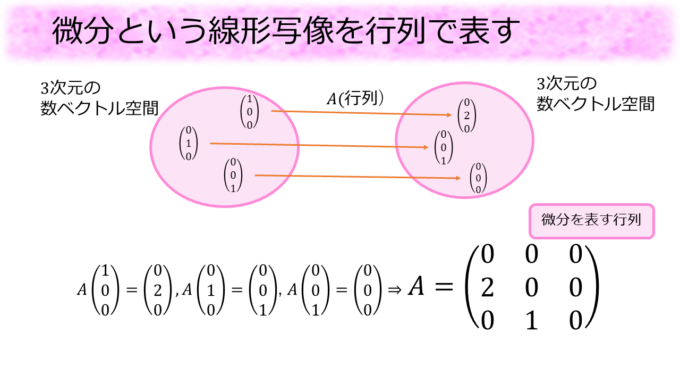
このように\(2\)次以下の多項式からなるベクトル空間と\(3\)次元の数ベクトル空間を同一視することで、微分を行列で表すことができます。
\(x^2\)の微分が\(2x\)に、\(x\)の微分が\(1\)に、\(1\)の微分が\(0\)になることから、この微分という線形写像は数ベクトル空間では、
\[
\left(
\begin{array}{c}
1 \\
0 \\
0\end{array}
\right)
\rightarrow
\left(
\begin{array}{c}
0 \\
2 \\
0\end{array}
\right)\\
\left(
\begin{array}{c}
0 \\
1 \\
0\end{array}
\right)
\rightarrow
\left(
\begin{array}{c}
0 \\
0 \\
1\end{array}
\right)\\
\left(
\begin{array}{c}
0 \\
0 \\
1\end{array}
\right)
\rightarrow
\left(
\begin{array}{c}
0 \\
0 \\
0\end{array}
\right)
\]
のように数ベクトルを変換することがわかります。この事実からこの微分を表す行列\(A\)は、
\[
A=\begin{pmatrix}
0 & 0 & 0 \\
2 & 0 & 0 \\
0 & 1 & 0
\end{pmatrix}
\]
となることがわかります。
今回は2次以下の多項式からなるベクトル空間の基底として\(\{x^2,x,1\}\)を選びましたが、別の基底を選ぶと微分を表す行列も変化することは注意してください。

上の計算例からも確かにこの\(A\)が微分を表していることがわかりますね。

なお、この行列\(A\)の\(2\)乗である\(A^2\)は2階微分を表す行列であることが分かります。実際に具体的な多項式で\(2\)階微分になることを確かめてみてください。
同様に\(A^3\)は3階微分を表す行列になりますが、これは計算すると零行列になります。これは、今考えているベクトル空間は2次以下の多項式からなるベクトル空間なので、3階微分をすると全て\(0\)になってしまうことを表しています。面白いですね。
まとめ

今回は少し抽象的なベクトル空間の話をしました。抽象的な線形代数の世界には数ベクトル空間以外のベクトル空間もたくさん出てきます。それでも基底を定めることでそれらのベクトル空間は数ベクトル空間と同一視でき、今回紹介したように線形写像は行列で表せます。そういった意味で、大学で学ぶ計算が主の線形代数もとても大事であるということをお伝えしたいと思います。
大学の線形代数を学んでみたい方には以下の講座がおすすめです。
(文/松中)














