円周率は３でよくないか問題

皆さんこの写真知っていますでしょうか。

そうパイなんですね。

パイと言っても、食べる方のパイではなくて円周率の方のパイですね(笑)

今回はこのパイについての話をしていきたいと思います。

この円周率というのはみんなからめちゃくちゃ愛されているわけです、

もう愛に満ち溢れてますよね(笑)

私の会社は、和から株式会社と言いまして、大人のための数学教室というものをしているんですけれども、なんと私の会社の資本金の金額は、こちらになってるんですね。(3,141,592円)

皆さん見たことありますよね。

そう円周率です、3.141592という形で非常にうまい金額になってる訳ですね。

素晴らしい良い金額ですよね！

さて、この円周率について結構話題になるのは、円周率は何で3ではいけないのかというものです。3で教えてるんじゃないか、いや教えてないよといったものが結構教育業界だと何度か話題になってるんですよ。なので、今回はこちらの問題について触れていきたいと思います。

まず、円周率って3じゃいけないのかと言われると

「実は別にいいんじゃないですか？」

というのが結論になります。3でもいいと思うんですよね。

3じゃ明確に駄目な理由ってなんなんだろうというのを考えてみると、

「別にダメっていうわけではないと思いますけど……」

というのが何となくの結論になってきます。

別に3でも悪くはないと思うんですよね。

円周率の誤差を考える

円周率の表現方法は、3という風に表現する場合と、3.14という風に表現する場合があります。

でも、円周率って正確な値って何かって言うと、3.14159265358979…という形で無限に続くような。しかも、循環しないような少数がずっと続く値。

これが正確な値なんですよ。なので、3.14でも間違ってるんですね。

だから、3でも間違えているし、3.14でも間違えているんですよ。

つまり、我々が議論すべきなのって何かと言うと、誤差をどのぐらい許容しますかというところに対してちゃんと議論をすべきだと思うんですよね。

「誤差」です。

議論すべきは、3.14だと不正確、3だと不正確という話ではなくて、「誤差をどこまで認めますか？」というところをきちんと決めなきゃいけないと思うんですよ。

そもそも円周率の定義とは何かと言うと、円周の長さを直径の長さで割った値という風になってます。

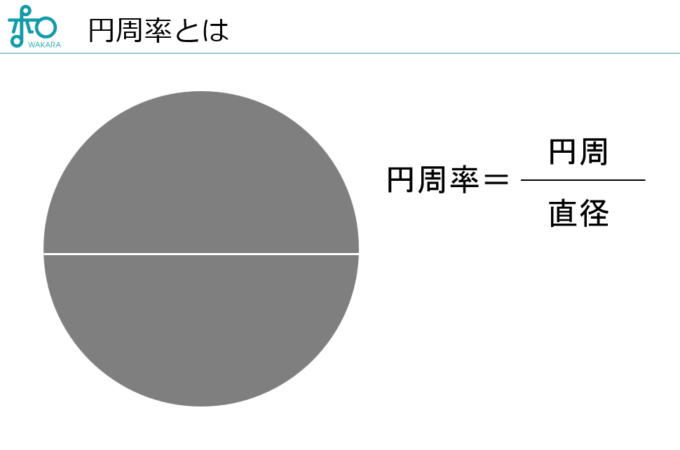
直径の長さの何倍が円周の長さになるのか。この”何倍”のところが実は円周率になっているんですね。つまり、直径の長さの三倍ぐらいの長さが円周の長さということになります。

実は、この円周率を仮に3と置いてしまった時に何が起こるのかというと、まず、内接する正六角形がありますよね、この正六角形の外周の長さは直径の長さが1だった時に3になる訳なんです。

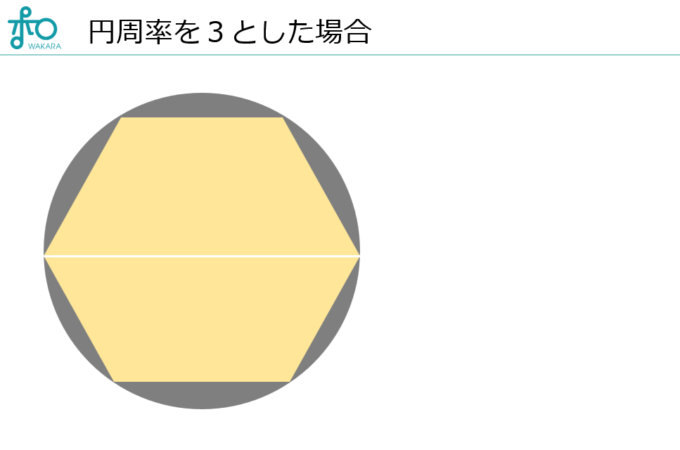
なので、全然違うといえば違う訳です。

ぱっと見て違いが判りますよね。

車や自転車のタイヤを正六角形のタイヤで回しますって言ったら、

全然違うカクカクでガクガクガクガクする車になってしまう訳なんです。

全然うまく走らないってことになってしまうんですね。

人との会話では、誤差は大幅に許容される

そういう意味では全然違うんですが、人との会話で円周率3っていうのが許容できるかどうかっていう話をすると…

例えば、買い物をしたときに、9,500円の買い物をしたとして、人に話す時にざっくり「この間1万円ぐらい買い物したんだよね」って話をしたときにこれは嘘になりますかという話なんですよ。

嘘ではないですよね。

ざっくり1万円の買い物をしたよというので合ってるじゃないですか。

だから、人との会話の中で誤差5％ぐらいのちょっとした誤差があるような会話とかは結構許されたりするんですね。

当たり前のことを言ってますけど、この当たり前のことを確認していくことっていうのが凄く大切になってきます。

人との会話の中であれば、誤差が多少あったとしても全然許しちゃうんですよ。

でも、ちょっと待ってください。

建築あるいは宇宙にロケットを飛ばすとか言ったときに誤差を本当に許容できますかと言うと、

例えば、100mのビルを立てようとしてるのに105mの長さで建ててしまったと言うのはおかしいじゃないですか。

そうなると、全然誤差を許容できないということになります。

ここで知っておきたいのが、実は、正確な円周率πの値と3の間には誤差が5％ぐらいあるということです。

なので、この5％というのをどのぐらい許容できるのか、というのをきちんと捉えなければいけないんですね。

人との会話に中において誤差5％っていうのは普通に起こり得る問題です。

つまり、図で表すとこんな形になりまして、

円周率の正確な値が一番下の値ですね。

これに対して、円周率を3とすると誤差がざっくり5％ぐらいです。

また、3.14って言ってしまったとき、実はこれも間違いなんですよ。

つまり、3.14もそもそも許されるのかどうかというのをきちんと議論をすべきなんですよね。

実際に誤差を測ってみると、誤差が0.05％発生します。

だから正確には3.14でも駄目なんです。

この0.05％というのは大体二千分の一ぐらいです。

二千分の一というのは、100mのビルを立てるときに誤差が大体一万分の五という形なので、5cmぐらいずれるよってことです。

5cmと聞くとそんなでもないかなという風に感じるかもしれないですが、100mのビルを建てた時に窓が5cm空いてますと言ったら全然大きな問題じゃないですか。

つまり、わずかな誤差でも許されないことがあったりするわけです。

なので、3.14でも正確には間違っていて、これで計算するのは本当にいいんですかと言ったら、正確に計算しなきゃいけない場面ではやはり駄目なんですよね。

例えば、小学生にはやぶさを着陸させますと言った時に、「それは3.14で本当にうまく着陸するんですか」という話なんですよ。

さらに不正確なこと言うと、例えば、友人に2000件ほどLINEを送るときに、一通ぐらいは間違えて他の人に届きますとなったら嫌じゃないですか。

だから、やっぱり二千分の一でも誤差が許されないことというのがある訳ですよ。

そう考えたら誤差を許して大体3ぐらいだよっていう風に捉えて、あとは正確な値というのは無限に続くし、3よりも大きいということを念頭に置きながら円周率について向き合っていくことが凄く大切なのかなと思います。

何よりですね、私の会社の資本金が3.141,592円なので、このぐらいの桁までは覚える教育であってほしいなと思っています(笑)

最終的な結論としては、誤差を許容するのであれば円周率を3としても問題ないということで今回の動画のお話をさせていただきました。

ということで、少しでも円周率の楽しさについて感じていただけたんなら幸いです。

もし面白ければチャンネル登録といいねボタンのクリックをぜひよろしくお願いいたします。

また、是非コメントで感想なども聞かせていただければ幸いです。

最後までご視聴いただきありがとうございました。

　

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/堀口智之>