動画で見たい方はこちら↓↓↓

こんにちは。和からの数学講師の岡本です。以前、素因数分解のゲーム「Prime Smash!」に関する記事を書いた際、「どうすれば素数かどうか判定できるの？」という声をたくさんいただきました。

Prime Smash!～素数マスターへの道～

与えられた整数が素数かどうかを判別する方法はそんなに簡単ではありませんが、「何かの倍数」かどうかを判別する方法はいくつかあります。例えば、「31932」のように1の位の数が偶数であれば、どれだけ大きな数であろうと、偶数なので2で割れることがわかります。他の数はどうでしょうか？詳しく見ていきましょう！

1) 5の倍数判定

まずは「5の倍数」かどうかの判定法をご紹介します。これは、非常に簡単で、1の位の数が「0」もしくは「5」であれば、その数は５で割れます。例えば、5×偶数は１の位は必ず「0」になります。「5×4=20,5×8=40」というように、感覚的には理解できるかもしれませんが、ここでは式を使って証明してみましょう。例えば、「偶数」というのは、整数\(n\)を使って\(2n\)と表すことができます。そのため「5×偶数」は

\begin{align*}
5\times 2n=10n
\end{align*}

となり、整数\(n\)×10という形から、1の位の数は必ず「0」であることがわかります。また、同様に「5×奇数」を考察してみましょう。「奇数」というのは、整数\(n\)を使って\(2n+1\)という形で表すことができます。そのため、「5×奇数」は

\begin{align*}
5\times (2n+1)=10n+5
\end{align*}

となり、1の位の数は0である数に5が足されている形をしています。したがって、1の位の数は「5」であることがわかります。全ての整数は偶数か奇数かしかないので、5の倍数は1の位が「0」か「5」の2通りであることがわかりました。

2) 3の倍数判定

続いては今回のメインである「３の倍数の判定法」をご紹介します！これは意外と便利なので知ってて損はないと思います！たとえば「1122」という数は3で割れるかどうか瞬時に判断できますか？九九で出てこない大きな数なので、割り算をして確かめるのは少しめんどくさいですよね。しかし、判定法を知っていれば、この数が「３の倍数」であることが瞬時にわかります！

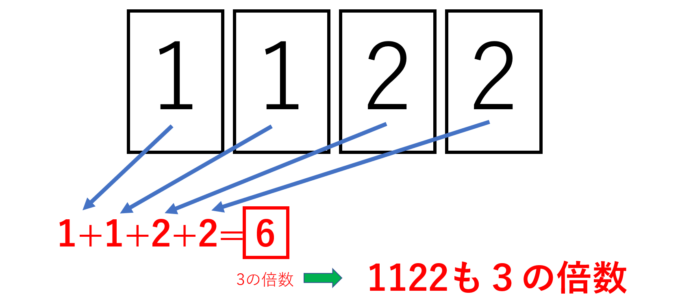
なんということでしょう…。実は各桁の数を足すだけで、3の倍数かどうかがわかるのです！実際に「1122」の各桁を足すと「1+1+2+2=6」となり、3の倍数です。このことから「1122」も3の倍数であることがわかります！超便利ですよね！

「12341」はどうでしょう？各桁の和は「1+2+3+4+1=11」なので3の倍数ではありません。つまり、「12341」は3の倍数ではありません！「393」はどうでしょう？お気づきかもしれませんが、各桁の3の倍数だと、足しても3の倍数になるので「393」は明らかに3の倍数であることがわかります。では「31932」を見てみましょう。桁数も多く、足し算が面倒に見えますが、5個の数の内3つが3の倍数なので、3の倍数ではない「1」と「2」だけに注目すればいいのです。

なお、「1+2=3」なので、「31932」は3の倍数であることがわかります。すごい破壊力ですね！

3) さいごに

いかがでしたでしょうか？「2の倍数」「3の倍数」「5の倍数」までは、実は比較的すぐに判断できます。素数かどうかを判断する際、最低限2でも3でも5でも割り切れないことが条件ですから、まずは今回のような判定を瞬時に行います。なお、今回は3の倍数の判定方法をただ紹介しただけですが、次回はキチンと数学を使って証明してみようと思います。メカニズムがわかって使うとなお気持ちがいいと思います！次回もお楽しみに！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>

藤子・F・不二雄作品シリーズ 11 バイバイン