こんにちは。和からの数学講師の岡本です。今日は統計やデータ分析で最近よく話題になる「四分位数」について紹介していきます。昔と違って、今では中学校や高校でも四分位数をしっかりと学習するようなので、押さえておくべき重要なトピックだと思います。

１．四分位数と箱ひげ図

まずは四分位数をシンプルに説明します。数値のデータを小さい順に並べ、これを4等分割します。そのときの最小の値から順に「最小値」「第1四分位数（25%点）」「中央値」「第3四分位数（75%点）」「最大値」と呼びます。

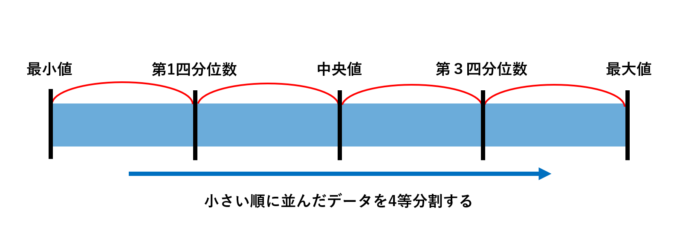
「第１四分位」と「第3四分位」の範囲を四分位範囲と呼び、以下のような「箱ひげ図」と呼ばれるグラフが作成できます。

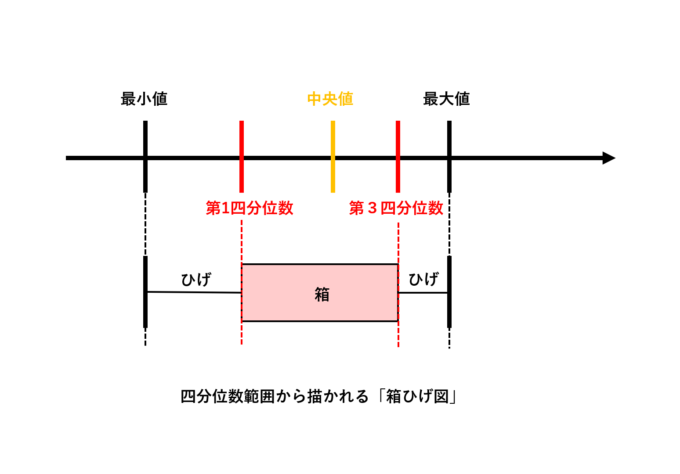
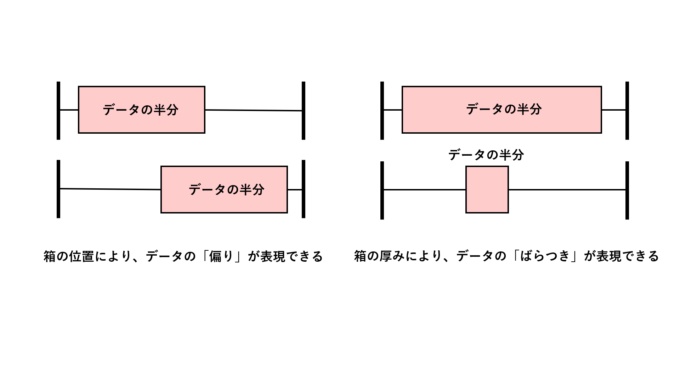
四分位範囲を「箱」とし、最大値、最小値に向けて「ひげ」をのばしたような形をしています。このグラフの読み方ですが、四分位範囲はデータの25%～75%をしめている範囲なので、言い換えると「中央値周りのデータの半分」が位置している範囲を表します。つまり箱の位置によって「偏り」が表現できるのです。また箱の厚みにも意味があります。例えば箱が薄ければ、データの半分が中央値付近に固まっていることを表し、箱が厚ければ、データの半分が中央値を中心に広くばらついていることを表します。つまり、箱の厚みにより「散らばり具合」も表現できるのです。こんなにもシンプルかつ分布の特徴をつかめるグラフは珍しいので、しっかり覚えておきましょう。

２．四分位数にはいくつも定義がある？

先ほど説明した四分位数についてですが、実はいくつか異なる定義があるようです。
１つは現在、学校の教科書に載っている“文部科学省推奨の四分位数”、もう一つは箱ひげ図考案者である“Tukeyのオリジナル四分位数”、そしてExcelやRで使われる、“計算機タイプの四分位数”です。
最大値、最小値、中央値はどれも同じですが、第1四分位数と第3四分位数が少しだけ違ってきます。違いの説明の前に「中央値」の定義について確認しておきましょう。
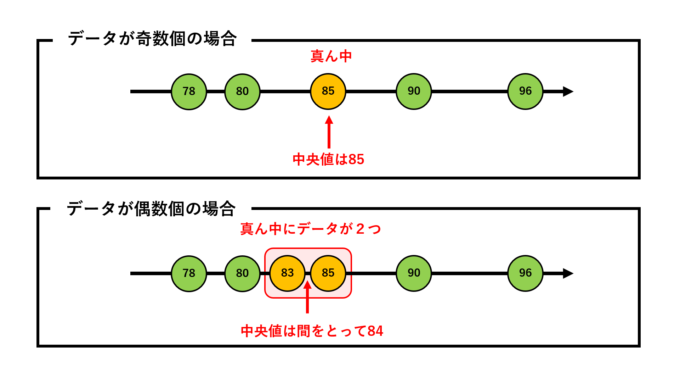
例えば「\(78, 80, 85, 90, 96\)」という5つのデータが小さい順に並んでいます。このデータの最小値は(78\)」、最大値は「\(96\)」です。そして真ん中（3番目）の数値である「\(85\)」が中央値となります。
しかし、データの個数が偶数個の場合、“真ん中の番号”がありません。例えば「\(78, 80,83,85, 90, 96\)」という6個のデータの場合、“真ん中”には「\(83, 85\)」という２つの数値があります。この場合、真ん中2つの数値の平均値つまり\((83+85)\div 2=84\)が中央値となります。

３．文部科学省推奨の定義

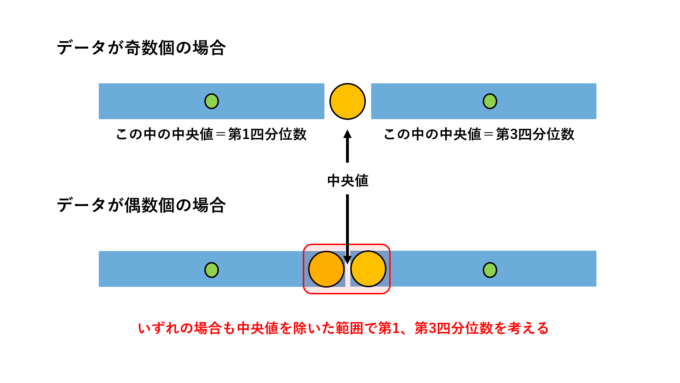
文部科学省の定めた教科書に載っている四分位数の定義を説明しましょう。まずデータを小さい順に並べ、中央値をとります。次に中央値未満のデータで中央値をとり、これを第1四分位数とします。また、中央値より大きいデータの中で中央値をとり、これを第3四分位数とします。つまり、第1と第3四分位数を考えるとき、真ん中の中央値を除いて考えるのが文部科学省推奨の定義となります。

４．箱ひげ図考案者Tukeyの定義

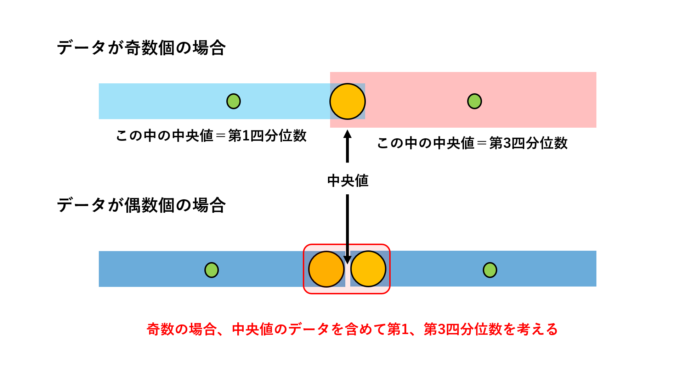
では、箱ひげ図考案者Tukeyの定義をみてみましょう。Tukeyは、文部科学省推奨の定義とは違い、中央値を含めて第1、第3四分位数を定めます。

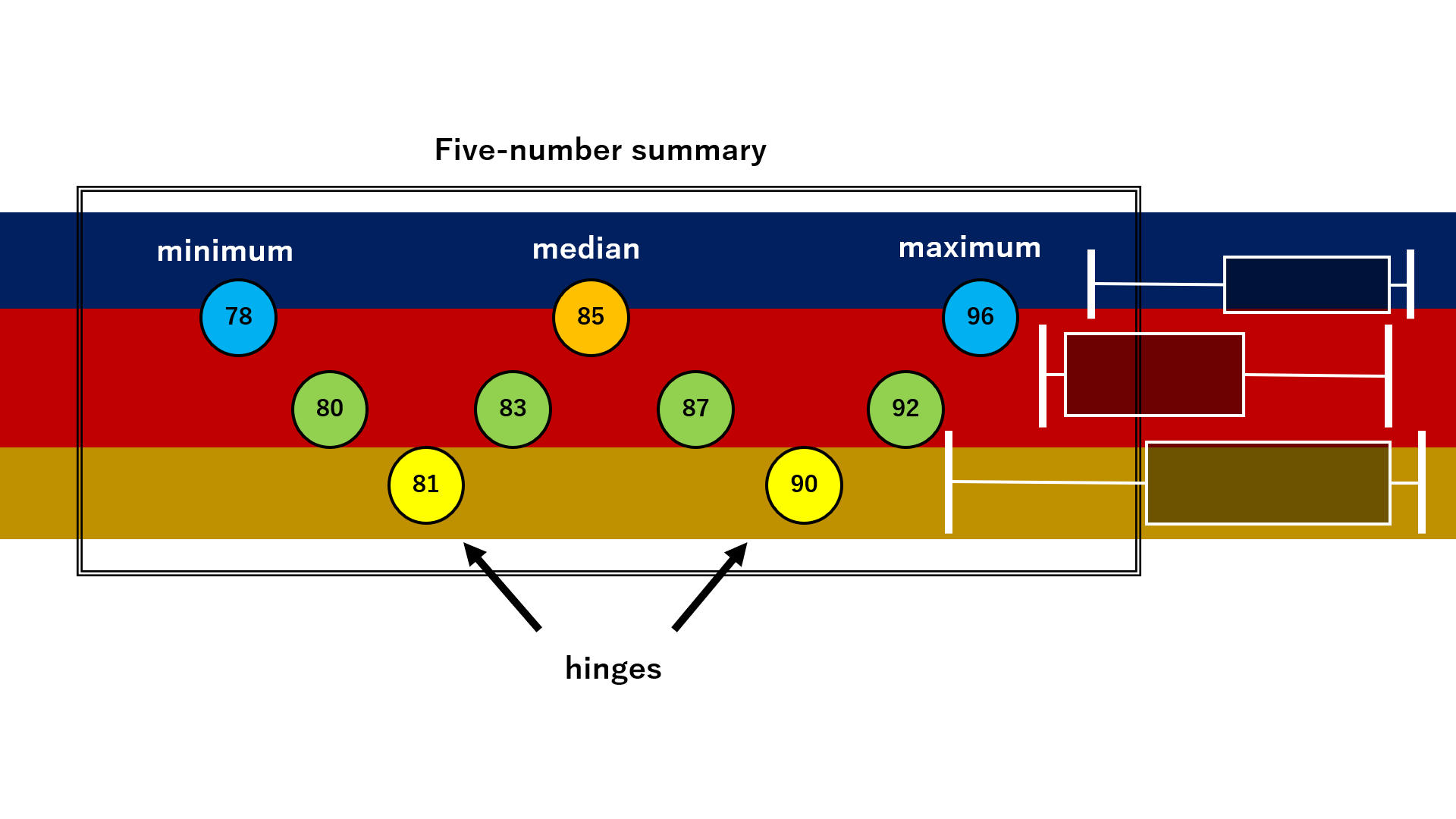
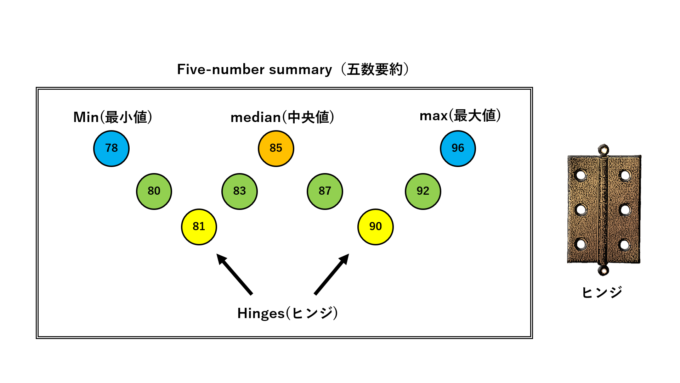
なお彼の論文では、第1、第3四分位数を「hinges(ヒンジ)」、最大・最小・中央値と合わせて「five-number summary(五数要約)」とよび、以下のような図で表現しています。なお、岡本はこの定義で授業を行っています。

５．Excelの定義

最後にExcelなどの計算機で定められている四分位数の定義を紹介します。例えばExcelの「QUARTILE.INC関数」について説明します（Rでは「quantile関数」。また、「fivenum関数」でTukeyの定義を使用できます）。大量のデータに対して効率よく機械的に計算できる仕組みが考えられており、冒頭に説明した「4等分割する」という考え方を忠実に計算しています。なお、「QUARTILE.INC関数」は「＝QUARTILE.INC(データ, 戻り値)」という具合に入力する必要があり、戻り値は「0：最小値」「1：第1四分位数」「2：中央値」「3：第3四分位数」「4：最大値」と対応づけられています。つまり、最小から最大まで全てQUARTILE.INC関数で表現できます。

計算の仕方はやや複雑ですが以下のようになっています。

①（データ数\(-1\)）に\(0.25\), \(0.5\), \(0.75\)を掛ける。
②その値が
【整数の場合】その番号のデータがそれぞれ第1四分位数,中央値,第3四分位数になる。
【整数＋0.25の場合】その数より１つ大きい数\(k\)と\(k+1\)番目の値で調整する。

\begin{align*}0.75\times x_k+0.25\times x_{k+1}
\end{align*}

【整数＋0.5の場合】その数より１つ大きい数\(k\)と\(k+1\)番目の値で調整する

\begin{align*}0.5\times x_k+0.5\times x_{k+1}
\end{align*}

【整数＋0.75の場合】その数より１つ大きい数\(k\)と\(k+1\)番目の値で調整する

\begin{align*}0.25\times x_k+0.75\times x_{k+1}
\end{align*}

６．さいごに

せっかくなので全部の場合をデータ数が偶数と奇数の場合で計算してみました。

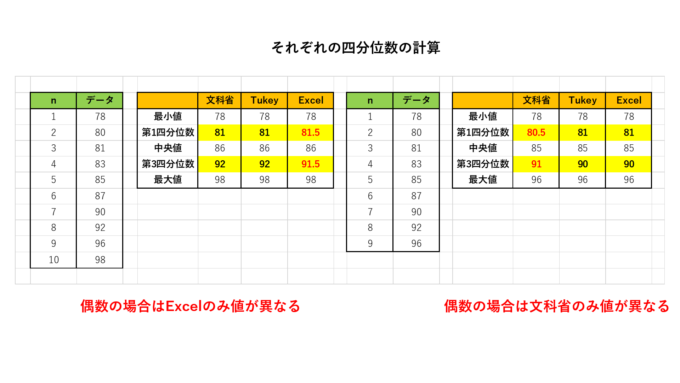
簡単な考察からわかりますが、データ数が偶数の場合、文科省推奨の計算とTukeyの計算は一致します。また、データ数が奇数の場合、Tukeyの計算とExcelの計算は一致します。結論としてはどの定義をとっても、ある程度大きな数のデータを扱う際はほとんど結果に差がでません。それに、そもそも四分位範囲の値は4分割したときの正確な数値が知りたいのではなくて、あくまでデータ全体を把握するために使う指標です。文部科学省が教科書にこのうち１つの定義だけ採用しているのは、単に一番簡単な定義だからだそうです。たしかにあまり複雑なものを押し付けるのも良くはないかもしれません。
とにかく、あまり数値に惑わされず、目的を明確にしてデータを要約していきましょう！
こうした統計学やデータ分析におけるデータの基本的な扱い方や捉え方に関して、和からでは無料のセミナーを実施しております！興味のある方は是非一度参加してみてはいかがでしょうか？

文系のための「統計超入門セミナー」-目で見てわかるビジネス統計学-

とりあえず、統計って何？

集計と可視化で学ぶデータ分析超入門

文系理系問わず、忙しい社会人にとって統計を勉強することはすごく難しく感じられますが、弊社のセミナーでは基本的に数式を使わずに要点をしっかりつかんでいただく内容となっています！どうせ勉強するなら「楽しく」学んでいきましょう！

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>