こんにちは。和からの数学講師の岡本です。今日は「人はなぜサボろうとするのか」というテーマでお話をしていきます。皆さんは「勉強」や「課題」、「仕事」などを一定の期限内に仕上げなければいけない場合、ついつい先延ばしにすることありませんか？（僕もあります。「夏休みの宿題」など…。）
先延ばしにすればするほど困るのは自分なのに、なぜサボるという選択肢を選んでしまうのでしょうか？なんだか数学っぽくないですが、実は数学を使って簡単なモデルを考えることができます！

１．「サボる」とは

まずは「サボる」という言葉について説明していきます。これは「仕事やタスクを怠る」という意味でよく使われます。しかし、語源となったのはフランス語の「サボタージュ（Sabotage）」で、元々は「破壊活動」を意味する言葉なんです！！ちょっと恐ろしいですね…。ある意味サボることによっていろんなもの（課題の質や時間、精神など）が破壊されていく感じは想像できますね。

２．数理モデル（コストと反比例）

例えば、1か月（31日）で仕上げなくてはいけない課題があるとしましょう。「課題をこなす」というのはある意味“コスト”です。そこで、この課題の総コストを仮に「31」とします。そうすると、1日平均「１」のコストで課題をこなせば、１か月後、無事に課題が完了します（これを「1日平均ノルマ」と呼ぶことにしましょう）。しかし、夏休みの宿題のように、「1か月もあるんだから、ちょっとぐらいサボってもいいだろう」という“悪魔の囁き”により、何日もサボってしまいがちです。では、1日サボった場合、課題の総コストは31のままですが、期間は1日減って30日となってしまいました。この場合、2日目の時点における1日平均ノルマは

\begin{align*}
\frac{31}{31-1}=1.033333\cdots
\end{align*}

となり、初日よりも大きくなっています。同様に\(x\)日間（\(0\leq x \leq 29\)）サボった場合、\(x+1\)日目における1日平均ノルマは

\begin{align*}
\frac{31}{31-x}
\end{align*}

と表すことができ、\(x\)の関数となります。1日平均ノルマ\(y\)をグラフにすると以下のような反比例型のグラフになります。

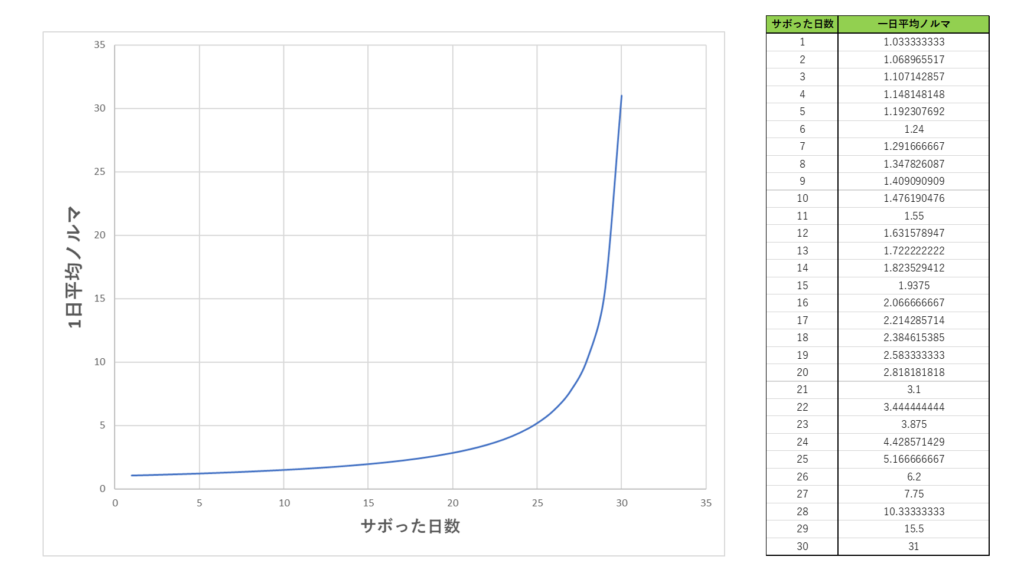
ご覧の通り、1日平均ノルマというものは直線的（比例関係）に増加ものではなく、反比例の関係により急に増加するのです！これが現実です…！

３．時間による「割引」という感覚

では、サボることにより1日平均ノルマは恐ろしく増加をするわけですが、それでも我々は「1日サボってもいいかな」という感覚を持ってしまいます。この感覚は「時間による割引」という概念で簡潔に説明できます。
例えば、今すぐに1万円もらえるのと、10年後に1万もらえるの、皆さんはどちらを選びますか？ふつうは今すぐもらえた方がいいですよね？これはある意味、時間が経過するにつれてものの価値が下がっていることを意味します。例えば、明日の1万円は現在において9,500円の価値に相当するといった具合に、前日の95%の価値に下がっていくモデルを考えます。すると2日後の1万円は現在において

\begin{align*}
10,000\times 0.95\times0.95＝9,025
\end{align*}

となり、9,025円の価値になってしまいます。この場合の「95%」という比率を「割引率」と呼ぶことにします。この感覚は「コスト」にも同様に当てはめることができます。

４．コストの時間割引によるサボタージュ発生

それでは、コストに関しても「時間割引」というものを考えていきましょう。つまり、「今日支払うコストよりも明日のコストの方が価値が低い」という考え方です。
具体的に、1日サボった場合、1日平均ノルマは1.0333…と、1より大きくなるのですが、割引率95%で考えると、翌日の1日平均ノルマは

\begin{align*}
1.0333\cdots \times 0.95=0.98166\cdots
\end{align*}

となり、感覚的に１よりも小さく感じられます。さらに、2日サボった場合、1日平均ノルマは客観的には

\begin{align*}
\frac{31}{31-2}＝1.06896\cdots
\end{align*}

となるのですが、時間割引により

\begin{align*}
\frac{31}{31-2}\times 0.95^2＝1.06896\cdots \times 0.95^2=0.9647\cdots
\end{align*}

となり、やはり１より小さく、感覚的には1日サボるよりも割安に感じてしまいます。恐ろしいですね…。実際の一日平均ノルマと、割引率95％を想定した感覚的な一日平均ノルマをグラフを作成してみました。

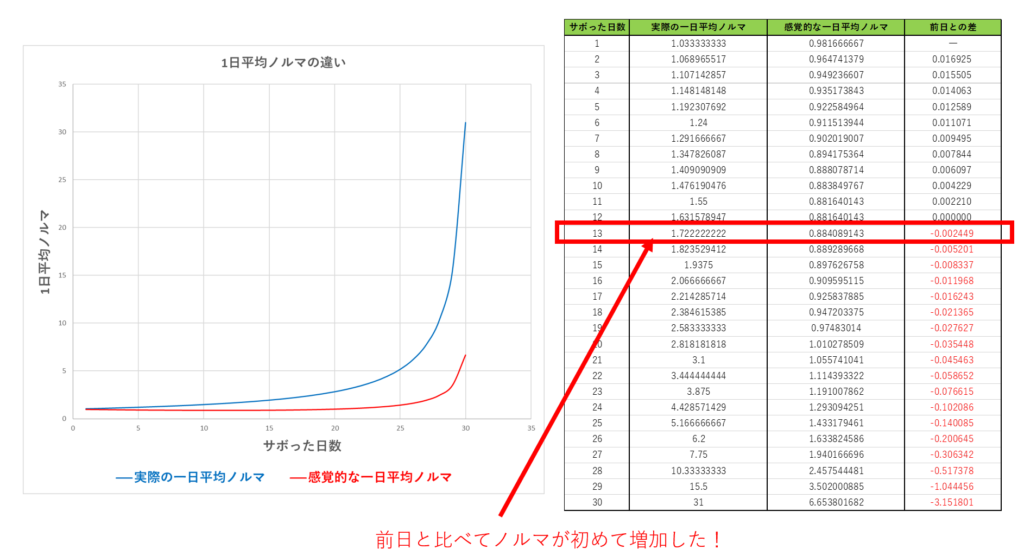
感覚的なノルマは10日以上、下がり続けます。一日平均ノルマが前日よりも上回ったとき、ようやく課題に取り掛かる。それが人間なのです（例えば私）。非常に単純なモデルですが、これが「サボる」という数学的な説明となります。ちなみに今回の設定では、13日サボってからようやく腰を上げるのですが、その時すでに実際の一日平均ノルマは1.7を超えています。

５．さいごに

いかがでしたでしょうか？時間によるコストの割引という感覚のため、我々は「サボる」という選択肢をついつい選んでしまいがちであることが簡単な数理モデルで説明できました。
しかし、今回のモデルは非常に簡潔なもので、最初に立てた計画が後から変わってくることじゃありません。これは今回のような指数関数型モデルの特徴です。ただ、どうしても「明日から本気を出す」という具合に次々に先送りにしてしまう感覚についてはもう少し別のモデルを利用することでうまく説明できます。このあたりの説明は以下の本で詳しく紹介されていますので是非ご覧ください。

その問題、数理モデルが解決します 浜田宏(著) ベレ出版

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/岡本健太郎>