こんにちは。和からの数学講師の岡本です。今日はつぎのような「ゲーム」について考えます。

参加者が20人いるとします。20人にそれぞれ番号を付け、図のように輪になって並んでもらいます。

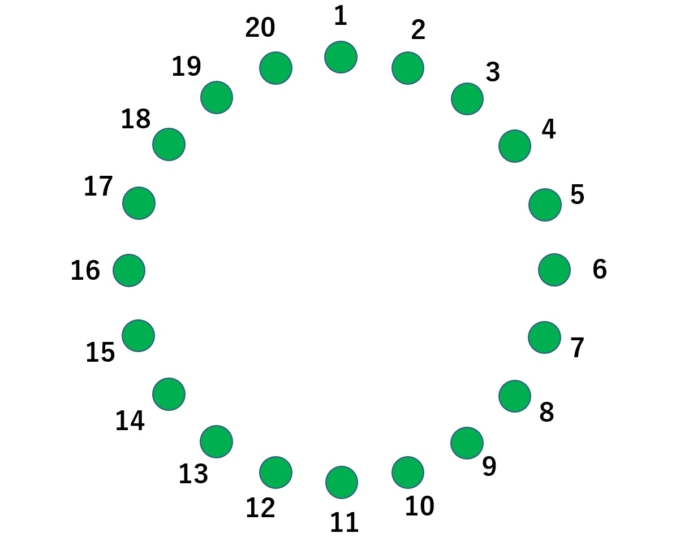
そして1番の人が座わり、そこから時計回りに「1つ飛ばし」で座ってもらいます。さてこのとき最後に残るのは何番の人でしょうか？10秒でお答え下さい！といっても難しいのでゆっくり考えていきましょう。

１．愚直に考えてみる

考察するときはまず、「愚直に試してみる」ことが大切です。20人が輪になっているとしましょう。1番から順番に3,5,7,…と、まずは奇数番号の人が座っていきます。1周回った時点で残っているのは20番までの偶数だけです。19番が座った後、「1つ飛ばし」のルールのもと、20番をとばして2番が次に座ることになります。そして、4番を飛ばして6番、10番といった流れです。一通りシミュレーションすると、どうやら残るのは8番のようです。

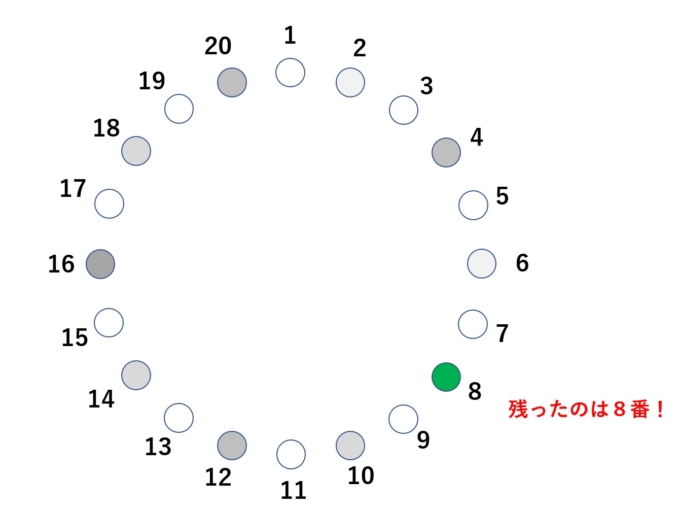
そこで考えます。「どんな仕組みで8番が残ったのか？」

２．簡単な具体例から攻める

複雑に見える対象のメカニズムを理解するための常套手段は「極端に簡単な例」を考えることです。そこでまず2人の場合を考えます。この場合、1番が座れば2番が残り、即終了です。次に4人の場合を考えます。

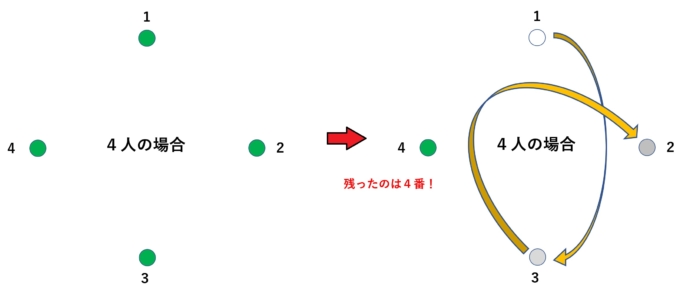
この場合、図のように1,3,2ときて残るのは4番です。次に8人の場合を考えましょう。

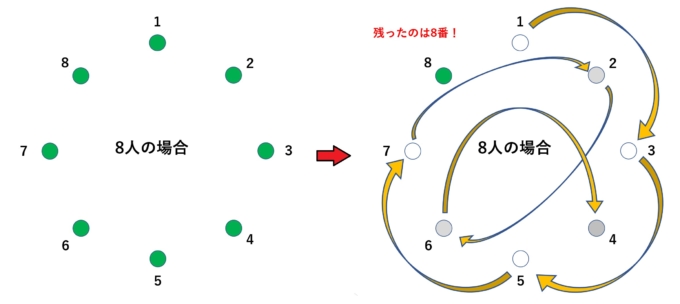
この場合も同様に観察すると1,3,5,7,2,6,4ときて、残るのは8番です。お分かりいただけましたでしょうか？このとき、注意して観察すると次のようなことがわかります。

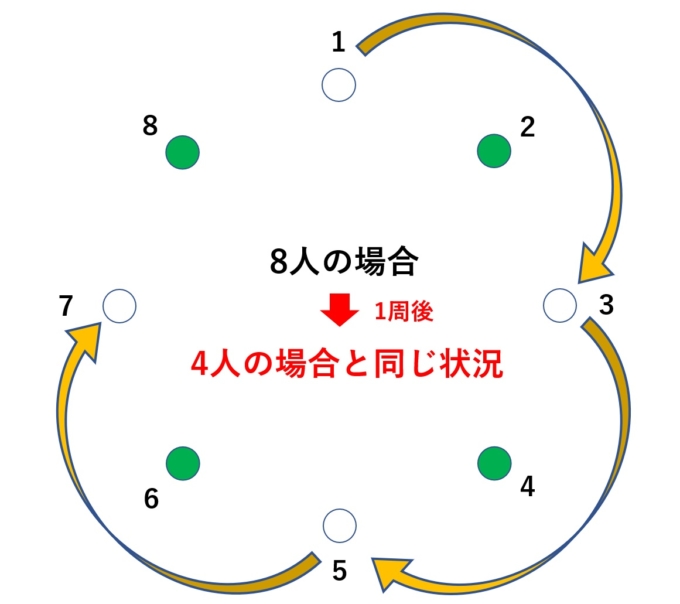
8人の場合、最初の1周で1,3,5,7が座ります。この時点で残っているのは2,4,6,8の4人です。つまり、4人の場合に帰着できるわけです。これは一般の2の冪乗人の場合にも同じことが言え、最終的には「スタート地点の1つ前」の番号が残ることがわかります。

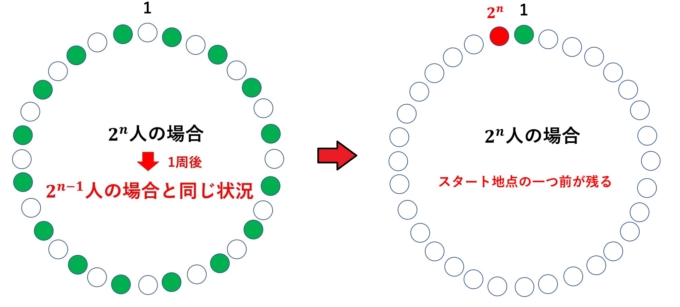
つまり、1番から座るルールであれば、8人のときは8番、16人のときは16番、32人のときは32番が残るのです。なんとも美しい結果ですよね。

３．一般の人数に対して攻略する。

ひとまず、2,4,8,16,32,64,…などの「2の冪乗の人数」に対しては、もはや一瞬で回答できるようになりました。では、今回最初に例で出てきた20人のように、一般の人数の場合、どう考えればいいでしょうか。
通常、「極端に簡単な例」から「一般の場合」を攻略することは非常に難しいのですが、その違いを考えることでいとも簡単に解決することができます。

20人の場合は16人の場合に比べて4人多いです。これを意識して1人ずつ座ってもらいましょう。1番、3番、5番、…と座っていきます。そして、7番が座ったところで一旦止めます。もうお気づきでしょうか。いま4人が座りました。この瞬間、立っているのは16人です。

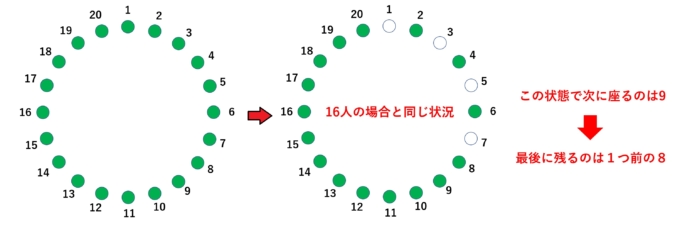
この状態を16人の場合として考えることで、次に座る9番の１つ前である8番が最後に残るのだということがわかります！鳥肌が立ちました！

これを応用すると例えば35人の場合、1番、3番、5番の3人が座った時点で残りは32=\(2^5\)人。よって次に座り始める7の一つ前である6番が最後に残ることがわかります。素晴らしい論理展開ができました！

４．さいごに

いかがでしたでしょうか。一見複雑そうに見える問題でも、まずは「愚直に試す」。そして「極端に簡単な例」を考え、うまく「違いをつかみ、一般化する」。この流れが問題解決の定石となります。なお、このような実験的・発見的に数学をとらえていくための参考書として以下の本をおすすめいたします。

実験・発見・数学体験 (数学書房選書3) 小池 正夫 (著) 数学書房

出版前、小池先生の授業でこの本の内容のいくつかを受け、当時非常に感動した覚えがあります。

和からではご自身のペースで学びたいことを学びたいだけ学ぶことができます。算数や数学の苦手意識克服、お仕事で使う計算から実務に役立つデータ分析まで、幅広く対応いたします。ご興味がある方はぜひ一度無料セミナー、無料個別カウンセリングにご相談ください。

<文/岡本健太郎>