日常生活でつかむベイズ統計
公開日
2019年8月4日
更新日
2019年8月4日

この記事の主な内容
1.人間の思考と人工知能
昨今の人工知能ブームで、「機械学習」や「ディープラーニング」といった言葉を、雑誌やテレビなどあらゆるメディア媒体で聞くようになりました。しかし、ブームではあるものの、なんだかすごく難しそうな印象がありますよね…。
しかし、人工知能のアイデアはとてもシンプルで、私たちが日常生活で行う思考がそのまま機械学習などの技術に応用されています。“人工知能”といっても、モデルになっているのはあくまで私たち人間の思考なのです。
今回は数式をほとんど使わずに機械学習の基礎となる「ベイズ統計」について簡単に解説します。
2.ショッピングでみえてくるベイズ統計の考え方
「お店で商品を効率よく探す」ときに行われる人間の思考を考えてみましょう。ここでは少しそそっかしい性格の健太くんに登場してもらいます。
健太くんは「白いTシャツ」を探しにショッピングセンターへやってきました。
健太くん「どのフロアから見ていこうかな?入口の近くにフロアガイドがあったから、これを利用してなるべく早くTシャツを買って帰ろう。」
健太くんはフロアガイドを見ました。
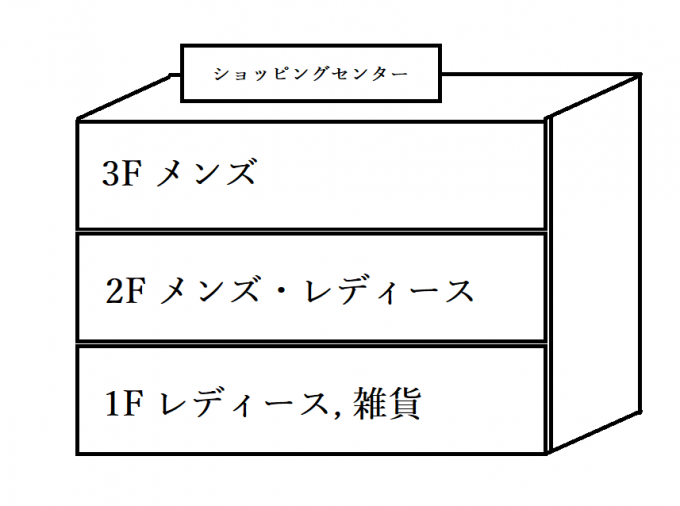
健太くん「メンズだし、3階に行けば見つかる可能性が高そうだな。」
というわけで健太くんはTシャツが見つかる確率の一番高そうな3階から攻めていくことにしました。
健太くん「3階に着いた!さっそく探そう。といっても僕、結構見落としがちなタイプだから、果たして今日中にTシャツが見つかるか正直不安だな(苦笑)。」
とにかく、健太くんは健太くんなりに一生懸命3階を探し回りました。
(10分後)
健太くん「この階はたしかにメンズ専門のコーナーだったけど、柄の入ったTシャツが多くて僕が見る限りでは3階では白い無地Tシャツは見つからなかったなぁ…。」
そう言って健太くんは次にどこを探すかフロアマップを見て考えます。
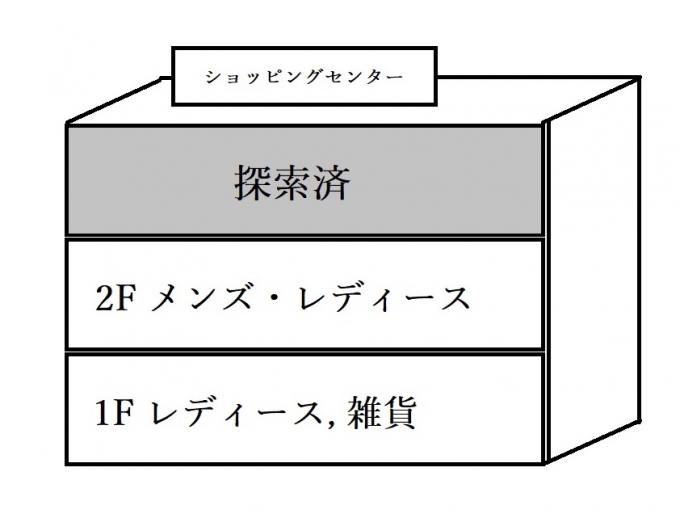
健太くん「3階を見落としている可能性もあるけど、現段階で可能性が一番高いのは2階だな。」
効率を重視して健太くんは確率の高そうな2階を選びました。
2階に着いた健太くんは早速探索を開始します。この階はレディースも多いですが、メンズは比較的シンプルな柄のものが多いようです。
(5分後)
健太くん「あ、白い無地!ようやく見つけました。白い無地のTシャツ無事購入です。」
健太くんがなるべく効率よくTシャツを探そうとしたように、私たちも普段からこうした「可能性」や「確率」を思考の中で大雑把に考えて行動を選択しています。
ベイズ統計を用いることでこうした確率を具体的に数値化し、計算できます。つまりベイズ統計とは人の思考のモデルとなっているのです。今回の健太くんの思考を数値化する準備のために、次章でベイズ統計を説明します。
3.ベイズ統計
それではベイズ統計について簡単に説明をしましょう。
状態\(A\)である確率を\(P(A)\), 状態\(B\)である確率を\(P(B)\)とします。少し抽象的なので例を挙げると、
$$P(\mbox{良い写真})\mbox{:「良い写真が撮れる確率」}$$
といった具合です。今回は簡単のために、天気、写真は「良い」か「悪い」かのいずれかであり、どちらになるかは客観的に確定しているとします。
また、「状態\(A\)の条件のもとで状態\(B\)となる確率」を\(P(B|A)\)と書きます。例えば
という感じです。同様に、
なので、結局天気に関係なく良い写真が撮れる確率\(P(\mbox{良い写真})\)は
で計算できます。さて、ベイズ統計においてカギとなるのは以下の公式です。
ちょっとイメージがつきにくいと思いますので、例を見てみましょう。
つまり、
- 「良い天気の日には\(40\%\)の確率でいい写真が撮れる」
- 「毎年この時期だと\(60\%\)の確率で良い天気になる」
- 「自分の力量だと、天候に関わらず良い写真が撮れるのは\(30\%\)ぐらいかな」
といった、「経験」や「事前の情報」でわかる確率から、
「良い写真が撮れたとき良い天気である確率」
という直接知ることが難しそうな確率を「良い写真が撮れた」という結果から求めることができるのです。
実際に公式を使って計算してみます。「経験」や「事前の情報」でわかる確率は、
となるため、「良い写真が撮れたとき良い天気である確率」は
と計算できます。
データ(結果)から特徴(原因)を推定するということは機械学習の根本となる考え方です。この簡単な例からも、実際に試してみた結果から知りたい情報(確率)をどう計算するのかがわかっていただけたと思います。
4.Tシャツ探索をベイズ統計の視点で
健太くんがTシャツを探したときの思考を、ベイズ統計を用いて数値化してみましょう。
①「確率の一番高そうな3階」という設定
各フロアに白いTシャツがおいてある確率を各階それぞれ主観的に設定してしまいます(「フロアガイド」という事前に得た情報をもとに、たぶんこんな感じだろうという具合で構いません)。
| 3階にある確率 | \(50\%\) |
| 2階にある確率 | \(45\%\) |
| 1階にある確率 | \(5\%\) |
②「結構見落としがち」という探索能力
そのフロアにTシャツがあったとしても見つけられる確率は\(70\%\)であると設定します。
※この「\(70\%\)」というのはだいたいの数値(主観的な数値)で構いません。
③「3階では見つからなかった」という結果
このとき、「見つけることはできなかったけれども、実はTシャツは3階にある確率\(P\)」というものがベイズの公式を用いることで割り出せてしまいます。この確率\(P\)は
と計算でき、3階で見つからなかったという探索結果を踏まえて、各フロアにTシャツがおいてある確率は
| 3階にある確率 | \(23\%\) |
| 2階にある確率 | \(69.3\%\) |
| 1階にある確率 | \(7.7\%\) |
と修正できます。この確率の修正をベイズ更新といいます。具体的な計算式は「天気と写真の例」とほぼ同じであるため省略します。
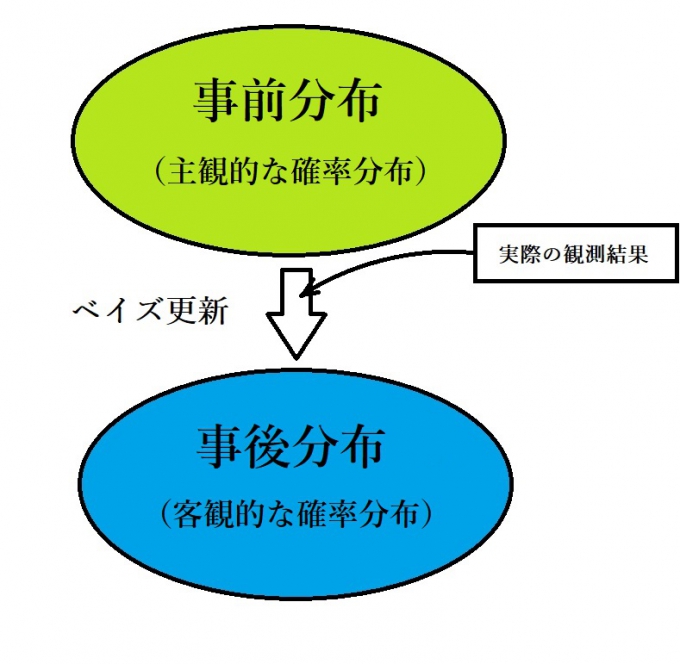
事前に設定する主観的な確率を、実際に観測した結果に応じて修正していく。これがベイズ統計を用いた今回のTシャツ探索のお話です。こうしたショッピングや探し物をする際、普段人は数値化などせず、「次はここを探そう」というように感覚的にベイズ統計を使って処理しています。
正直なところ、Tシャツを探す程度で、このような数値計算・分析を行う必要はないと思いますが、考え方自体は非常に重要です。実際にこの分析方法は、広大な海に沈んだ潜水艦やマグロの探索などにも応用されています。
5.まとめ
最近よく話題に出てくる「人工知能」や「機械学習」。そのベースとなるものは数学であり、
その中のベイズ統計の考え方は非常に幅広く応用されています。なぜこの統計の理論が扱われるのかというと、人の思考をもとにした非常に自然な考え方がベイズ統計だからなのです。
ベイズ統計に限らず、多くの数学は自然な考え方を基礎として理論が構築されています。その自然な考え方の先に、思いもよらないところで私たちは恩恵を受けているのです。
ベイズ統計に関してオススメの書籍は下記の2冊となります。
1・史上最強図解 これならわかる!ベイズ統計学 涌井良幸 涌井貞美 (著) ナツメ社
こちらはとにかく初心者にもわかりやすいと評判の書籍です。
2・しくみがわかるベイズ統計と機械学習 手塚 太郎 (著) 朝倉書店
ベイズ統計~機械学習までを視野に入れたものでややレベル高めですが、それでもわかりやすい印象です!
<文/岡本健太郎>
⇒ 講師紹介ページへ
お問い合わせページへ














