やさしく学ぶ統計学~ジニ係数とローレンツ曲線の関係~
公開日
2023年3月9日
更新日
2023年3月9日
みなさんこんにちは。和からの数学講師の伊藤です。先日のマスログでは、ローレンツ曲線を使ったデータの不均一さの表現をご紹介しました。今回は、このデータの不均一さを数値で表現する、ジニ係数と呼ばれる指標を扱います。前回の記事も参照しながらご覧いただけますと幸いです!
この記事の主な内容
1. 「不均一なデータ」とローレンツ曲線
今回は、以前の記事と同様に次の度数分布表を使います。
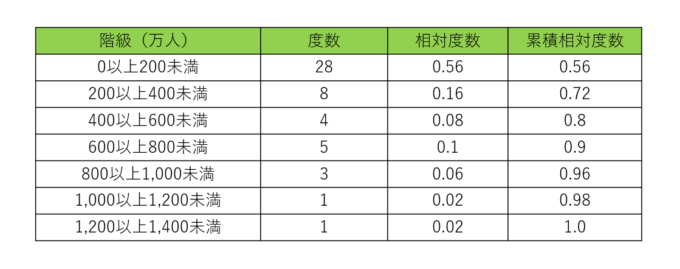
ある国における都市別の人口について、相対度数、累積相対度数を使って集計したものです。また、このデータに関するローレンツ曲線を作成する際には、この他に累積相対人口という指標を使っていました。これは階級ごとに属する都市の人口の総和をもとめ、その値の全体に対する割合を累積させたものでした。今回は以下のような関係になっています。
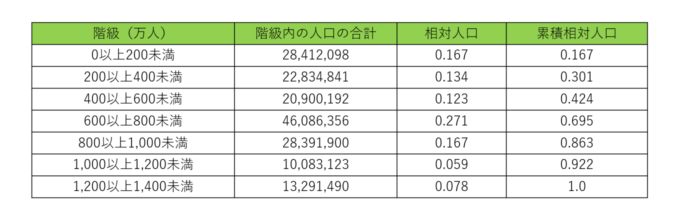
以前の記事では具体例を使ってお話をしています!
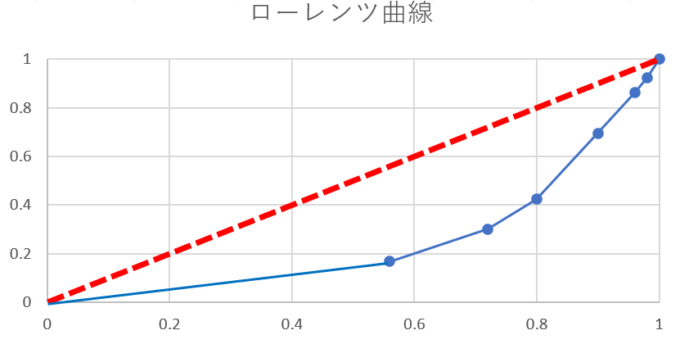
横軸に累積相対度数、縦軸に累積相対人口をとり、このデータを描いたグラフがローレンツ曲線になります。この曲線が、完全平等線(図中の赤い点線)から離れているほど、データが不均一であると見ることができました。なお、このローレンツ曲線は散布図に線を付けた形で表現しております。
次章では、このデータの不均一さを数値化するジニ係数を導入します。
2. ジニ係数とは
ローレンツ曲線と完全平等線がどれくらい離れているかを数値化するためには、2つのグラフによってできる領域の面積を使って表現します。2つの曲線に囲まれてできる領域をA、ローレンツ曲線とx軸に囲まれてできる領域をBとしましょう。このとき、領域Aと領域Bの面積の和に対する領域Aの面積の比を、ジニ係数と呼びます。
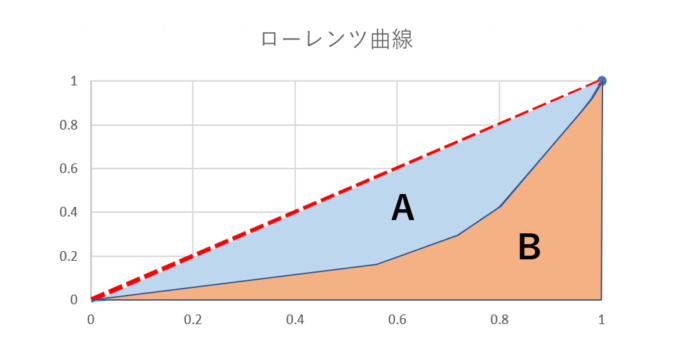
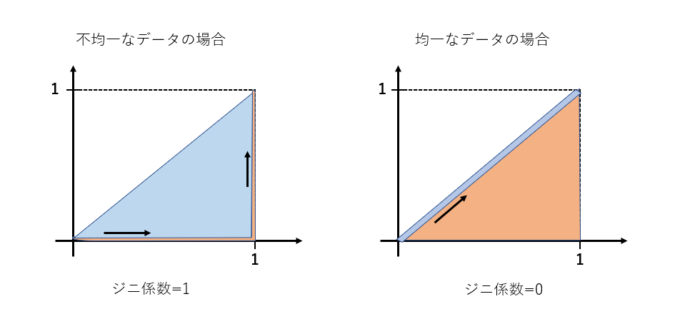
今回のデータの場合、1つの都市に国民全員が在住しており、他の都市の人口は0という状況が、データが完全に不均一と言える状況です。この場合、ローレンツ曲線はx軸を通り、点(1,0)を経由して点(1,1)に向かう折れ線となります。この場合、ジニ係数は最も大きくなり、値は1です。逆にすべての都市に同じ数の人が住んでいる状況がデータが完全に均一な状況と言えますが、この場合ローレンツ曲線は完全平等線に一致し、ジニ係数は0となります。このように、ジニ係数には0から1の値をとり、データが均等であればあるほど0に近くなるという性質があります。
なお、領域Aと領域Bを足した部分は直角二等辺三角形であり、その面積は0.5です。0.5で割り算をするのは2倍するのに等しいので、ジニ係数の計算式の見方を変えると、領域Aの面積を2倍すれば良いということが分かります。
\begin{align*}
\text{(ジニ係数)}=\frac{\text{(領域Aの面積)}}{\text{(三角形の面積(0.5))}}=2\times \text{(領域Aの面積)}
\end{align*}
したがってジニ係数を計算する際は、完全平等線とローレンツ曲線に囲まれた部分の面積を2倍するという方針がおすすめです。データの不均一さを可視化したローレンツ曲線と、その数値化をするためのジニ係数の考え方は、ぜひセットで覚えていただければと思います!
●和からのセミナー案内
Excelを用いたデータ分析のストーリーや可視化のスキルを学んでいくセミナーのご紹介です。興味を持っていただけた方は、ぜひ覗いてみてください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>













