↓↓↓動画で見たい方はこちら↓↓↓

空間図形（立体）とは

空間図形（立体）とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。
立体にはどのようなものがあったのかをまとめた記事があるので、立体について少し心配な方は以前の記事をぜひご覧ください。
（参考：空間図形（立体）の総復習（四角柱、四角錐・円柱、円錐編）【算数からやさしく解説】）

四角柱、円柱の体積の考え方

柱と錐で体積の計算方法が変わってくるので、まずは、四角柱、円柱の体積について解説していきます。
まずは前回の直方体の復習をしてみましょう。
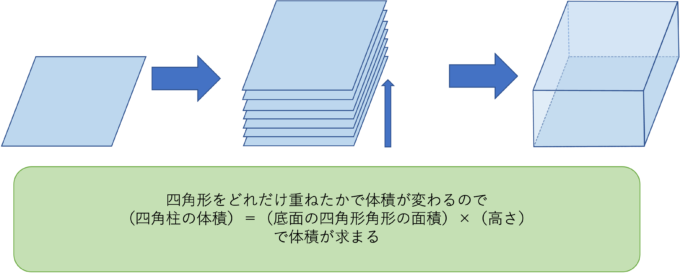
体積とは
平面の図形をどれだけ「高さ」の方向に積み重ねたか
で考えました。
四角柱の体積についても同じような考え方で体積の式を求める事ができる。底面の四角形の面積が求められれば、
（四角柱の体積）\(=\)（底面の四角形）\(×\)（高さ）
で求められる事がわかます。

直方体に関しての記事は以下をご覧ください。
（参考：空間図形（立体）の体積の求め方（直方体・立方体））
同じように円柱の体積も
（円柱）\(=\)（底面の円の面積）\(×\)（高さ）
となります。

四角錐、円錐の体積

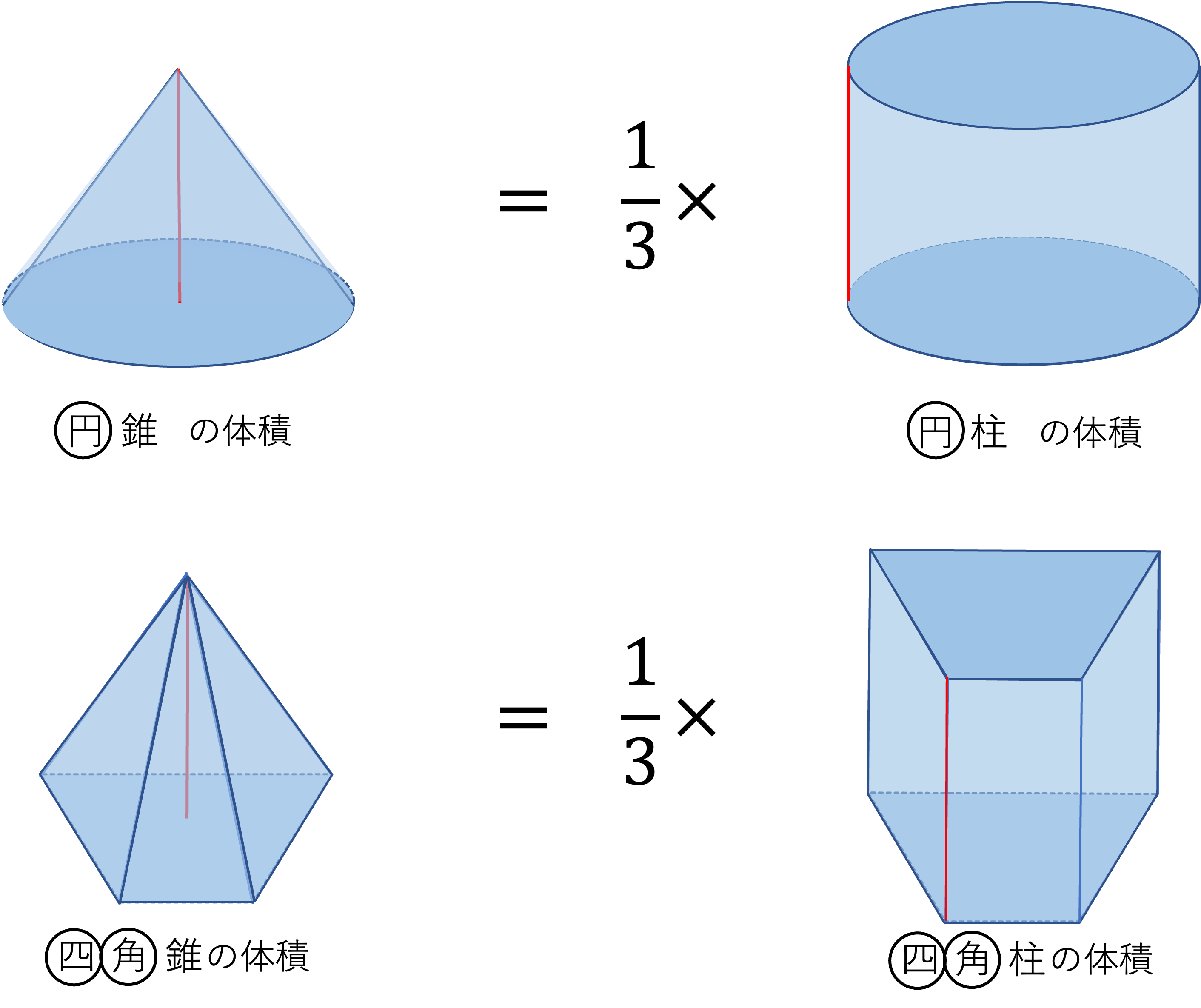
円錐や四角錐などは上が尖っているので、同じ底面円柱、四角柱の高さが同じであれば下図のようにそれぞれの体積より小さくなり、基本的に〇〇錐の体積は〇〇柱の体積の1/3になります。

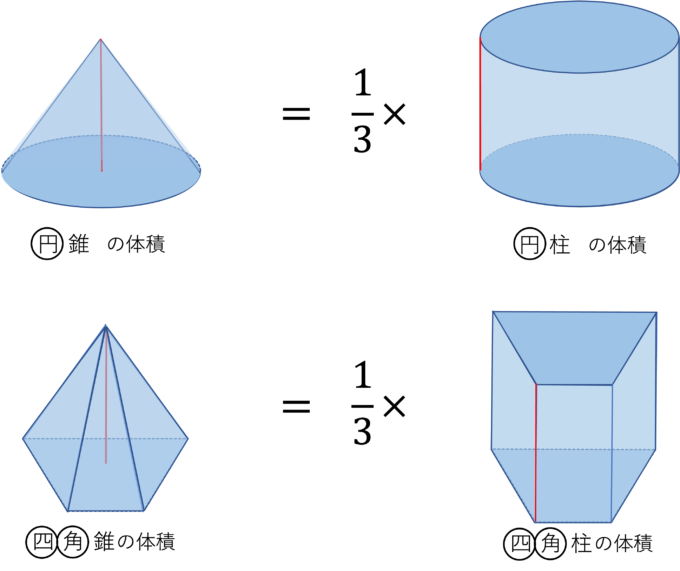
つまり、四角錐、円錐の体積はそれぞれ
（四角錐の体積）\(=\frac{1}{3}×\)（四角柱の体積）
　　　　　　　　\(=\frac{1}{3}×\)（底面の四角形の面積）\(×\)（高さ）
（円錐）\(=\frac{1}{3}×\)（円柱）
　　　　\(=\frac{1}{3}×\)（底面の円の面積）\(×\)（高さ）
となります。
なので、「錐」の形の図形の体積を求めるときは\(\frac{1}{3}\)をつけることを忘れないようにしましょう。

実際に体積を求める

それでは実際に円柱と円錐の体積を求めてみましょう。
今回はそれぞれ半径が\(2\)、高さが\(3\)の円柱、円錐としましょう。
底面の円の面積は\(2×2×\pi=4\pi\)になるので、高さが3であることからそれぞれの体積は
（円柱の体積）\(＝3×4\pi=12\pi\)
（円錐の体積）\(=\frac{1}{3}×3×4\pi=4\pi\)
となります。ここでも円「錐」の\(\frac{1}{3}\)を忘れないようにしましょう。

柱・錐の体積の活用

なぜ、\(\frac{1}{3}\)になるのかについては特別な形を除いては、厳密には高校以降で学ぶ積分というものの知識が必要になってしまいます。
また、前回に説明したように体積、面積に長さに関する数がそれぞれ\(3\)個、\(2\)個ずつ含まれています。
今回解説した体積を求める式は全てこの法則に従ってる事がわかります。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

空間図形（立体）の体積の求め方（三角柱、三角錐編）【算数からやさしく解説】

<文/尾崎>