五色定理とグラフ理論①―握手補題の証明―

算数・物理・数学トピック

公開日

2022年7月4日

更新日

2022年7月4日

こんにちは。和からの数学講師の岡本です。今回は前回に引き続き、「塗り絵」に関する問題を、数学的に取り扱うことについて簡単にまとめていこうと思います。

この記事の主な内容

１．色分けとグラフ理論

色分けを数学的に取り扱うために、グラフ理論を利用します。以前グラフ理論について簡単にまとめた記事があるので、そちらも併せてご覧ください。

塗り絵と数学～四色定理～

グラフ理論で考えるグラフ（Graph）というのは、「点（頂点）とそのつながり（辺）の情報」のことを指します。こうした点とそのつながり（辺）の情報について考察していくのがグラフ理論です。まず、与えられた平面上の塗り絵に対し、各面を点と考えます。そして、２つの面が隣り合っている場合、面に対応させた点同士を線でつなげます。こうして、塗り絵をグラフに対応させることが可能になります。例えば以下の図のような対応を考えます。

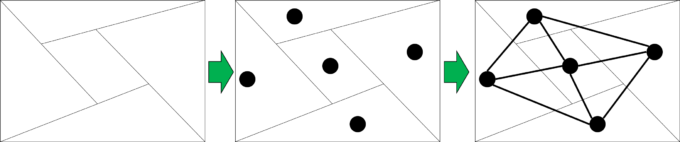
こうしてグラフ理論の視点から塗り絵の色分け問題を考察することが可能になり、実際に前回ご紹介した「四色定理」が証明されました。しかし残念なことに、証明はコンピュータを用いることによる力技な部分があり、理論（＝紙とペン）だけでの証明はいまだになされていません。そんな中で、四色ではなく、「少なくとも五色あれば十分である」という事実（以降、「五色定理」と呼ぶことにします）は、比較的簡単に証明することができます。本シリーズでは、この「五色定理」の証明を目標として解説していきたいと思います。

２．グラフ理論の言葉使い①（グラフの定義）

せっかくなので、グラフ理論で扱われる独特の言葉使いについてまとめておきましょう。まず、グラフの「点」のことを頂点（Vertex）、結んでいる線のことを辺（Edge）といい、それぞれの集合を\(V, E\)とします。簡単のため、2つの頂点\(v, w\in V\)を結ぶ辺は\(vw\)(あるいは\(wv\)）と表すことにします。そうすることで、\(V, E\)の２つの集合の情報さえあればつながりの情報は再現できます。そのためグラフ\(G\)は\(G=(V,E)\)という、集合のペアで表現します。

例えば、\(V=\{v_1, v_2, v_3, v_4\}, E=\{v_1v_2, v_2v_3, v_3v_1, v_1v_4\}\)とすれば、グラフ\(G=(V, E)\)は以下のようなつながりであることがわかります。

３．グラフ理論の言葉使い②（グラフの特徴）

グラフには様々な種類がありますが、今回扱っていくグラフは「シンプル」なものとします。例えば、頂点から同じ頂点に伸びている辺のことをループ（loop）、2つの頂点に2本以上の辺が伸びていることを多重辺（Multiple edge）といいますが、今回はこういった特徴を持つグラフは扱いません。このように、ループや多重辺を持たないグラフのことを単純グラフ（Simple graph）といいます。

また、1つの頂点に接している辺の個数をその頂点の次数（degree）といい、頂点\(v\in V\)の次数を\(\deg(v)\)と表現します。比較的簡単に示されるグラフ理論の興味深い命題として次の「握手補題（Shake hands lemma）」というものがあります。

(握手補題)
単純グラフ\(G=(V,E)\)に対して、以下が成り立つ。
\begin{align*}
\sum_{v\in V}\deg(v)=2|E|
\end{align*}

つまり、どんな単純グラフに対しても、各頂点の次数を合計すると辺の数の2倍と等しくなるという、面白い命題です。一見すると本当に成り立つのか疑わしいので、具体的なグラフに対して考えてみましょう。例えば以下のような単純グラフ\(G=(V,E)\)について、辺の数を数えてみましょう。

辺の本数は8です。では続いて各頂点の次数を求めてみましょう。

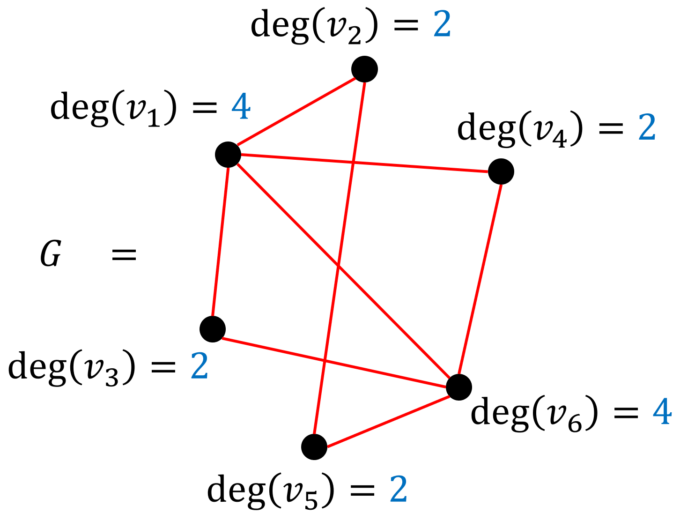
上の図のように各次数がわかれば、これらを全て合計してみましょう。

\begin{align*}
\sum_{v\in V}\deg(v)=4+2+2+2+2+4=16.
\end{align*}

よって、次数の総和は16となり、たしかに辺の本数の2倍と一致します！このように非常に面白い命題ですが、証明は意外とシンプルです。先ほどのグラフに対して次の図のように、グラフの各頂点周りの辺に丸い点（黄色）を置きます。つまり、頂点の次数の総和はこの丸の数ということになります。

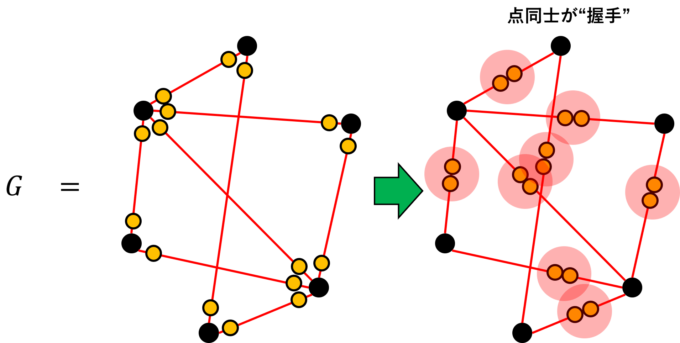
そしてこの点を辺の中央に向けて移動させると、各辺の上で黄色い点が2つ並ぶように整理できます。これは点同士が“握手”しているように見えるので、この命題は「握手補題」といわれています。さて、このように、全ての辺の上に2個ずつ黄色い点が配置されているので、黄色い点の総和は、単純に「２×辺の数」と考えることができ、握手補題が証明されました。