視聴率調査はどれくらい正確?
公開日
2022年7月7日
更新日
2022年7月7日

動画で見たい方はこちら↓↓↓
みなさんこんにちは。和からの数学講師の伊藤です。突然ですが、朝の情報番組でこんなやり取りを目にしたことがある方も多いかもしれません。
「今期のドラマの見どころはこの二つです!
関東地方の視聴率を見てみるとこの通り、Aドラマは10.0%、Bドラマは9.2%!
Aドラマに軍配が上がる結果となりました!
やはり豪華な配役に惹かれる視聴者が多いのでしょうか!」
視聴率と言えば、その番組をどれくらいの割合の人たちが見ていたか調べるものです。
視聴率が高い番組は人気の証。だからこそ、テレビ局の方々はこの数字を何よりも重要視しています。今回は統計学の視点から、視聴率ってどれくらい正確なの?というお話をしていきたいと思います。
この記事の主な内容
1.そもそも視聴率ってどうやって計っているの?
さて、皆さんは視聴率調査に参加されたことはありますか?
「テレビを見ているのだから、毎日どの番組を見ていたか調べられているのでは?」と思われる方も多いかもしれません。しかし、視聴率調査というのは全数調査ではなく、標本調査です。つまり、一部の世帯(もしくは個人)に協力をお願いして、その方々の番組視聴データから、それぞれの番組を見ていた世帯の割合を計算しているのです。
では、我々が普段目にする視聴率調査では何世帯が調査対象となっているのでしょうか。これは地域によっても違うのですが、関東地方では2700世帯が調査対象となっているようで、中には200世帯の調査で視聴率を計算している地域もあるそうです。意外に少ないと思いませんか?しかし、おそらくこれは「十分に正確」な視聴率をはじき出すために設計された数字なのです。標本数がどうして重要になるのか、次の章で見ていきましょう。
2.標本数はなぜ重要?
先ほどお話した通り、視聴率を調べるためにはランダムに選んだ数百~数千世帯の番組視聴データを観測し、割合を算出します。関東地方での視聴率を報道する際に、実際に関東全体でその番組が見られていた割合である「真の視聴率」を計測するのは現実的ではないので、一部の世帯の視聴率を調査して真の視聴率を推定したものが、普段我々が目にしている視聴率ということになります。つまり、真の視聴率は11.5%だったのだけれど、標本から推定した結果「Aドラマの視聴率は11.2%でした!」と報道されることになるわけです。
では、視聴率調査には何世帯に協力してもらえばいいのでしょうか。標本となる世帯が多ければ多いほど、調査は正確なものになります。「誤差を考慮すると、真の視聴率は3%から43%の間ぐらいです!」なんて幅広い値で言われても意味がありませんので、この幅はなるべく狭くしたいものです。そして標本数を増やすことによって、この幅を狭くすることができるのです。とはいっても100万世帯に協力をお願いするとなるとコストがかかりすぎるため、ちょうどよい標本数を決める必要が出てきます。
さて、先ほど関東地方の視聴率調査は2700世帯で行っていると書きました。この2700というのが、ある程度の正確さを保証するための値であると思われます。では、2700世帯への調査でどれくらい正確な推定ができるのか、これも統計学を使って解明することができます。
3.信頼区間
適切な標本数について考えるために、統計学でよく使われる「信頼区間」という言葉をご紹介します。信頼区間は、「真の視聴率はだいたいここからここの間!」と言うときの区間にあたります。信頼区間というのは2700世帯を調べた時点で計算される値なので、また別の2700世帯で信頼区間を計算すると違う区間になります。統計学では○○%の信頼区間という言い方をするのですが、95%の信頼区間と言ったら、次のようなことを表しています。
2700世帯を調査して95%の信頼区間を計算する作業をたくさん行うとする。そうして作った区間のうち95%は、真の視聴率の値を含む。
「95%の確率で真の視聴率が区間に含まれる」幅を95%信頼区間と呼ぶと少し語弊があるのですが、わかりにくければ一旦そのような解釈をしていただいても大丈夫です。
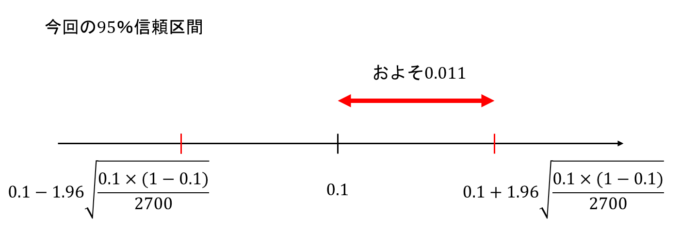
さて、2700世帯を調査して視聴率が計算されるわけですが、その結果が0.1、つまり10%だったとします。このとき、この調査の95%信頼区間を考えてみましょう。信頼区間は以下のような式で計算することができます。
\begin{align*}
\left[ 0.1-1.96 \sqrt{\frac{0.1 \times (1-0.1)}{2700}}, 0.1+1.96 \sqrt{\frac{0.1 \times (1-0.1)}{2700}} \right]
\end{align*}
(※\([a,b]\)というのは、両端を含めた\(a\)から\(b\)の区間という意味です。)
この区間の右端を電卓で計算してみると、約0.11になります。このことから、信頼区間は\([0.089, 0.111]\)と、2%くらいの幅を持っていることがわかりました。
4.視聴率はどれくらい正確なの?
前章の内容を踏まえて、視聴率調査はどれくらい正確なの?という疑問に答えてみましょう。10%前後の視聴率の番組を2700世帯の標本で計算すると、信頼区間の幅が2%程度になることがわかりました。
ということは、この視聴率調査では、±1%ぐらいの誤差は生まれてもおかしくないということになります。この視点で、この記事の初めに書いたニュースをもう一度見てみましょう。
「今期のドラマの見どころはこの二つです!
関東地方の視聴率を見てみるとこの通り、Aドラマは10.0%、Bドラマは9.2%!
Aドラマに軍配が上がる結果となりました!
やはり豪華な配役に惹かれる視聴者が多いのでしょうか!」
Aドラマの視聴率の信頼区間は±1.1%の幅を持っていて、Bドラマの方も±1%くらいの幅を持っています。ということは、実はこの調査では、Aドラマのほうが視聴率が高かったと言い切ることはできないのです。つまり、誤差の影響でたまたまAドラマが良い視聴率だっただけで、真の視聴率はBドラマの方が高かった可能性も十分に考えられる結果だったということです。
5.まとめ
いかがでしたでしょうか。テレビ番組で報道された視聴率が、必ずしも正しいとは限らない…というお話をしてきました。「僅差で視聴率トップ!」と言われていた番組も、もう一度調査をしたら実は2位だった、ということも十分あり得るのです。
なお、関東地方の視聴率調査は2700世帯ということで計算してきましたが、数年前までは900世帯で調査をしていたようです。先ほどの信頼区間の式を900世帯の標本で計算してみると、信頼区間には中心から±2%ほどの幅が生まれることになるため、今よりも精度が低い調査だったということになります。今後も視聴率調査が変わって、より正確な視聴率が報道されることになるかもしれませんね。
本日、信頼区間の構築などの詳細は割愛してきましたが、和からではこういったお話を、数式をほとんど使わずにマスターするセミナーをご用意しております。今回興味を持っていただけましたら、ぜひ和からのセミナーをチェックしてみてください!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/伊藤智也>













