↓↓↓動画で見たい方はこちら↓↓↓

多角形の面積

面積とはざっくりと言うと、（主に平らな）図形の大きさ（広さ）を表す量のことです。
多角形には三角形や四角形はもちろん、五角形、六角形、\(\cdots\)のようにいくつもありますが、今回は特に正多角形（すべての辺と内角がそれぞれ等しい多角形）に注目してその面積を求める方法について考えてみたいと思います。
ですが、小・中学校までで学ぶ内容では具体的に様々な正多角形の面積を求める式を作ることが難しいので、今回は考え方に注目して解説していきたいと思います。
面積についての記事や三角形、四角形、円の面積についての記事はこちらをご覧ください。

参考：面積とは【算数からやさしく解説】
参考：円の面積の求め方【算数からやさしく解説】
参考：四角形の面積の求め方【算数からやさしく解説】
参考：三角形の面積の求め方【算数からやさしく解説】

長方形の面積

少し復習ですが、面積について考えるときは初めに、面積の基準として縦・横の長さがそれぞれ1の正方形の面積を1としました。
そこから長方形の面積を求める式
長方形の面積=（縦の長さ）×（横の長さ）
が導けました。
これまでにこの式から三角形や四角形などの面積を求めてきました。

考え方

正多角形の面積を考えるときの基本的な考え方は三角形に分割することです。
正三角形についてそれ以上分割することができないので今回は省きたいと思います。

では正四角形（正方形）を他の正多角形の面積も求めるときにも使える方法を考えていきましょう。
まず、正方形には下図のように外接円（がいせつえん）（正方形の頂点をすべて通るような円）を描くことができます。
次に正方形の各頂点と円の中心とを結びます。すると小さな三角形が4個できます。これらの三角形はすべて合同（ごうどう）（まったく同じ形の図形）です。（合同の条件を知っている方は確かめてみてください）
なので、小さな三角形の面積を求めて４倍すればこの正方形の面積を求めることができるとわかります。

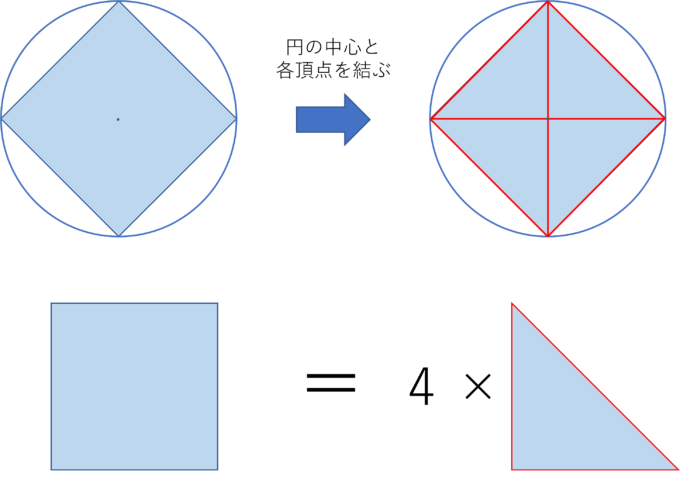
今までのことを正方形ではなく正多角形で同じように考えることができます。今は正方形で考えているので少し遠回りをして面積を求めているように感じますが、正多角形の面積を求める問題を1つの三角形の面積を求める問題に置き換えられていることは、ものの考え方として重要なことです。

本来ならここからそれぞれの正多角形に対して小さな三角形の面積を求める必要があるのですが、この式は最初にも説明したように高校以降の内容が必要になるので割愛します。

正六角形の面積

これまでで面積を求めるときの考え方について話したので、実際に1辺の長さが1の正六角形の面積を求めてみましょう。先ほどの流れの通りに進めていきます。

まず初めに、正六角形の外接円をかき、正六角形の各頂点と円の中心を結びます。

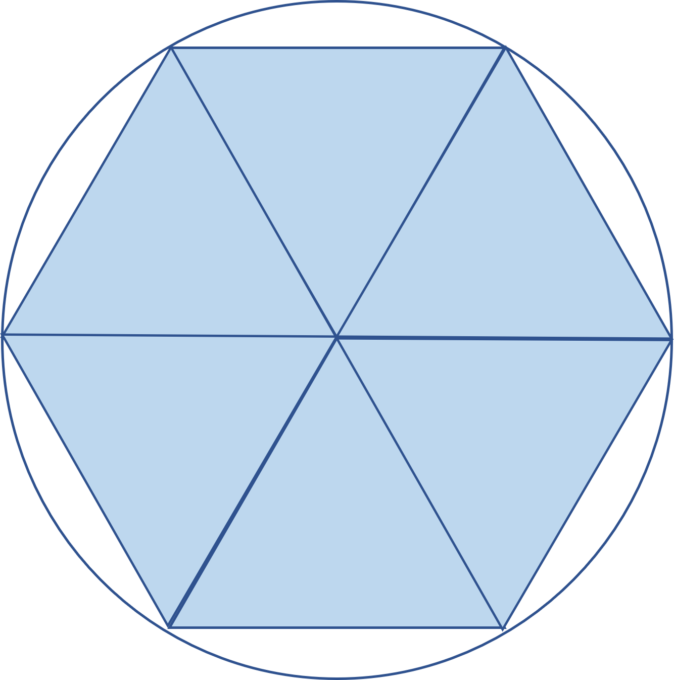
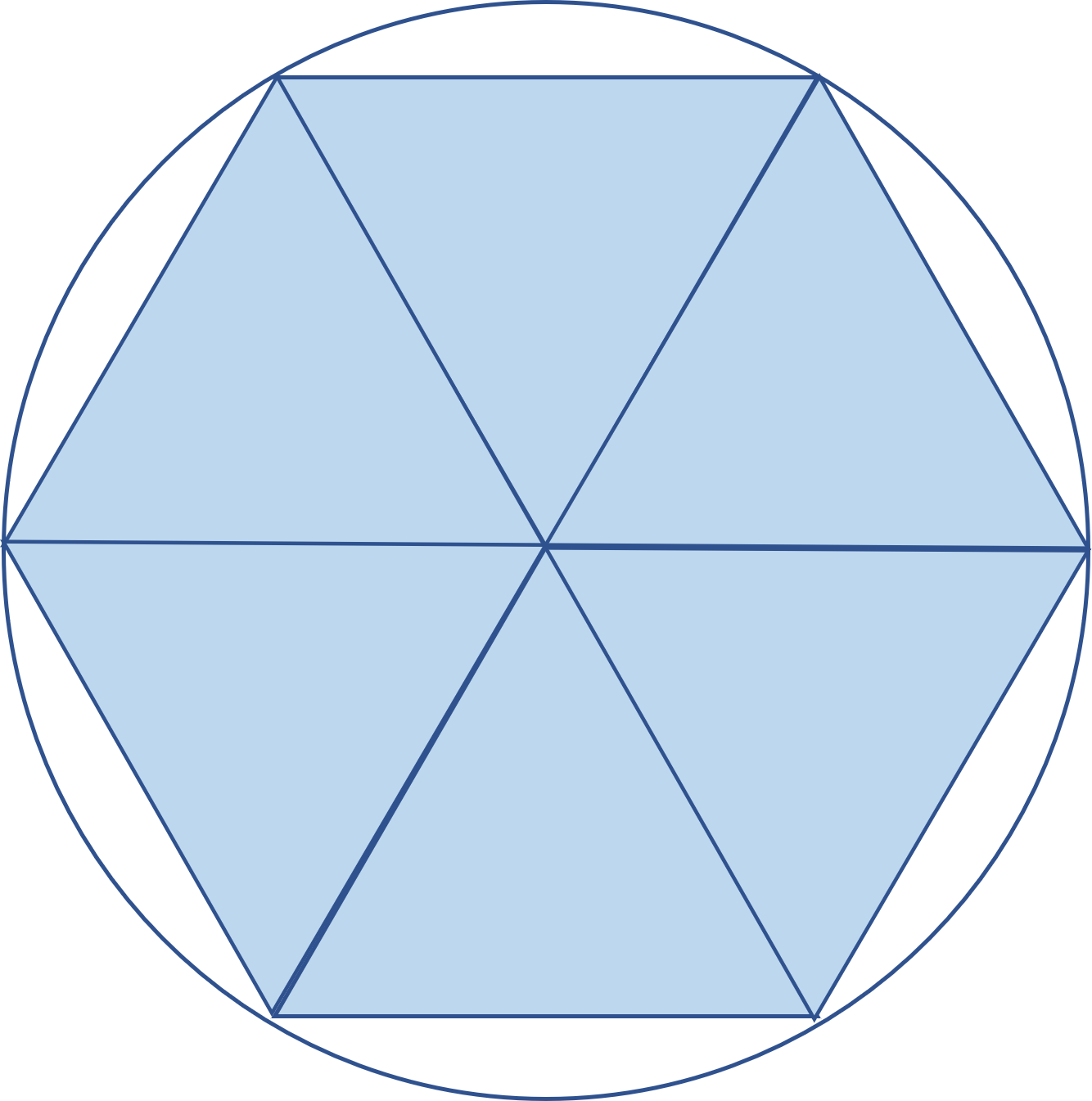
そうすると小さい合同な三角形が全部で6個できているのがわかります。
ここでこの三角形をよく見てみると正三角形であることがわかります。
（中心角と円の中心から頂点までの長さが等しいことを使うとわかります）
つまり、1辺が1の正三角形の面積を6倍すれば1辺の長さが1の正六角形の面積が求まるということです。

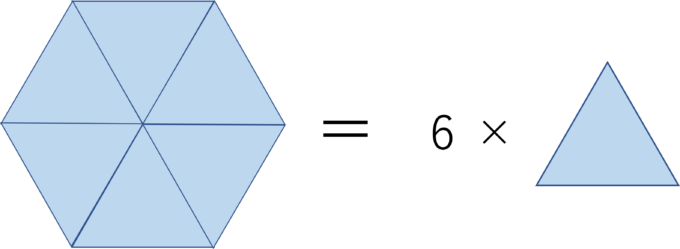
1辺が1の正三角形の面積は\(\frac{\sqrt{3}}{4}\)なので、正六角形の面積は\(\frac{\sqrt{3}}{4}×6=\frac{3}{2}×\sqrt{3}\)となります。

多角形の面積の求め方の活用例

多角形の面積をそのままの形で求めようとすると難しいですが、今回の三角形などのより簡単なものを使って分割して考えることで問題を解決することは数学ではもちろんのこと生活の中でも活用できます。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

三角形の面積の求め方【算数からやさしく解説】

<文/尾崎>