四角形の面積の求め方【算数からやさしく解説】
公開日
2022年5月1日
更新日
2025年9月18日

↓↓↓動画で見たい方はこちら↓↓↓
この記事の主な内容
四角形の面積
面積とはざっくりと言うと、(主に平らな)図形の大きさ(広さ)を表す量のことです。
四角形と言えば、平行四辺形や台形、ひし形などがあり、これらの面積の公式を覚えている方も多いと思います。
今回はこれらの面積を求める式を以下の記事で求めた長方形の面積の式を使って解説していきたいと思います。
(参考:面積とは【算数からやさしく解説】)
長方形の面積
少し復習ですが、面積について考えるときは初めに、面積の基準として縦・横の長さがそれぞれ1の正方形の面積を1としました。
そこから長方形の面積を求める式
長方形の面積=(縦の長さ)×(横の長さ)
が導けました。
長方形の面積がわかったので、ここからは図形を切ったりくっつけたりして形を変えて長方形にしたりすることで、他の図形の面積を求めていきたいと思います。
平行四辺形・台形の面積
平行四辺形は下図のように変形させることで長方形の形にすることができ、面積を求めることができます。
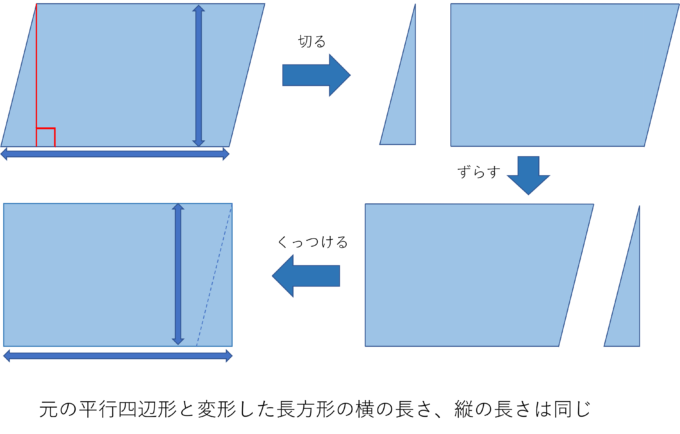
長方形の面積の求め方はわかっているので平行四辺形の面積も求められることがわかります。つまり、平行四辺形の面積を求める式は
平行四辺形の面積=(横の長さ)×(高さ)
となるとわかります。
平行四辺形の面積が求められるようになると台形の面積も求めることができるようになります。台形の面積も平行四辺形のときのように面積の求め方を知っている図形の形に変えて面積を求める公式を作りたいのですが、ここで少しトリッキーなことをします。台形をもう一つ用意します。それをひっくり返してもとの台形にくっつけます。
ひっくり返しても台形の面積は変わらないのでくっつけることでできた図形の面積は元の台形の面積のちょうど2倍になっています。どうしてこのようなことをしたのかというと、実はこうしてできた図形が平行四辺形になっているのでこの図形の面積を求めることができるのです。
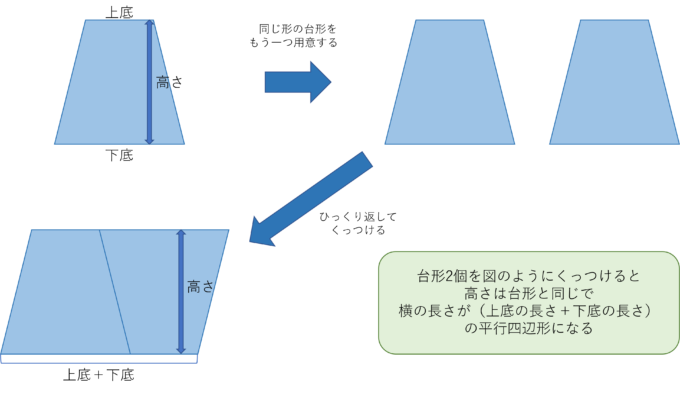
この平行四辺形の面積は(横(上底+下底))×(高さ)ですが、この平四辺形は元の台形の面積の2倍だったので半分にすれば台形の面積を求める式は
台形の面積=\(\frac{1}{2}×\){(上底+下底)×(高さ)}
だとわかります。
ひし形の面積
ひし形とは四角形の4つの辺の長さが等しいような四角形のことでしたが、そんなひし形の面積を求めてみましょう。求める方法は、これまでと同じようにひし形にいくつか手を加えて長方形にすることでひし形の面積を求めます。
どのような手を加えればいいかというと、「台形のときのようにもう一つひし形を用意して、平行四辺形のときのように切ってくっつける」です。
下図のようにするとひし形を長方形の形にすることができ、面積を求めることができます。
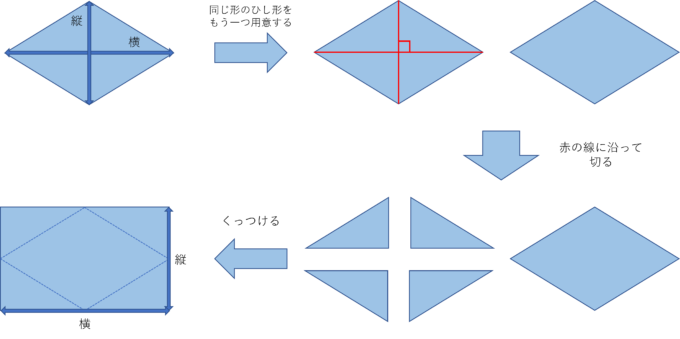
このことから、ひし形の面積はできた長方形の面積を2で割ればよいので
ひし形の面積=\(\frac{1}{2}\)×(横の長さ)×(縦の長さ)
になるとわかります。
四角形の面積の活用例
数学では基本的に縦・横(・高さ)がそれぞれ直角になっている平面(空間)を考えます。
そこで、今回のように角が直角である長方形(直方体)を使って四角形以外の様々な図形の面積を求めることができます。このようなことは1800年代の歴史的には比較的新しい理論なので大学などで学びます。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/尾崎>















