↓↓↓動画で見たい方はこちら↓↓↓

円の面積

面積とはざっくりと言うと、（主に平らな）図形の大きさ（広さ）を表す量のことです。
円と言えば、通常の円や楕円（だえん）などがあり、特に円の面積の公式は覚えている方も多いのではないでしょうか。
では、今回は実際に円の面積はどのように考えることができるのかについて、以下の記事で説明した長方形の面積を求める式を用いて解説していきたいと思います。
前回の記事をご覧になってない方はぜひこちらをご覧ください。（参考：面積とは【算数からやさしく解説】）

長方形の面積

少し復習ですが、面積について考えるときは初めに、面積の基準として縦・横の長さがそれぞれ1の正方形の面積を1としました。
そこから長方形の面積を求める式
長方形の面積=（縦の長さ）×（横の長さ）
が導けました。
長方形の面積がわかったので、ここからは図形を切ったりくっつけたりして形を変えて長方形にしたりすることで、他の図形の面積を求めていきたいと思います。

円の面積

円の面積を求めるときも他の図形と同じように、円をもうすでに面積の求め方を知っている長方形の形にすることで面積を求める式を考えてみましょう。

まず初めに円を4等分になるように切って並び替えてくっつけてみます。
次に円を8等分になるように切って並び替えてくっつけてみます。

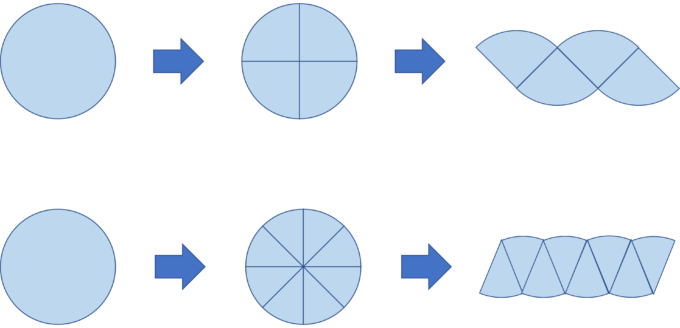
4等分にしたときよりも8等分にした時の方がより長方形の形に近いですよね。

では、この調子でどんどん円を細かく切っていくとどうなるでしょう。
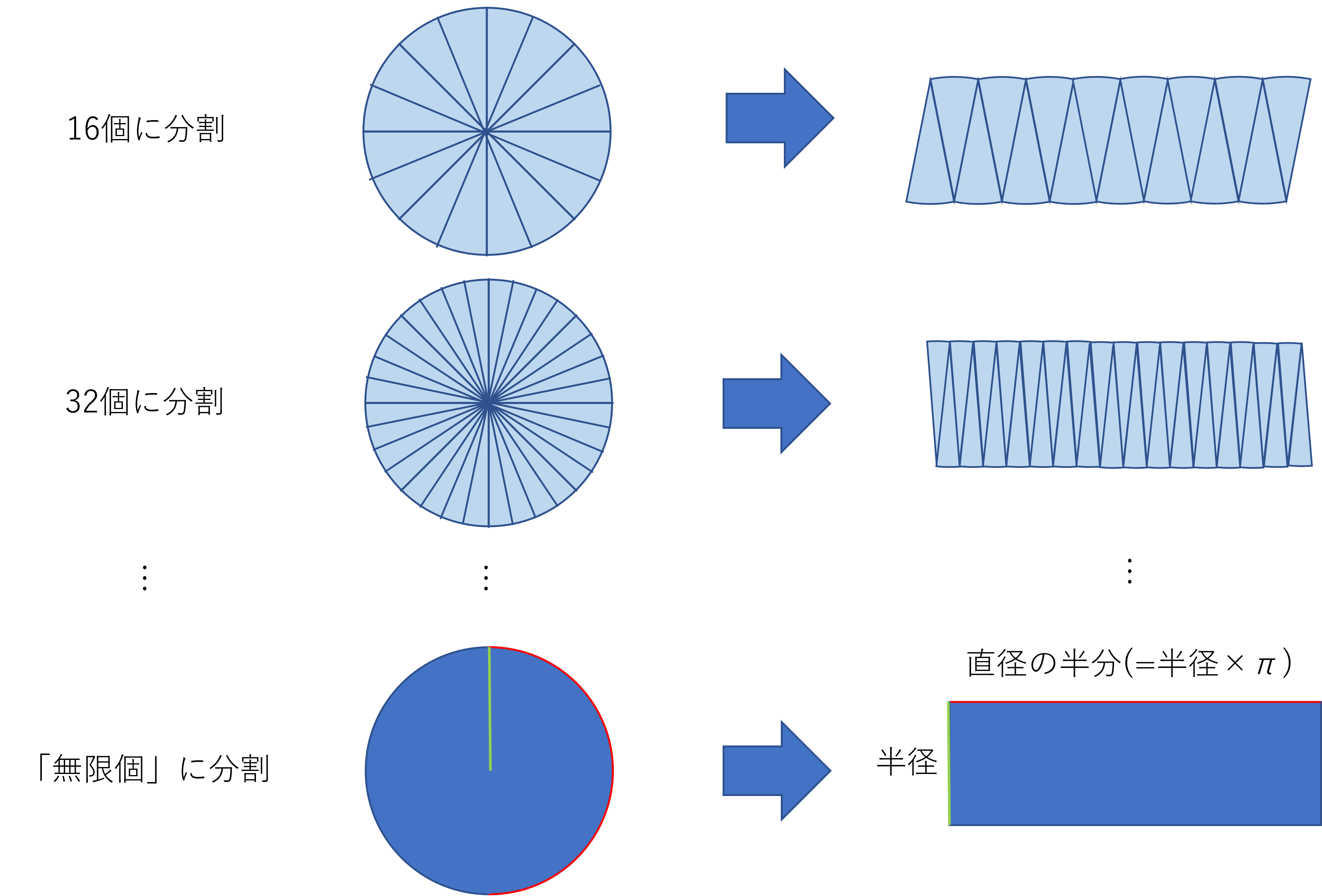
どんどんどんどん長方形に近づいていき「無限」に細かくすると長方形になります。
この長方形の縦と横の長さを考えると、縦の長さは円の半径だとわかります。
一方、長方形の上下の横の辺の長さを足すと円周の長さになるので、長方形の横の長さは円周の長さの半分だとわかります。

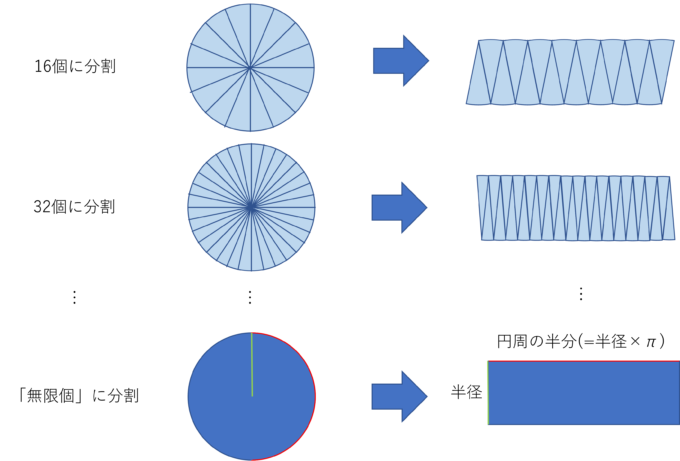
これで長方形の縦と横の長さがわかったので、円周の長さは2×半径×\(\pi\)だったことを思い出すと円の面積を求める式は
\begin{align*}
円の面積 &=(円周の半分)×(半径)\\
&=(\frac{1}{2}×2×(半径)×\pi)×(半径)\\
&=(半径)^2×\pi
\end{align*}
になります。

「無限」という単語が出てきて戸惑っている方もいるかもしれませんが、円周率\(\pi\)や\(\sqrt{2}\)などの無理数（むりすう）と呼ばれる数に関することを扱う時は基本的に「無限」に関する話が出てきてしまうので、今はそういう風に考えられるということを知ってもらえるといいと思います。

色々な図形の面積

これまで扱ってきた図形以外の図形を求めるにはどうすればいいでしょうか。
1番の基本は面積を変えずに、もしくは同じ形の図形を使って自分の知っている図形（三角形など）に形を変える考え方です。
小学校や中学校の問題で出てくるのは多角形などが多いので基本はこの考え方をもとに問題を解くことできます。
ですが、高校や大学以降では楕円（だえん）や二次関数（にじかんすう）のような、より複雑な形の図形の面積を求めることになります。

面積の活用例

高校や大学では主に積分と呼ばれる、円の面積でも出てきた「無限」をうまく使うことで曲線を含む図形の面積なども求めることができる方法を学びます。
そんな積分ですが、大学などでは面積を求めることだのみに使われることは少なく、数学はもちろん、工学や経済など私たちの生活に関することにも広く応用されています。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

四角形の面積の求め方【算数からやさしく解説】

<文/尾崎>