1カ月ほど前、講師の岡本がミーティングで突然「円周率コアラって知ってます？？？」と口火を切ります。みんな「円周率コアラ？？？」と訳が分からず。すると、コアラのマーチのパッケージを出し、「これ！！」とみんなに見せました。

なんと、こんなものがあるのか！！！資本金が円周率の弊社としては、実物を何が何でも拝みたいと思いました。

↓↓↓動画で見たい方はこちら↓↓↓

1.確率を考える

すでに岡本が数箱食べながら確認したものの、出ていなかったとのこと。
私も聞いてから、いつもより気にしてコアラのマーチを購入し、1カ月の間に7箱くらい食べました・・・が、出ないんです・・・。
そうなってくると私の検証魂に火が付きます！かつて、ディズニーツムツムで検証した時のように、何が何でも確認したくなりました。

ツムツムでガチャの確率を検証してみた

最初にネットでコアラのマーチに入っている、絵柄種類を調査し、そこから分かったのは、
・どうやら365種類あるらしい（過去からの総数だと600種類以上とのことです。）
・さらに1つ購入して中に入っている数を確認したところ、23個。
・同じ絵柄は入っていない様子。
・コアラの絵柄はすべて同じ数ずつ製造しているらしい。

つまり、1箱23個÷全種類365個＝0.063（6.3％）であるため、ある特定の絵柄が1つの箱に入っている確率は6.3%ということになります。
※簡単に考えて計算しています。

以下、今回とは関係ありませんが、調べていた時のプチ情報です。
・年に1度、10個ずつ入れ替えているらしい？
・円周率コアラは35周年企画のデザイン一般公募で追加されたものらしい。
・男の子はマーチくん、女の子はワルツちゃんというらしい。

マーチくんは知らなかった。だから、コアラのマーチなのか(笑)
本題に戻りますが、1箱6.3％で円周率コアラも出ると考えられるため、
・100÷6.3=15.8
つまり、16箱買えば、円周率コアラが1つは出ると考えました。

2.コアラのマーチを大人買いしてみる

早速、ドン・キホーテに買いに行ってみました。考えて、16箱ちょうどで確率が偏って出なかったら困るので、キリよく30箱と定めます。

これはなかなか壮観です。
きっと、ドン・キホーテのレジ店員の方は、私がどんだけコアラのマーチが好きなんだ！！！と思ったんだろうなぁ。
ただ、確認するのも大変そうで急いで箱を開けて並べてみました。
（※コアラのマーチを並べている画像は拡大できます）

円周率コアラ・・・見つからず。

次もあけて並べると・・・。

見つからず・・・。

まぁ、16箱あけないと出ないから仕方ないかぁ～と次を開けると・・・

出ない・・・。

次は・・・

もしかして、ないのかなぁ～。

次は・・・

ん？んん？？んんん？？？
おっ！あった！！あったぞ！！！本当にあったんだ。。。

5箱目で円周率コアラをついに発見です！！
円周率コアラを探してから前に7箱食べたことを考えると、今回の5箱と足したら12箱かぁ。でも、16箱よりは少ないと思い、ほっと一安心しました。

ただ、こうなると残っているコアラのマーチ山がもう不要ですが、一応調べておくことにしました。

3.30箱開けた結果、円周率コアラは何匹いたのか

ちなみに365種類の絵柄は「LOTTE」さんのサイトで確認できます。
→コアラの全種類はこちら

残り25箱開けた結果は下記のとおりです。

正確な確率の計算
講師の松中です。記事の冒頭である特定の絵柄が入っている確率は6.3%と計算しましたが、これは同じ箱には同じ絵柄が入らないという仮説の下での計算でした。検証の結果同じ箱に同じ絵柄が入り得ることがわかったため、正確な確率を計算し直します。
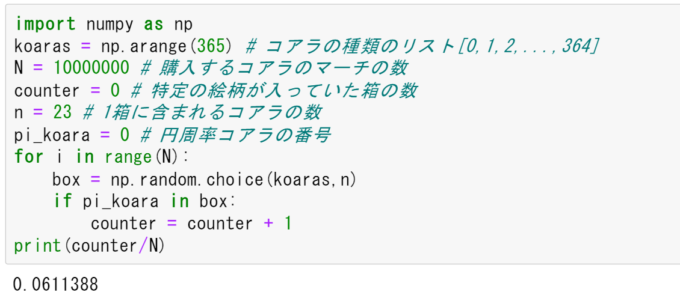
「箱の中にある特定の絵柄が少なくとも1個入る」という事象は「箱の中にある特定の絵柄が1個も入らない」という事象の余事象となっています。この余事象の確率は\(\left(\frac{364}{365}\right)^{23}\)となり、最終的に求めたい確率は\(1-\left(\frac{364}{365}\right)^{23}\)=約6.11%となります。
実際にコンピュータ(Python)で1000万箱買ってみると、特定の絵柄が入った割合は6.11%となりました。

↓↓↓以前にディズニーツムツムのガチャでプログラム検証した内容はこちら↓↓↓

楽しい確率シミュレーション

4.おわりに

さて、また、心に変な炎がともってしまい、円周率コアラを探してしまいました。「知りたい欲求」は満たせて満足だったのですが、大惨事だったのはこの後。

コアラのマーチ大発生です(笑)
タッパーで密閉できる容器に入れて、これから数日間かけて美味しくいただきたいと思います。
しかし、レアなコアラは存在せず、同じ確率だったのは知らなかったなぁ～。
円周率コアラを探していましたが、やたら気になる絵柄は「ちんあなご」がありました。

もはや、原型がコアラではないような・・・(笑)
今回はコアラのマーチで確率を考えてみました。

・統計の歴史的必要性や確率に興味がある方は、下記セミナーがおススメです。

はじめての統計検定講座～統計と教育の歴史から～

・仕事でつかえる簡単な統計を学ぶなら

ビジネス統計超入門-すぐに使える仕事力-

<文/綱島佑介>

コアラのマーチ<チョコ> 50g×10箱

コアラのマーチ クッション 31cm