鏡を使って数学的ファッションチェック!その2
公開日
2021年6月6日
更新日
2021年6月6日

こんにちは。和からの数学講師の岡本です。前回に引き続き、鏡の見方に関する話題です。前回のおさらいから入っていきましょう。
この記事の主な内容
1.直交型の鏡と斜め型の鏡
図のように、床に直交するタイプの鏡の場合、どうしても顔の方が足元よりも近くに見え、遠近感により顔が大きく見えます。対して、斜め型の鏡は、顔が遠くに映ることがあり、実際よりもやや小顔に見えてしまいます。
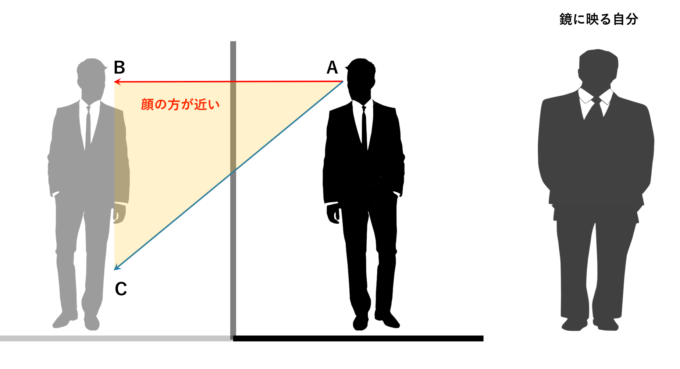
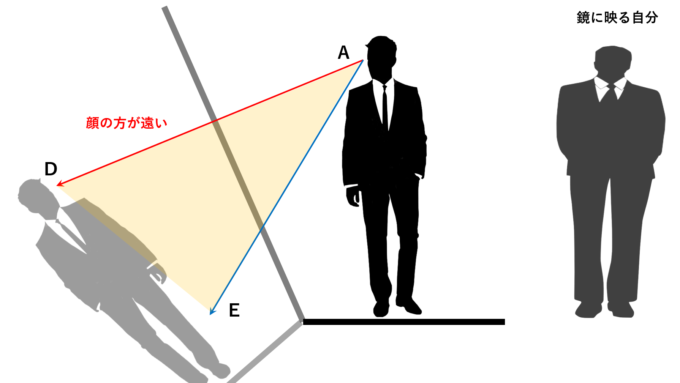
遠近感は距離の比が関係しているので、鏡からなるべく離れることで距離の差をなくし、遠近感を強調させない方法が考えられます。これは遠いほど距離の差がなくなりますが、その分細かい部分が確認できなくなってしまいます。なるべく近くで、遠近感も起こさずにファッションチェックしたいですよね。そこで数学の登場です!
2.数学を使う!
直交型の場合、どう頑張っても、顔までの距離の方が近くなります。そこで、鏡の角度をうまく調整し、顔までの距離と足元までの距離が同じであるようにすれば、全体をバランスよく見通せます(ややお腹が近くなります)。
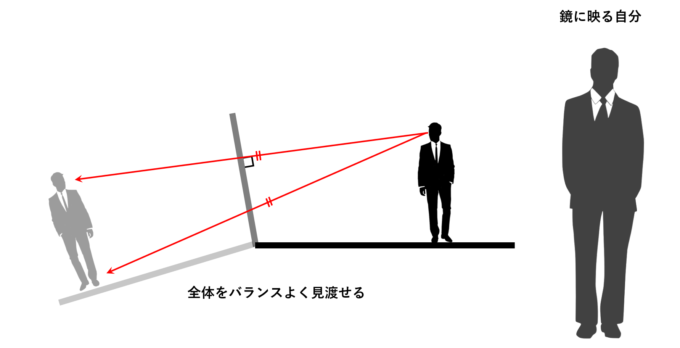
ではこの条件を求めるために簡単に次のような設定を考えることにします。
(1)鏡とXさんまでの距離を\(x\)とする。
(2)床からXさんの目までの高さを\(y\)とする。
(3)鏡の角度を\(90^{\circ}+\theta\)とする(もともと\(90^{\circ}\)であり、そこから\(\theta\)傾けた)。
このとき、以下の図のように、鏡に線対称な図形を\(xy\)平面上に考えます。
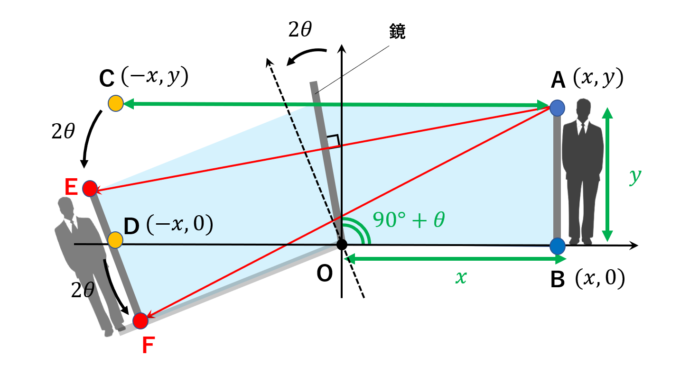
3.鏡の中の顔が身長の半分の位置のとき、全体を見渡せる
では、Xさんの目から鏡に映ったXさんの顔までの距離AEと、足元までの距離AFをそれぞれ求めていきます。そのために、まず各点の座標を決定しましょう。点C\((-x, y)\)、点D\((-x, 0)\)は原点中心に\(2\theta\)回転してそれぞれ点E、点Fになっていることから、回転行列の計算により、以下のように求まります。
\begin{align*}E=(-x\cos 2\theta-y\sin 2\theta,-x\sin 2\theta+y\cos 2\theta), F=(-x\cos 2\theta, -x\sin 2\theta)
\end{align*}
次に、ベクトルAE、AFを求め、その長さを計算しましょう。
\begin{align*}\vec{AE}&=\vec{OE}-\vec{OA}=
\left(
\begin{array}{c}
-x\cos 2\theta-y\sin 2\theta-x \\
-x\sin 2\theta +y\cos 2\theta-y
\end{array}
\right)\\
\vec{AF}&=\vec{OF}-\vec{OA}=
\left(
\begin{array}{c}
-x\cos 2\theta-x \\
-x\sin 2\theta-y
\end{array}
\right)
\end{align*}
であり、\(AE^2=AF^2\)であることから式を整理すると、以下のような等式が得られます。
\begin{align}
-x\sin2\theta+y\cos2\theta=y/2
\end{align}
この式から、鏡に映ったXさんの目の位置である点Eの\(y\)座標が\(y/2\)であることがわかります!つまり、鏡に映った自分の目の位置が、自分の高さの半分の位置であるとき、鏡に映る顔までの距離と足元までの距離が同じになることがわかります!
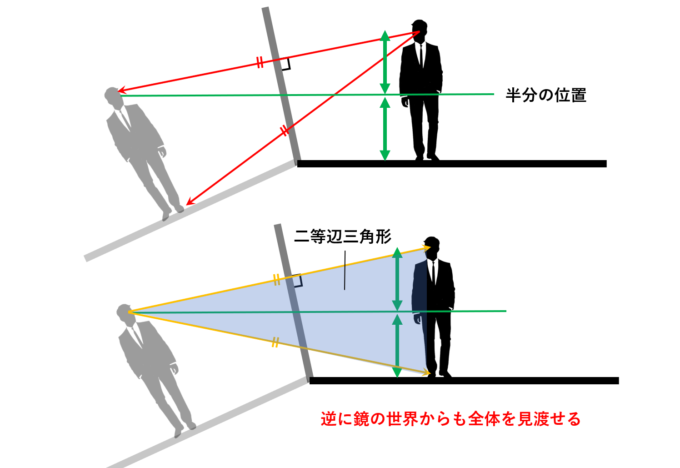
しかしこのことは、鏡の世界を中心に考えると実は当たり前だったりします…!まさにニーチェの「深淵をのぞく時、深淵もまたこちらをのぞいているのだ」状態です。しかし、実際に映っている顔の高さを測るのは難しいです。そこで、Xさんと鏡の距離が固定されているとし、鏡をどのくらい傾けたらいいかを考えてみましょう。鏡の下からXさんの目までの距離と傾きをそれぞれ\(r, \alpha\)とすると、点Aは\((x,y)=(r\cos \alpha, r\sin \alpha)\)と表すことができます。すると上の等式は
\begin{align*}
&r\sin \alpha \cos 2\theta-r\cos \alpha \sin 2\theta=y/2\\
\Longleftrightarrow &\sin(\alpha-2\theta)=\frac{1}{2}\sin \alpha\\
\Longleftrightarrow &\theta=\frac{1}{2}\left(\alpha-\arcsin\left(\frac{1}{2}\sin \alpha\right)\right)
\end{align*}
となり、\(\alpha\)が与えられたとき、ちょうどよい傾き\(\theta\)を求めることができます。例えば\(\alpha=45^{\circ}\)とします。このとき、関数電卓で計算してみると、\(\alpha=12.15^{\circ}\)と求めることができます。つまり、直角な鏡を\(12.15^{\circ}\)傾けることで、全体をバランスよく見渡せることができるのです!
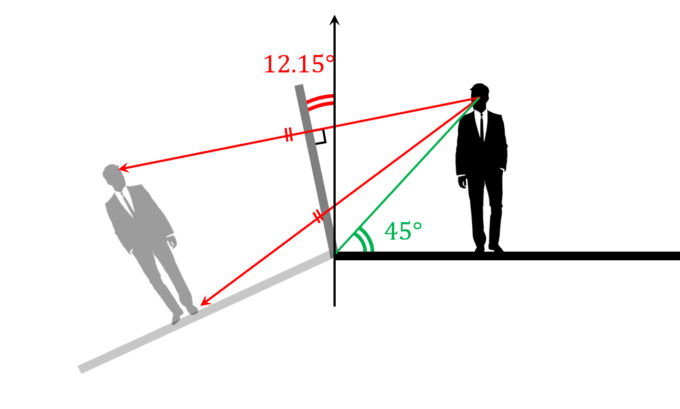
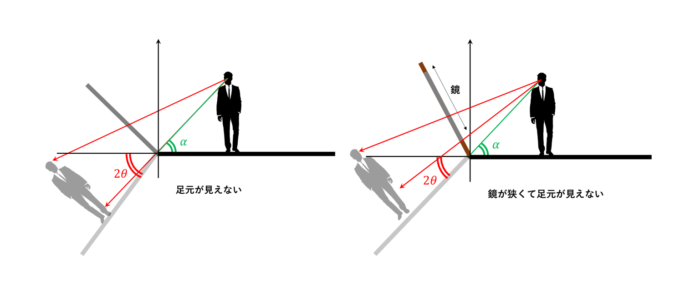
なお、補足ですが、\(\alpha-2\theta<0\)のとき、鏡で全体が見えなくなってしまいます。また、たとえ\(\alpha-2\theta>0\)であっても、下まで鏡になっていない場合は注意が必要です。
4.さいごに
いかがでしたでしょうか?ぶっちゃけると毎回こんな計算をしなくてもいい気はしますが、重要なのは数学を使うことで「最適な答え」を求められるという事実です!やはり数学は便利で美しいですね!
また、和からではオンラインによる集団授業や個別授業も行っております。算数から数学、統計学まで幅広く対応していますので、興味のある方はまずは無料の個別カウンセリングへ!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>
arttranson 全身ミラー 貼り付け鏡 姿見 フィレ フロートガラス 飛散防止 DIY式 枠無し (正方形30x30cm4枚)