皆さんこんにちは。和からの数学・統計講師の川原です。少し前になりますが因果関係についてのマスログの記事を書きましたが、本日はデータを用いて因果推論を行う上で気をつけなければならないとても不思議な現象をご紹介いたします。

よりよい治療法はどっち？

その不思議な現象とはシンプソンのパラドックスといい、1951年に統計学者のE. H. シンプソンによって提唱されました。
かんたんに言うとシンプソンのパラドックスとはある状況の下では分析のやり方によって矛盾した結果が出てしまうことがあるといった内容です。
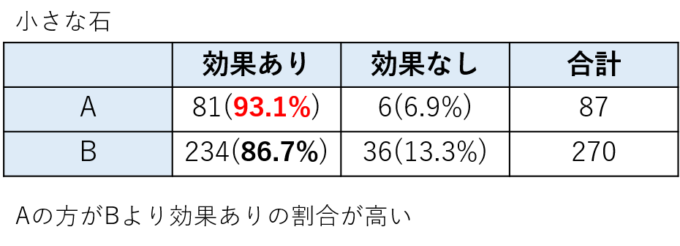
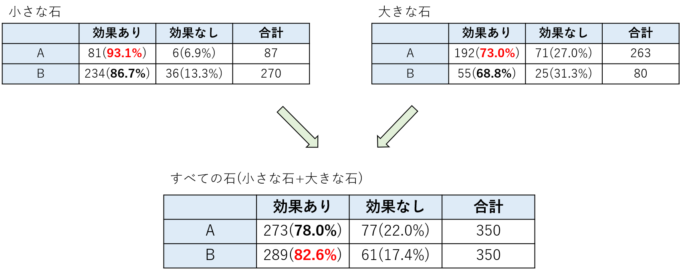
具体的な例でお話をしましょう。これは腎結石の2つの治療法AとBを比較した研究例です。腎結石に治療法にAとBのどちらが有効かを調べるため、2つの治療法の成功数を調べたものが下の表です。まずは石の大きさごとに2つの表を作っています。





この表をよく見てみましょう。まずは左の小さな石の表を見てみると、Aは87人中81人、つまり81/87=93.1%の人たちに効果がありました。一方Bは270人中234人、つまり234/270=86.7%の人たちに効果がありました。これから、小さな石ではAの治療法の方がよく効きそうだと思えます。





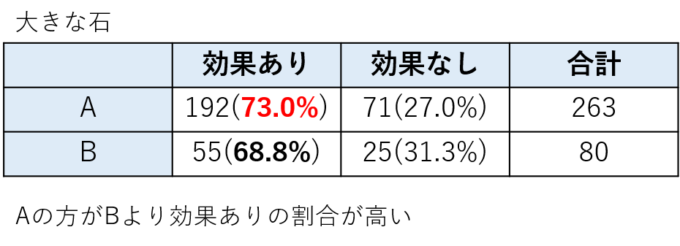
次に右の大きな石の表を見てみましょう。Aは263人中192人、つまり192/263=73.0%の人たちに効果がありました。一方Bは80人中55人、つまり55/80=68.8%の人たちに効果がありました。これから、大きな石でもAの治療法の方がよく効きそうだと思えます。





さて、ここからが問題です。それではこの2つの表をまとめて1つの表にしてみると次のようになります。

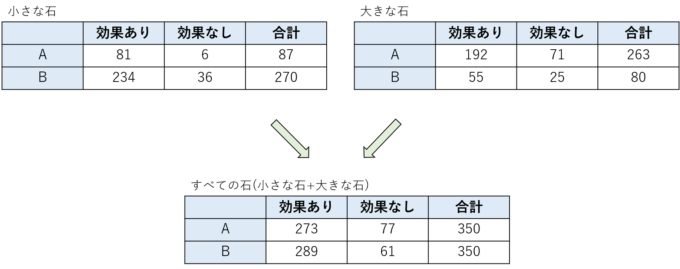
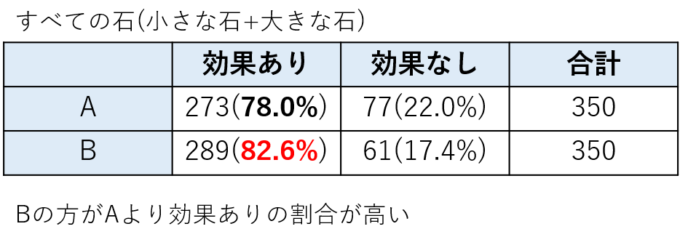
この表を見て治療法の効果を見てみましょう。Aは350人中273人、つまり273/350=78.0%の人たちに効果がありました。一方Bは350人中289人、つまり289/350=82.6％の人に効果がありました。これから考えるとBの治療法の方がよく効きそうです。





おや、おかしなことが起こりました。小さな石でも、大きな石でもAの治療法の方がよく効きそうですが、2つの表をまとめるとBの方がよく効きそうだという結果になってしまいました。このように、部分で考えた結果と全体で考えた結果が異なるという現象がシンプソンのパラドックスです。(すごく簡単に言うと)

どこがパラドックスなのか

全体の結果と部分の結果が異なるという結論は不思議な現象なのですが、実は数学的な視点で見ると上記の結果は不思議なものではありません。というのも、今回治療法の効果を割合という数学的指標を用いて表現していましたが、この割合という指標は

\begin{align*}\frac{A}{B} > \frac{a}{b} \end{align*}

\begin{align*}\frac{C}{D} > \frac{c}{d} \end{align*}

であっても、

\begin{align*}\frac{A+C}{B+D} > \frac{a+c}{b+d} \end{align*}

が必ずしも成立するとは限りません。つまりこの現象は数学的には何ら不思議ではない現象なのです。それが今回どこが問題だったかというと、この割合に治療法の効果という解釈を加えてしまったことです。このように数学的な指標に治療法の効果という因果的な解釈を与えてしまうと、矛盾をはらんだ表現になることがあります。

さいごに

それでは全体で見た解釈と、部分で見た解釈のどちらが正しいのでしょうか？実はこれに関しては状況によるというのが答えになります。
詳しい説明は省略しますが、治療法の効果という因果関係をデータから把握しようとした場合、データの数値だけで因果関係を把握することはできず、そのデータの構造によってどちらの結果が正しいかが変わってくるのです。シンプソンが論文を発表した当時は2つの解釈のうちどちらが正しいかはその状況によると伝えていますが、現在はこの因果推論の理論の整備が進み、上記の現象は「交絡」や「Collider」という言葉で説明ができるようになりました。(要するにどちらが正しいかを客観的な判断ができるようになっています)。この因果推論の分野はとても奥が深く、現在ではビジネスの世界でも効果測定などにこの分野が使われています。この分野に興味がある方はぜひ一度下記無料のセミナーにお越しください。

<文/川原祐哉>
⇒ 講師紹介ページへ

参考文献)
・統計的因果推論―回帰分析の新しい枠組み
統計的因果推論を数学をしっかり使って学んで行く本。読み進めるにはかなりの根気が必要ですが内容は良いです。