そのデータはどのくらい「すごい」のか？

統計・機械学習トピック

公開日

2017年5月17日

更新日

2017年5月17日

【初めて統計を学ぶなら無料オンライン講座開催中】

文系のための「統計超入門セミナー」-目で見てわかるビジネス統計学-

ある集団の中で何かを測定し、比較したとき、その一番上や一番下に来たものは明らかに「すごい」ものです。日本一高い富士山は日本一「すごい」山でしょうし、日本一広い琵琶湖は日本一「すごい」湖です。

では、一番上でも下でもなく、平均より少し上くらいに位置するものは、どの程度「すごい」のでしょうか？
その疑問に答えるのが、今回紹介する標準偏差です。

例として、小学5年生と中学2年生の握力を見てみましょう。スポーツ庁の調査によると、平成28年度の全国の小学５年生男子の握力は、次のようになっているそうです。
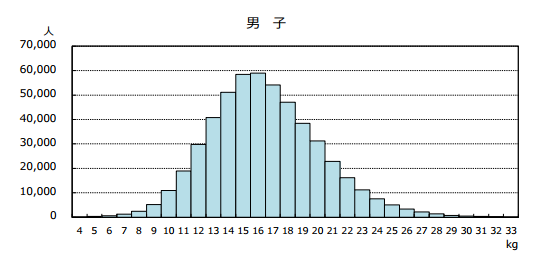（図1）小学5年生男子の握力
（『平成28年度全国体力・運動能力、運動習慣等調査報告書』平成28年、スポーツ庁より引用）

綺麗な山形になっており、平均は16.48 kgです。
もうひとつ、今度は中学2年生男子の握力の測定結果を見てみましょう。
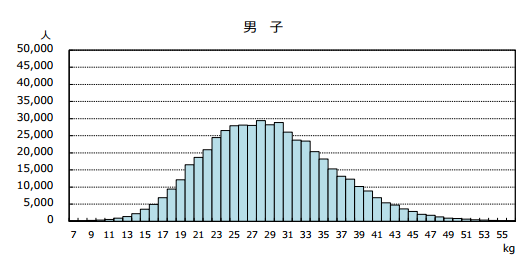（図2）中学2年生男子の握力
（同報告書より引用）

こちらも綺麗な山形で、平均は28.90 kgです。

この二つのデータを比較したとき、いったいどんなことが言えるでしょうか？
ひとつは、「中学2年生の方が、握力の平均が大きい」ということです。男の子は成長に従って、握力が増すようですね。

しかし、そんな当たり前のことしか言えないのでしょうか？　ほかに言えることはないでしょうか？

例えばここに、次のような二人の男の子がいたとします。

　A君：小学5年生で、握力 21.48 kg（小5男子の平均握力は 16.48 kg）
　B君：中学2年生で、握力 33.90 kg（中2男子の平均握力は 28.90 kg）

この二人は、どちらがより「すごい」のでしょうか？　単純な強弱で言えばB君の方が強いですが、平均と比較すると、どちらも平均より5 kg大きいだけです。そうすると、「すごさ」は同じなのでしょうか？

二つのグラフをよく見比べると、横軸の最小と最大が違うことに気付きます。
小学５年生の軸は4 ~ 33 kgですが、中学2年生の軸は7 ~ 55kgになっています。小学５年生より中学2年生の方が、横軸の幅が広そうですね。
つまり中学2年生の方が、握力のバラツキが大きいのだとわかります。

このバラツキ具合を、バシッとひとつの数値で表すのが、標準偏差です。

標準偏差の計算方法

標準偏差の計算方法を見せる前に、どうやったらバラツキの大小を表せるか、一緒に考えてみましょう。

一番単純な方法は、横軸の幅をそのまま書いてしまうことです。今回の場合だと、次のようになります。

　小学5年生　\(33 – 4 = 29 {\rm kg}\)
　中学2年生　\(55 – 7 = 48 {\rm kg}\)

これでバラツキを表せているでしょうか。今回の場合は良さそうですが、別のデータだったらどうでしょう。
例えば、9人で握力を測定した結果、こんなデータになったとします。これは、同じ方法でバラツキを表現できるでしょうか？
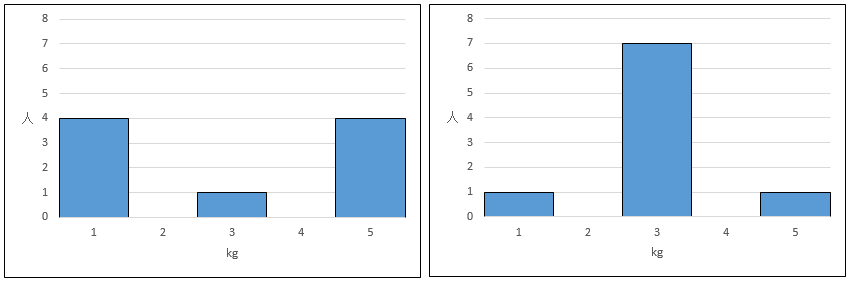（図3）横軸の幅では区別できない例

この二つのグラフは、どちらも横軸の幅は同じです。しかし、データのバラツキ具合は明らかに違います。左は両端に散らばり、右は真ん中に集中しています。データが散らばっている方がバラツキは大きいと考えられるので、左のバラツキの方が大きいと言えそうです。これをうまく区別しなくてはいけません。

そこで今度は、「各データで、平均との差を取る」という方法を考えてみましょう。平均との差のことを、「偏差」と呼びます。
図３のグラフはどちらも平均が 3 kg なので、各データの偏差は次の表のようになります。

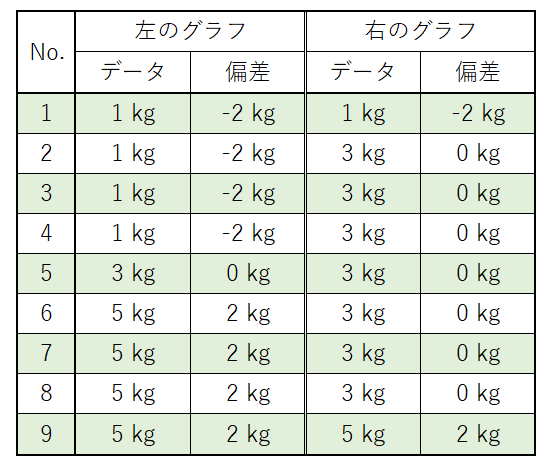（表１）図3のデータの偏差

しかしデータのバラツキを示すときに、いちいちこのような表を書くのは面倒ですし、あまり意味もありません。できれば平均のように、パッとひとつの値でバラツキを表現したいものです。
そこで、偏差をすべて足してみましょう。

　左のグラフ　\((-2) + (-2) + (-2) + (-2) + 0 + 2 + 2 + 2 + 2 = 0 {\rm kg}\)
　右のグラフ　\((-2) + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 2 = 0 {\rm kg}\)

……どちらもゼロになってしまいました。
これはデータが悪いのではなく、どんなデータでも偏差の和はゼロになることが知られています。

和をゼロにしないために、偏差をそれぞれ2乗してから足してみましょう。

　左のグラフ　\((-2)^2 + (-2)^2 + (-2)^2 + (-2)^2 + 0^2 + 2^2 + 2^2 +2^2 + 2^2 = 32 {\rm kg}^2\)
　右のグラフ　\((-2)^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 2^2 = 8 {\rm kg}^2\)

いい感じになってきましたね。バラツキの大きかった左が、大きな値を取っています。
しかしこのままでは、バラツキ具合が同じでも、データの個数が増えれば増えるほど、値も大きくなってしまいます。
そこで、データの個数が増えても値が大きくならないように、「1個あたり」で考えてみましょう。つまり、「偏差の2乗の平均」を考えるのです。そのために、さっきの値をデータの個数で割ってみましょう。

　左のグラフ　\(32÷9 = 約3.56 {\rm kg}^2\)
　右のグラフ　\(8÷9 = 約0.89 {\rm kg}^2\)

これなら、データの個数が増えても、値はあまり変わらなさそうです。
しかし、元のデータの単位が \({\rm kg}\) だったのに、ここでは \({\rm kg}^2\) などという見慣れないものになっています。偏差を2乗したからですね。
そこで、これのルートを取ることにしましょう。

　左のグラフ　\(\sqrt{約3.56} = 約1.89 {\rm kg}\)
　右のグラフ　\(\sqrt{約0.89} = 約0.94 {\rm kg}\)

これで単位も元に戻って、すっきりしました。
そして、これが標準偏差の計算方法です。

標準偏差は、「各データの平均との差を、2乗して、足して、データの個数で割り、ルートを取った値」なのです。

標準偏差と「すごさ」の関係

計算方法はわかりました。でもこれは、一体何を意味する値なのでしょうか？
もちろん、「データのバラツキ」を意味する値です。しかしもう少し具体的な意味があります。

標準偏差は、偏差が大きいデータが多いのか、小さいデータが多いのかを表す値なのです。

　標準偏差が大きい　→　偏差が大きいデータが多い
　標準偏差が小さい　→　偏差が小さいデータが多い

と読み解くことができるわけです。

実は最初の握力の測定結果では、標準偏差がそれぞれ、

　小学5年生の標準偏差　3.76 kg
　中学2年生の標準偏差　7.14 kg

となっていました。中2男子の方が、平均から離れた握力の持ち主が多い、ということですね。このことから、例えば「小５までは全員同じように筋力を伸ばすが、思春期に入ると運動習慣の違いが如実に握力の差となって現れる」のように解釈することができます。
（これは筆者がいま考えついた解釈です。ちゃんとした理由は、然るべき方法でお調べください）

標準偏差がわかると、他にもわかることがあります。
それは、「あるデータが、どのくらい特別なのか？」ということです。

ようやく、最初の二人について考えられるときが来ました。この二人は、どちらが「よりすごい握力の持ち主」と言えるでしょうか？

　A君：小学5年生で、握力21.48 kg（小5の平均は16.48 kg、標準偏差は3.76 kg）
　B君：中学2年生で、握力33.90 kg（中2の平均は28.90 kg、標準偏差は7.14 kg）

結論から言うと、この二人ではA君の方が「よりすごい握力の持ち主」と言えます。
なぜでしょうか？

それは、小5の標準偏差の方が小さいからです。

標準偏差が小さいということは、より多くのデータが平均付近に集まっているということです。そのためA君は、「集団の中で群を抜いて強い」と言えます。
一方、中2は標準偏差が大きいので、平均から離れたデータもたくさんあります。そのためB君は、「群の上の方」に留まっているにすぎません。
だから、A君の方が「よりすごい握力の持ち主」と言えるのです。

……この説明は、言葉だけだと少しわかりにくいかもしれません。グラフを使って、もう少し細かく説明しましょう。

正規分布と標準偏差の関係

マスログでは以前、平均の記事で、「グラフが正規分布になると、ちょうどド真ん中が平均になる」と紹介しました。正規分布とは、次のような形のグラフのことです。
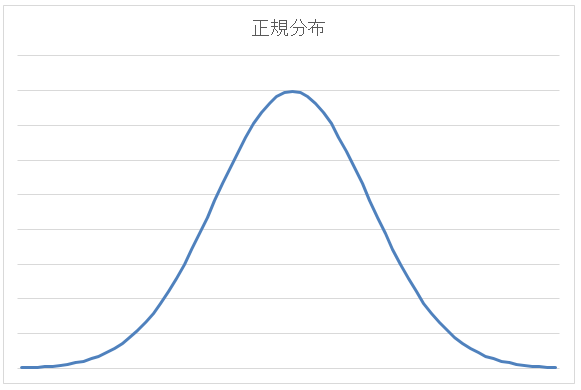（図4）正規分布

平均と正規分布に特別な関係があったように、標準偏差と正規分布にも特別な関係があります。
正規分布のグラフに、平均と標準偏差を書き込んでみましょう。
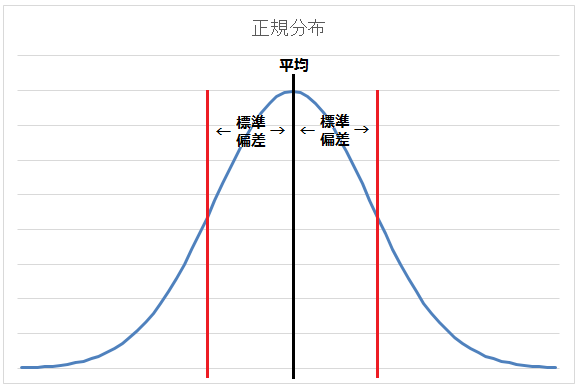（図5）正規分布と標準偏差

真ん中の黒い線が平均で、その両側に標準偏差だけ離して赤い線を引きました。
実は、データが正規分布に従う場合、全データのうち約68%が赤い線の内側に入ることが知られています。
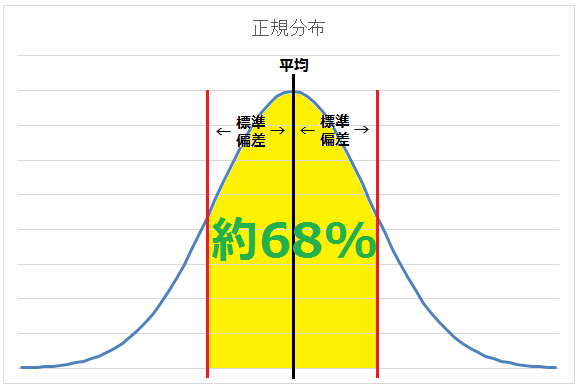（図6）平均±標準偏差の範囲内に、全データの約68%が入る

見方を変えると、平均から標準偏差までのデータは、全体の約34％ということになります。また、平均より下のデータは全体の50％です。これらをグラフに書き込むと、こうなります。
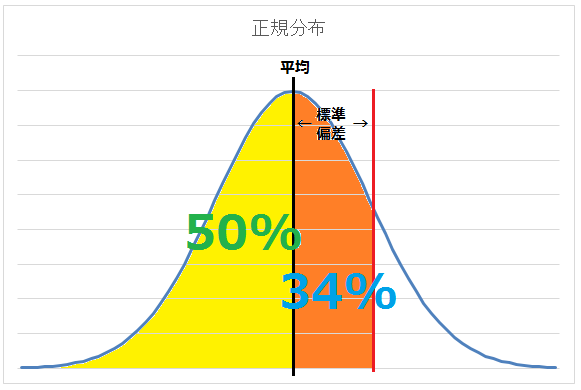（図７）平均以下は50％、平均から標準偏差までは約34％

ところで、最初の握力の測定結果のグラフは、正規分布に非常に近い形をしていました。ここで、もう一度あの二人を見てみましょう。

　A君：小学5年生で、握力21.48 kg（小5の平均は16.48 kg、標準偏差は3.76 kg）
　B君：中学2年生で、握力33.90 kg（中2の平均は28.90 kg、標準偏差は7.14 kg）

二人とも、偏差が +5 kgの握力の持ち主です。
しかし、小5の標準偏差は3.76 kgなので、A君の偏差は標準偏差以上あります。従って、A君は小学5年生全体の84％よりも強い握力の持ち主であることがわかります。
一方、中2の標準偏差は7.14 kgなので、B君の偏差は標準偏差以下です。従って、B君は中学2年生全体の84%以内の握力しか持っていないことがわかります。

このことから、A君の方が「（同学年の子と比較して）よりすごい握力の持ち主」と言えるのです。