データ利用・活用超入門-データを情報に変える統計学-

「日本のサラリーマン世帯の平均月収は、約52万円」
というデータをご存知でしょうか。総務省が集計した2014年のデータです。

「月収52万円！？　そんなに！？」と驚く人もいるかもしれません。平均値というのは、ふつう、データ全体の様子を表す値です。それがこんなに高いなんて……と思われるかもしれません。

しかし近年の統計ブーム(?)のおかげか、こういったデータのカラクリを知っている人も増えてきました。そして、そのカラクリを知っている人は、誰もが口をそろえて言います。
「平均は当てにならない」
と。

でも、それは本当でしょうか。平均といえば、統計における基本中の基本の概念です。それが疑わしいなんてこと、あるのでしょうか。

今回の記事は、そんな平均のお話です。

平均が使えない場合

さてまずは、平均月収のデータのカラクリを明かしましょう。結論から言うと、これは「上位の人たちが平均を押し上げている」ために起こる現象です。

平均は、すべてのデータの値を足した後、データの個数で割って求めます。このとき、いくつかのデータが極端に大きいと、平均も極端に大きな値を取ってしまうのです。

試しに、「１人あたりの銀行預金残高」の都道府県別の平均を見てみましょう（2014年、総務省）。

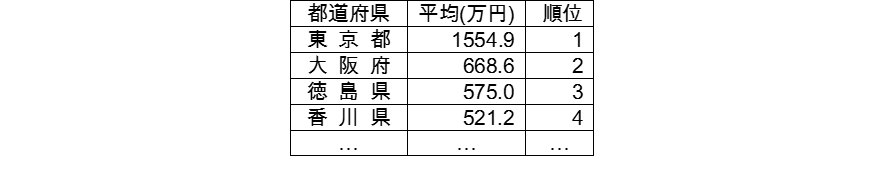
明らかに、東京都だけ大きすぎますね。これは、度数分布表というグラフにするとよりはっきりします。

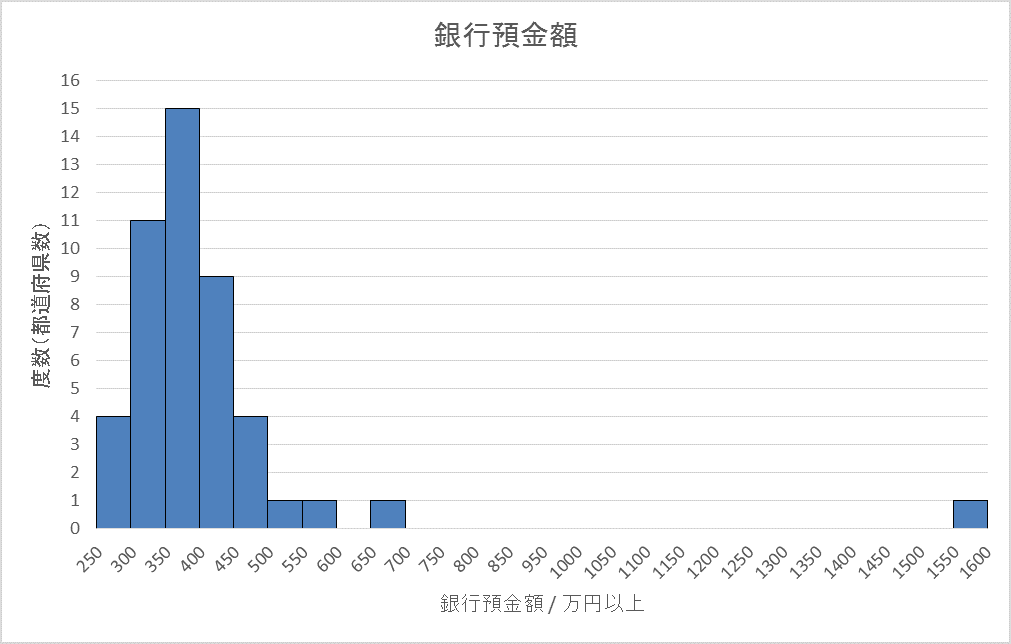
このグラフは、横軸に各都道府県の1人あたりの平均預金額を、縦軸にその金額の都道府県がいくつあるかを表したものです。たとえば、平均預金額が250万円以上300万円未満の都道府県は、全国に4つあることがグラフから読み取れます。

さてこのグラフを見ると、随分左に寄っています。そして右の方に、ちょこんと1つだけ棒が出ています。これが東京都ですね。

このグラフを見たとき、「平均はどこか」と聞かれたら、おそらく多くの人は、このあたりにあるだろうと考えるでしょう。

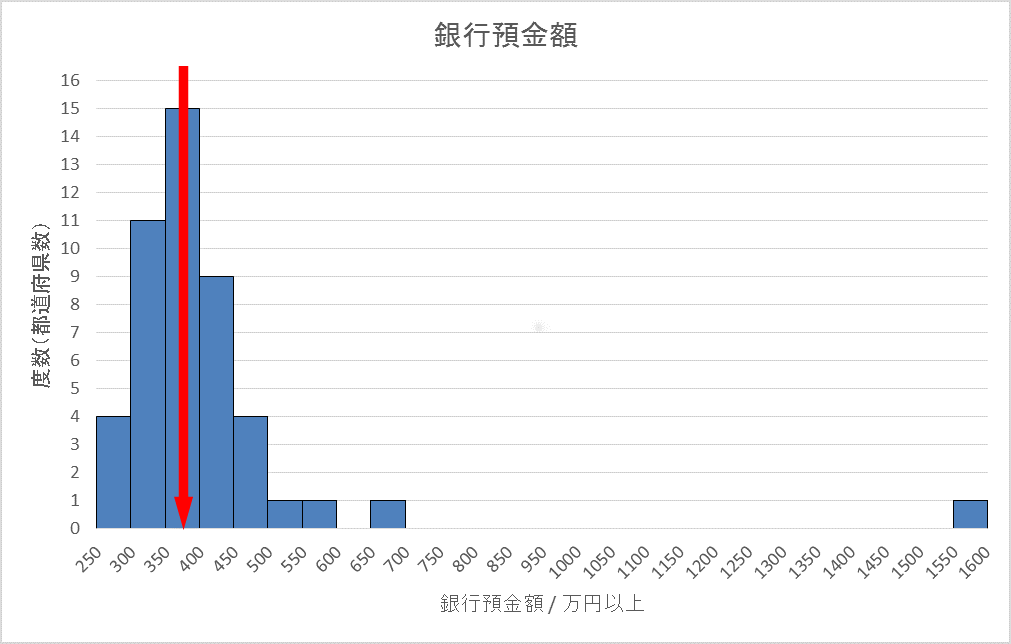
ところが、実際にこの47都道府県の平均を計算してみると（つまり、全部足して47で割ってみると）、411万円になります。従って、矢印の場所はもう少し上になります。

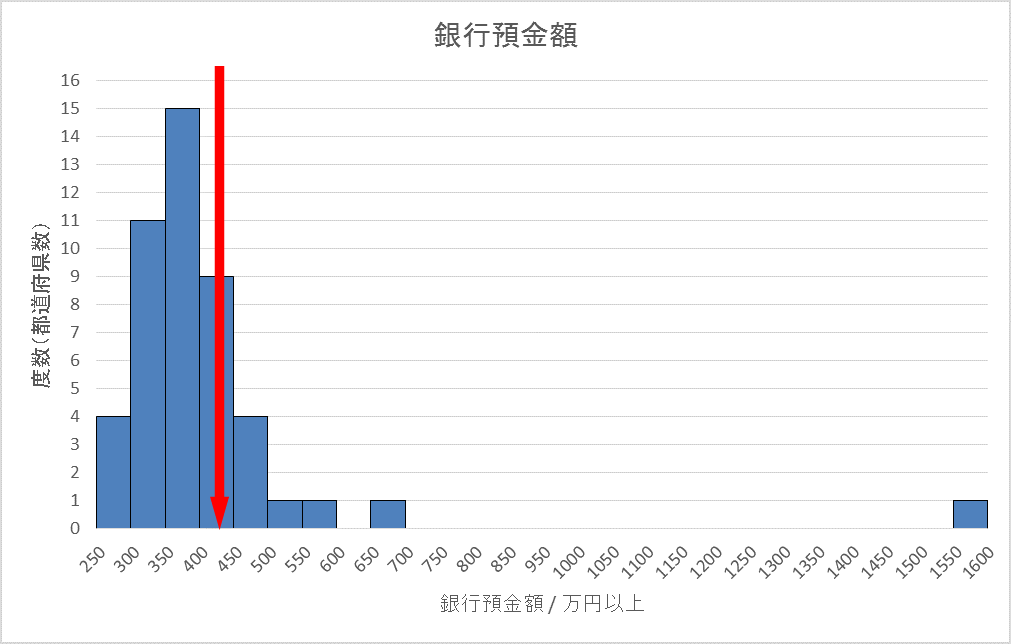
47都道府県のうち、「平均」より上にあるのは15。これは全体のたった3割にすぎません。逆に言えば、全体の7割近くが平均より下にあることになります。

普通、「平均」と聞いてイメージするのは、「なんとなく真ん中あたりの値」です。しかし上の図から明らかな通り、極端に大きな（または小さな）値があると、平均は真ん中あたりからずれてしまうのです。

平均が使える場合

このように、平均には大きな落とし穴があるのです。

昨今の統計ブームのおかげか、平均のこの落とし穴を知る人が増えました。そこで、平均を見たらとりあえず疑う、いわば平均懐疑主義のような人たちも増えています（※筆者の偏見です）。

ですが、平均でちゃんと全体像を表せる場合もあります。その一例をご紹介しましょう。

そもそも、月収や預金額の平均が当てにならないのは、極端に大きな値が存在するからです。ですから、そのような値がほとんど存在しないデータなら、その平均は信頼するに足ります。

例えば、次のデータはどうでしょうか。

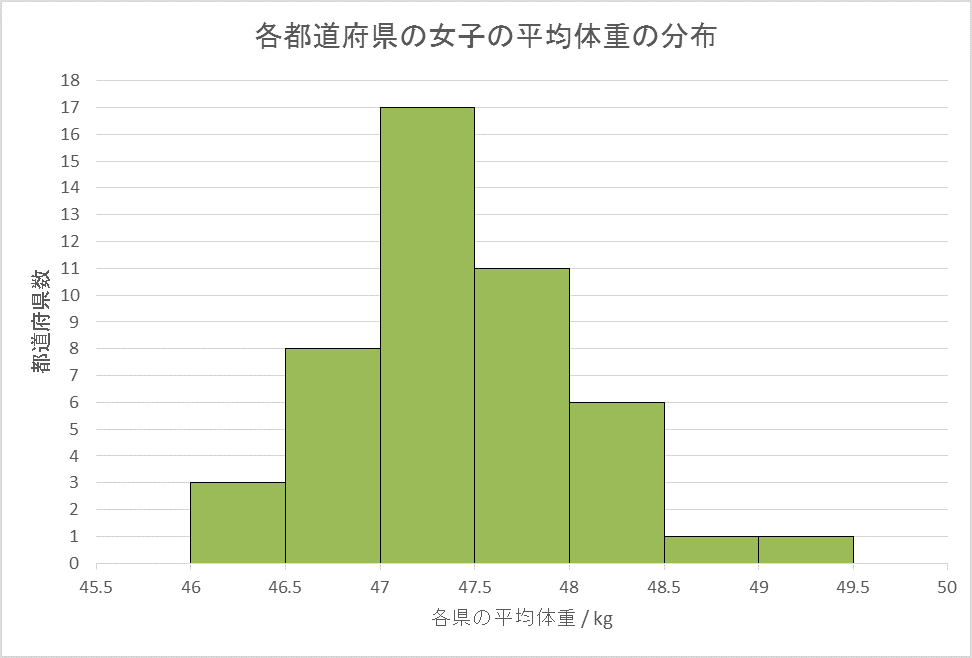
これは、中学2年生の女子の平均体重を、都道府県別にまとめたものです（2014年、総務省）。このグラフを見ると、例えば平均体重が46 kg以上46.5 kg以下である都道府県は３つであることがわかります。

このグラフには、極端に大きな値も、極端に小さな値もありません。なので平均を取れば、ほとんど真ん中あたりに来るはずです。

では計算してみましょう。各都道府県の平均体重を足し、それを47で割ります。
すると、47.4 kgという値が得られます。

平均より上の都道府県は21、下は26なので、感覚的に「ほとんど真ん中」と言ってよさそうな値が得られました。

このグラフのように、真ん中が一番高く、左右に行くにつれ少しずつ減っていくデータであれば、平均はグラフの一番高いところの値に近づきます。そして、正規分布と呼ばれる以下のようなグラフになると、両者は完全に一致します。

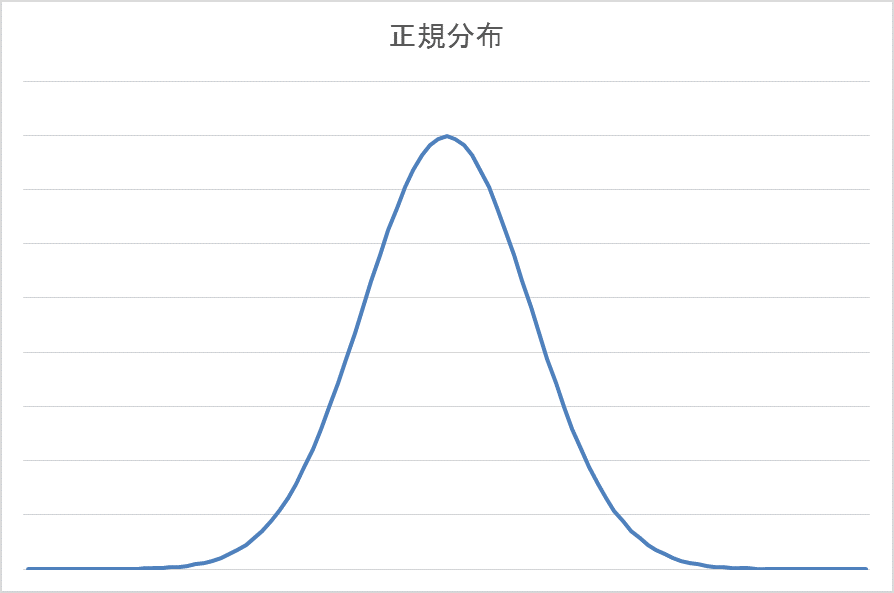
グラフの形が正規分布に近ければ近いほど、平均の値は私たちがイメージずる「平均」に近づいていくのです。

というわけで、まとめです。

平均だけに注目すると、極端なデータがあるときに、全体像を見誤ってしまいます。
しかし、極端なデータがないことさえわかっていれば、平均は全体像を掴むのに十分役立つ値です。

重要なのは、「このデータは平均が使えるデータなのかどうか」をきちんと見極めることなのです。

［参考資料]：総務省/統計でみる都道府県のすがた(記事は2016年度版を参照)

（文／キグロ）