革命的掛け算(2桁×2桁)のやり方を伝授します【インド式】[youtube公開]
公開日
2022年11月10日
更新日
2025年9月16日

みなさんこんにちは、大人の数トレ教室の堀口です。
今回は\(96\times92\)を\(3\)秒で計算する方法についてお話ししていきたいと思います。
この方法を知っていれば\(2\)桁の掛け算の考え方が一気に変わると思います。

この記事の主な内容
インド式計算の方法
みなさんは\(96\times92\)の計算を\(3\)秒でできますか?
そろばんなどで計算の練習をしていないとちょっと難しそうですよね。
この計算の答えは\(8832\)なのですが、この答えを\(3\)秒で導くことができる方法を紹介します。
どんな流れかを説明していきます。
まずは\(96\)と\(92\)のそれぞれから\(100\)を引きます。そうすると差は\(-4、-8\)になります。
このように\(100\)との差を出すことができればあとは簡単です。
出てきた\(2\)つの差をかけた数を右側に、\(96\)と\(92、-4\)と\(-8\)を交差するように足し算したものを左側に置きます。
左側は\(2\)つとも同じ数字になります。

あとはこの\(2\)つの数字をくっつけるだけで、\(8832\)という答えが求まります。
これがインド式の掛け算の計算方法です。この方法は基本的に\(100\)に近い\(2\)桁の数の掛け算をするときに使いやすいと思います。
インド式計算を使った計算の例
それではもう一つ別の問題を見てみましょう。

これも\(100\)に近い数の掛け算になっているので、インド式計算を使って計算してみましょう。
まずはそれぞれから\(100\)を引くと、

と2つの数字が出ます。
右側には\(-2\)と\(-13\)を掛け合わせた\(26\)が入ります。
左側には交差する数を足し合わせた\(85\)が入ります。
(どちらの組を足し合わせても同じ数になるので、どちらか一方だけを計算すればよいです。)
最後に、\(85\)と\(26\)をくっつけた\(8526\)が答えになります。

このように簡単な計算だけで、あとはそれらをくっつけるだけで簡単に計算することができるんですね。
インド式計算を使った計算の例(その2)
それではもう\(1\)問インド式計算を使って計算問題にチャレンジしてみましょう。
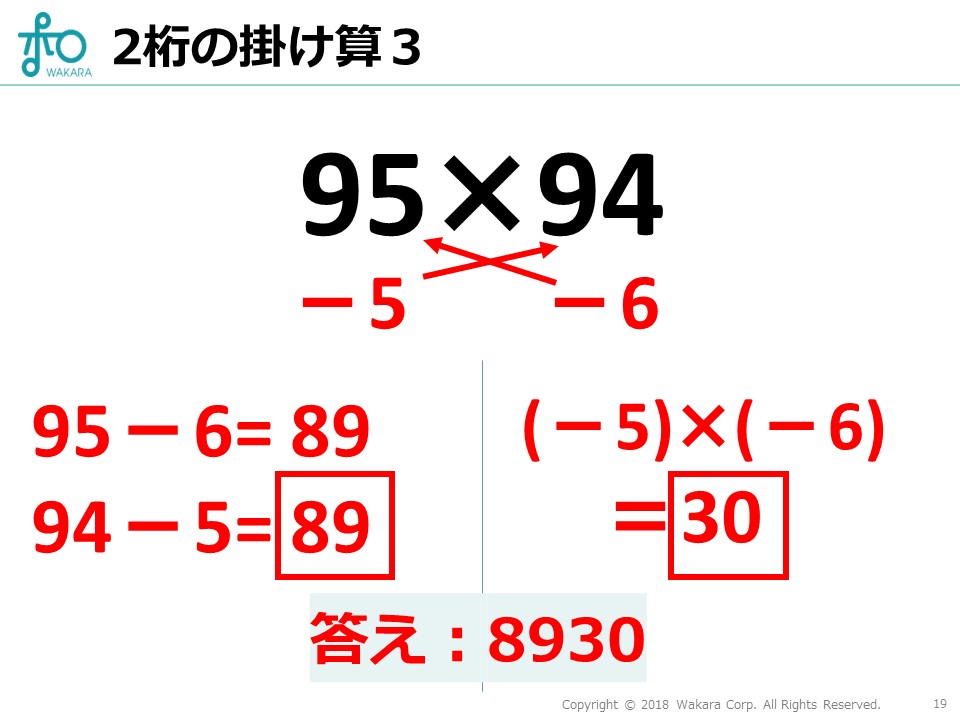
例えば、\(95\times94\)はどんな答えになるでしょうか。インド式計算を使って頭の中で計算してみてください。
インド式計算を使ってうまく答えが出せましたか?
それぞれから\(100\)を引いた数同士をかけた\(30\)を右側に、交差して足し合わせた\(89\)を左側にすれば、答えが\(8930\)と一瞬で答えが求まります。
\(100\)より大きい数でのインド式計算
実は、インド式計算は\(100\)より大きい数同士の掛け算でも使うことができます。
例えば、\(105\times104\)を計算してみましょう。手順は前の時と同じです。
まずは\(2\)つの数それぞれから\(100\)を引くと\(+5\)と\(+4\)が出てきます。
これをそれぞれ掛け合わせると\(5\times4\)で\(20\)となり、右側には\(20\)が入ります。
そして左側には\(105\)と\(4\)を足し合わせた\(109\)が入ります。そうすると、\(109\)と\(20\)をくっつけると\(10920\)になります。

なんとこれが\(105\times104\)の答えになるんです。
それではこの計算を踏まえてもう\(1\)つ問題を解いてみましょう。
次は\(111\times103\)をインド式計算を使って計算してみましょう。
すぐに計算できましたかね?
それぞれの数から\(100\)を引くと\(+11\)と\(+3\)となります。
なので、右側には\(11\times3\)で\(33\)が入り、左側には交差した\(111\)と\(3\)を足し合わせて\(114\)が入ります。

あとはこれらの数をくっつけて\(11433\)が答えになります。
インド式計算のまとめ
それではこれまでのインド式計算の仕方を最初に計算した\(96\times92\)の計算を例におさらいしてみましょう。
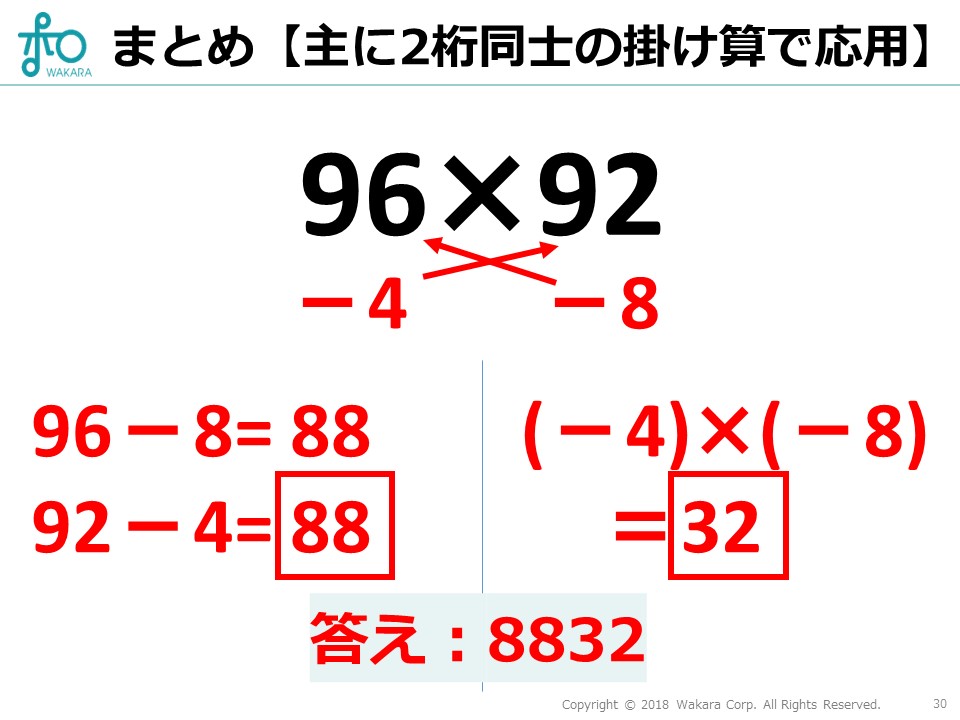
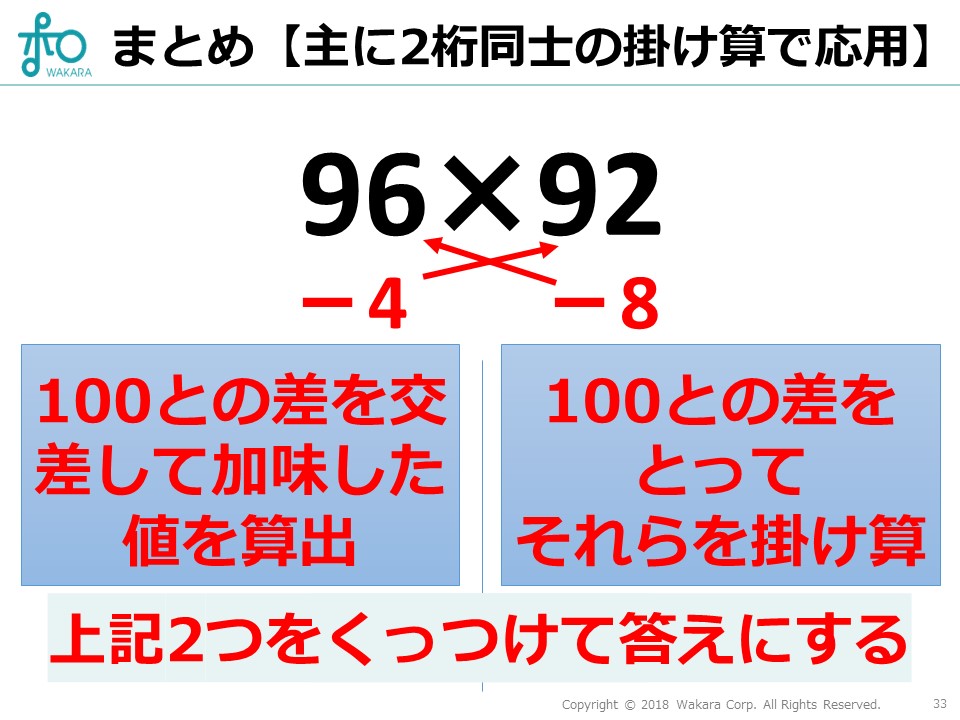
まず初めにそれぞれから\(100\)を引きます。
その差同士を掛け算したものを右側に、交差して足し合わせた値を左側に置きます。
あとはこれらの出てきた数をくっつければ、簡単に答えが出ます。
このような計算で\((2桁)\times(2桁)\)の計算ができたわけです。ぜひ、応用してみてください。
インド式計算の応用
このインド式計算法は\(2\)桁同士の掛け算で使いやすいのはもちろんなんですが、実は応用すれば\(3\)桁以上でも\(1\)桁でも使うことができます。
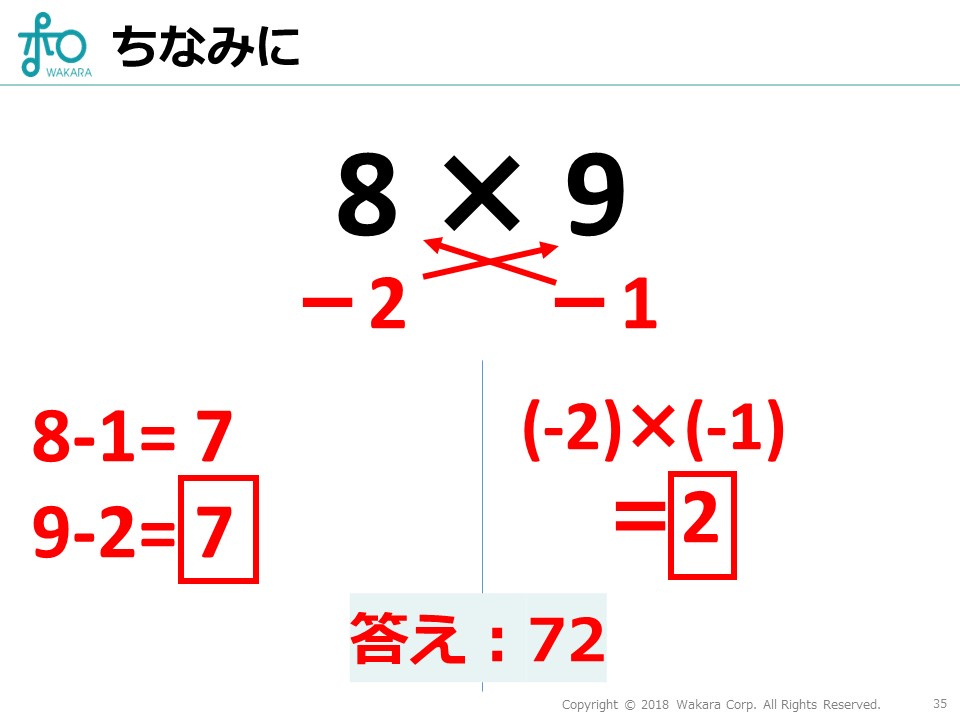
例えば、\(8\times9\)の計算をインド式計算の応用を使って計算してみましょう。
もちろん九九を覚えていれば答えは\(72\)とわかるのですが、ここでそれぞれから\(10\)を引いてみます。
そうすると\(-1\)と\(-2\)が出てきます。これらを掛け合わせた\(2\)を右側に、交差して足し合わせた\(7\)を左側に置いて\(7\)と\(2\)をくっつければ\(72\)になりますよね。
このように適切に引く数を変えていけば簡単に応用することができます。
桁が大きくなると計算が大変になってインド式計算を使う意味がなくなってしますのですが、生活のちょっとした時や受験などの適切なタイミングでぜひ活用してみてください。
YouTubeでは、より詳しくインド式計算について解説しているのでぜひご覧ください。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/堀口智之>















