空間図形（立体）とは

↓↓↓動画で見たい方はこちら↓↓↓

空間図形（立体）とは、円や三角形などのような平面図形に「高さ」が加わったような図形のことです。例としては、円に高さを加えた円柱や三角形に高さを加えた三角柱、立方体などがあります。前回は多面体である直方体と立方体について、そして、頂点や辺、面などの言葉の説明をしました。今回は三角形を使った空間図形について考えていきたいと思います。
前回の記事はこちらになりますのでぜひご覧ください。
（参考：空間図形（立体）の総復習（直方体・立方体編）【算数からやさしく解説】）

三角柱について

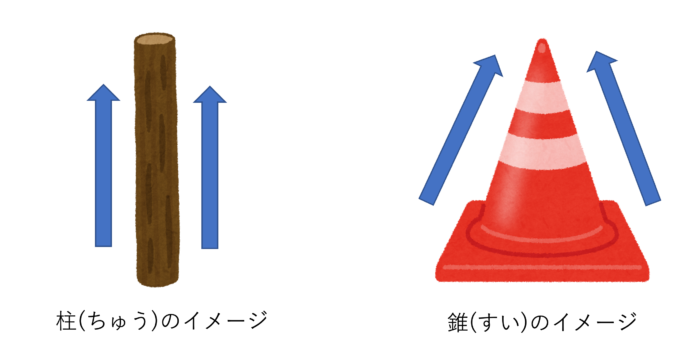
立体についての説明の前に「柱（ちゅう）」と「錐（すい）」についてのイメージについて説明したいと思います。「柱」というのは、「はしら」と読むように、上にふたと下に底があるような棒のようなもののイメージです。それに対して、「錐」というのは三角コーンのように下に底はあっても上がすぼまっているような形のものです。

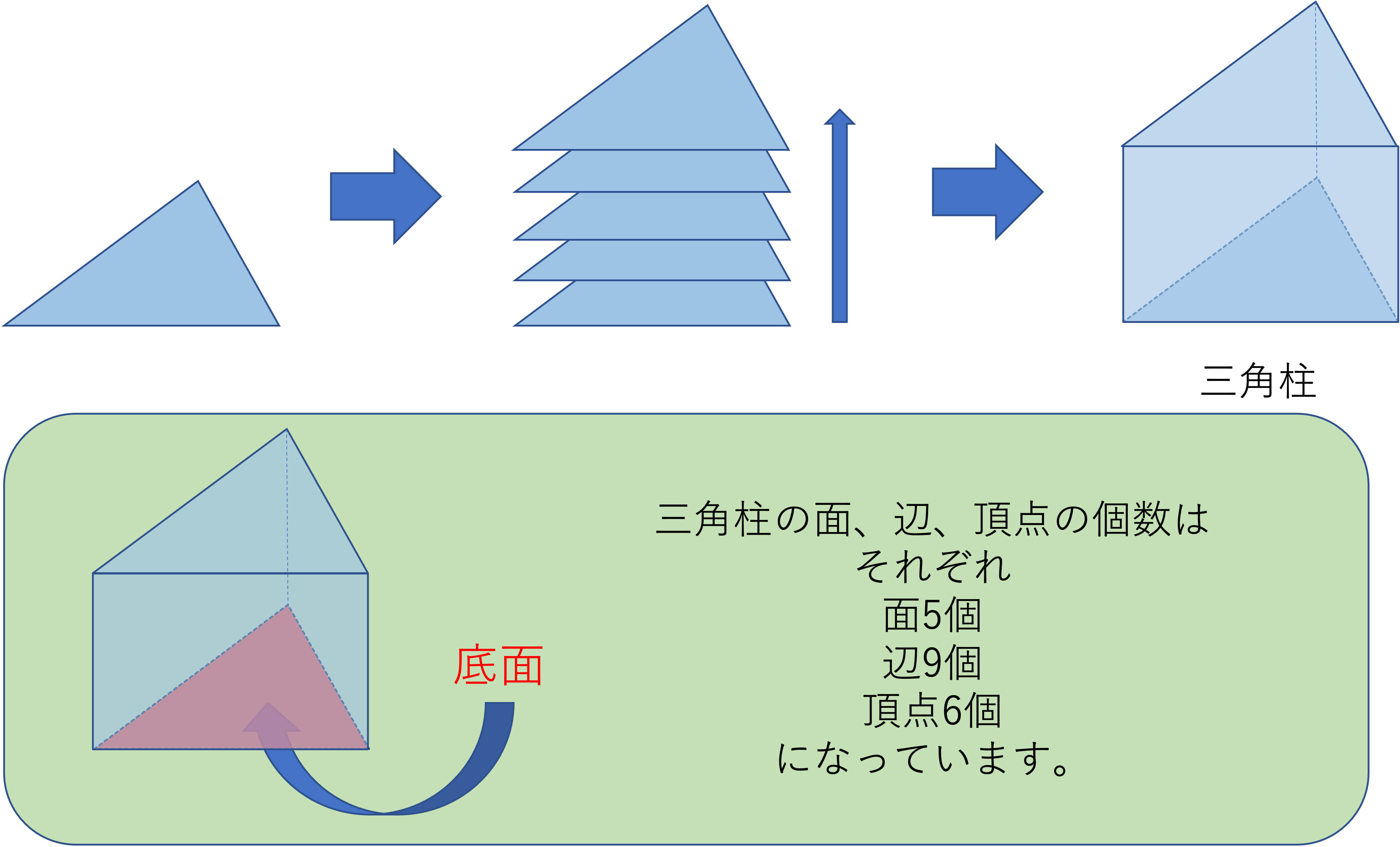
ここで三角柱について考えてみましょう。三角「柱」なので、これは図のように同じ形（合同）な三角形が、上と下にそれぞれ同じ向きでふたと底として付けられているような立体になります。
前回のように、平面上の三角形を“高さ”の方向に伸ばすような考え方でも同じような形の立体になると思います。

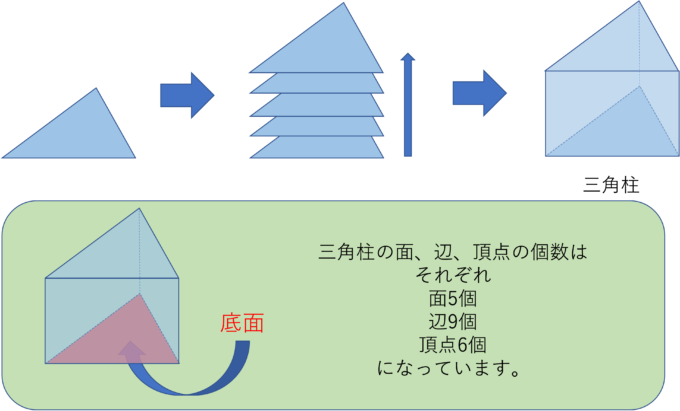
この時、底にした三角形のようにその立体の底になっている面を「底面」と言います。
（反対側を底だと考えればそちらの面が底面になるので上の面も底面と呼ぶことがあります。）
三角柱もすべての面が平面なので多面体の1つで、頂点、辺、面の数はそれぞれ６個、９個、５個になります。

三角錐について

続いて三角「錐」になりますが、先ほどもいったように「錐」というのは三角コーンのように下に底はあっても上がすぼまっているような形のもののことです。
したがって三角錐の形は下図のようになります。

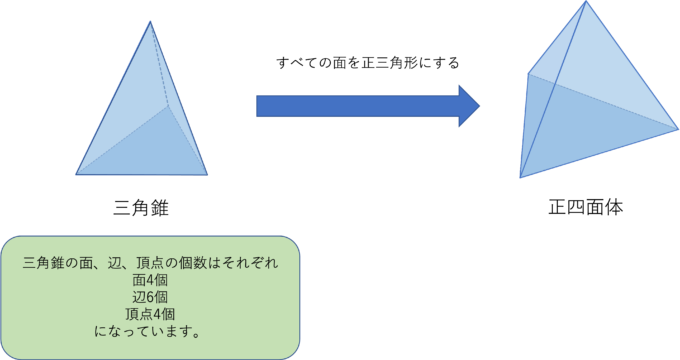
この図からもわかるように、三角錐は４つの三角形に囲まれています。また頂点、辺、面の数はそれぞれ４個、6個、４個になっており、三角柱と三角錐ではパッと見た時の形だけでなく、実際に頂点や辺、面などの数が違うことからも別の空間図形であることがわかります。
前回解説したように、直方体のすべての面が正方形であるようなものが立方体だったのに対して、三角錐の４つすべての面が正三角形あるような立体のことを正四面体と言います。

三角柱や三角錐の活用例

今回は三角形を底面にするようなもので柱のようなものには三角「柱」、片方がすぼまっているようなものには三角「錐」とつけましたが、今後扱っていく立体では、底辺が三角形ではなく四角形や円であるものを考えていきます。
また、これらの立体の体積を求めるときに、「柱」の形であるものと「錐」の形であるものによって体積の計算が少し変わってくるので、そのような意味でもここでこれらの区別を確認することは大切です。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

空間図形（立体）の総復習（直方体・立方体編）【算数からやさしく解説】

<文/尾崎>