↓↓↓動画で見たい方はこちら↓↓↓

みなさんこんにちは。和からの数学講師の伊藤です。前回のマスログでは、2000年に静岡大学で出題された入試問題をご紹介しました（前回の記事はこちら）。問題に従ってグラフを書いてみると富士山の形になるという、とても遊び心のある問題でした。…しかし、山梨県出身である私は、羨ましいと思いつつも、こんなことを考えてしまいました。「静岡大学の受験生には、静岡から見た富士山を書いてほしい！」と。そんなわけで今回は、この入試問題をより静岡大学らしい問題に勝手にアレンジしてみようと思います。

１．静岡大学から見た富士山って…

まずは前回ご紹介した問題と、その解答をおさらいします。

関数$f(x)$,$g(x)$を

$$\begin{align*} f(x) &= \left\{ \begin{array}{ll} x^4-x^2+6 & (|x| \leq 1)\\ \frac{12}{|x|+1} & (|x| > 1) \end{array} \right.\\ g(x)&=\frac{1}{2}\cos (2\pi x)+\frac{7}{2} \hspace{1.0em}(|x|\leq 2) \end{align*}$$

で定義する。このとき、次の問いに答えよ。

(1) $f(x)$,$g(x)$の増減を調べ、2曲線$C_1:y=f(x)$,$C_2:y=g(x)$のグラフの概形を同じ座標平面上にかけ。
(2) $C_1$,$C_2$で囲まれた部分の面積を求めよ。

(1)の問題の通りグラフを書いてみると、このようになりました。

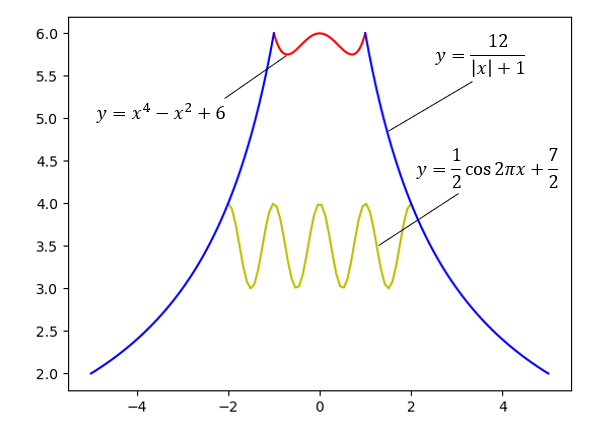
綺麗な富士山が出てきましたが、実は静岡県側から富士山を見てみると、こんな風に見えるのです。

右側に盛り上がった部分が見えます。これは宝永山といって、約300年前の大噴火でできた山とされています。せっかく静岡大学を受験された受験生の皆さんには、ぜひこの山まで再現していただきたい…ということで今回、この宝永山も再現した問題を考えてみました。

２．発想

※この章は難しい内容になるので、読み飛ばしていただいても構いません。

まず、これから作るオリジナル問題には指数関数を組み込みたいと思いました。元の問題が高校数学の広い範囲を網羅していたため、ここに指数関数が入れば高校数学の重要な関数をほぼすべて盛り込めると思ったからです。
それから宝永山の部分は、関数$f(x)$に別の関数を合成することで再現しようと思いました。つまり、関数$h(x)$を用いて、$f\circ h\left(x\right)$という形の合成関数で宝永山を表現していきます。$f(x)$を定義している領域をもっと細かく分けても良いのですが、そうすると関数が煩雑になってしまうのではないかと思ったためです。

このように考えると、$f(x)$に合成する関数$h(x)$の条件が見えてきます。
・指数関数を含む。
・宝永山を作りたい位置では$f(x)$は単調に減少するため、合成関数$f\circ h\left(x\right)$を盛り上がった形にするためには、その位置で$h(x)$は谷の形になっている必要がある。
・$3 < x < 5$の範囲だけ形を変えることにするのであれば、それ以外の範囲では$h(x)=x$とすればよい。また$3 < x < 5$の範囲では$xe^○$といった形にして、○の部分は$x=3$と$x=5$で$0$になるように調整する。これで$f\circ h\left(x\right)$が連続になる。

ここまでの内容を踏まえて、実際に関数$h(x)$を考えてみました。

３．宝永山を再現した問題

では、さっそく関数$h(x)$を導入した問題を見てみましょう。

関数$f(x)$,$g(x)$,$h(x)$を

$$\begin{align*} f(x) &= \left\{ \begin{array}{11} x^4-x^2+6 & (|x| \leq 1)\\ \frac{12}{|x|+1} & (|x| > 1) \end{array} \right.\\ g(x)&=\frac{1}{2}\cos (2\pi x)+\frac{7}{2} \hspace{1.0em}(|x|\leq 2)\\ h(x) &= \left\{ \begin{array}{ll} xe^{\frac{1}{3}(x^2-8x+15)} & (3 < x < 5)\\ x & (x \leq 3, 5 \leq x) \end{array} \right.\\ \end{align*}$$

で定義する。このとき、次の問いに答えよ。

(1) $f \circ h(x)$,$g(x)$の増減を調べ、2曲線$C_1:y=f \circ h(x)$,$C_2:y=g(x)$のグラフの概形を同じ座標平面上にかけ。

ここで導入した$h(x)$は、確かに先ほど挙げた条件を満たしています。$e$の指数部分に$\frac{1}{3}$とありますが、この部分で宝永山の高さを調整しています。このグラフを実際に書いてみると、次のようになります。

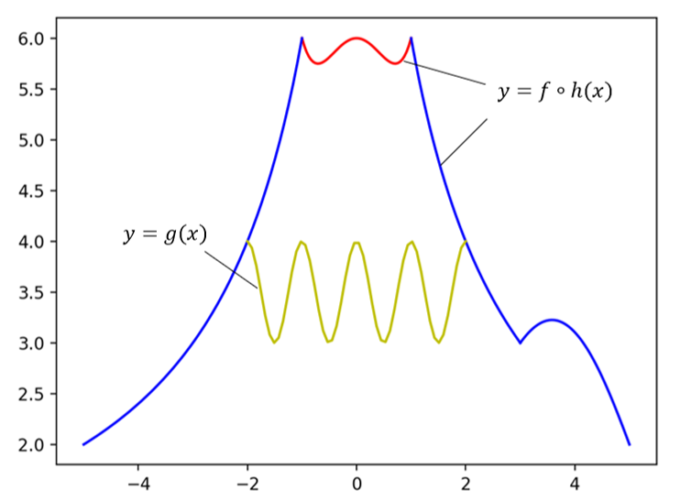
なかなかそれらしいグラフが出てきました。無事宝永山が再現できてめでたしめでたし…と思ったのですが、先ほど書いたグラフを弊社スタッフの岡本に見せたところ、「変曲点が欲しいね。」と言われてしまいました。どういうことかというと、富士山の左側の裾と右側の裾で斜面の角度が違いすぎるから、宝永山の裾をもっと緩やかにしたいということです。言われてみれば確かにその通りです…。宝永山を作る位置で、途中から$f\circ h^{\prime\prime}\left(x\right)<0$とできれば、他の部分ともっと自然な形で繋がりそうですね。ここはもう少し考えてみましょう。

４．もうちょっとこだわってみる

今の問題では、$h(x)$に登場する$e$の指数部分は、次のように二次関数と呼ばれる形をしています。

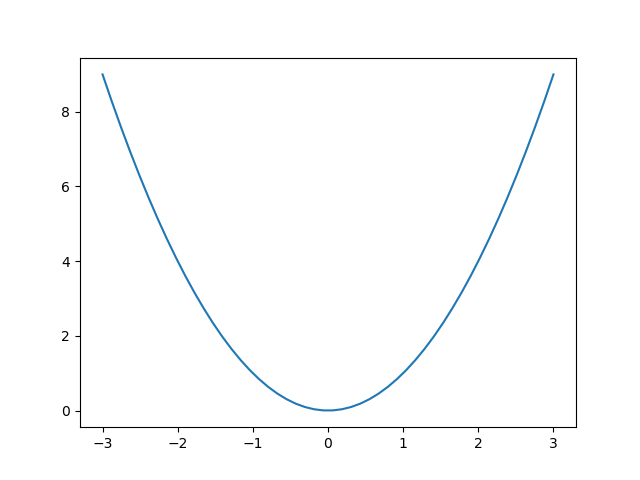
このグラフに「変曲点」を持たせるため、次のような三次関数と呼ばれる形を考えてみましょう。

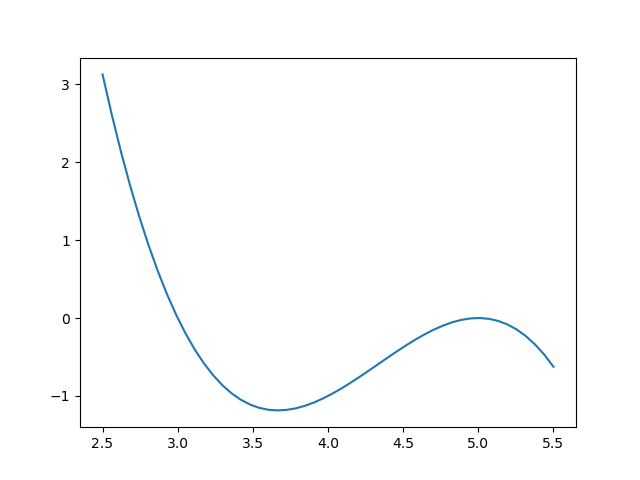
注目すべきはこの部分です。

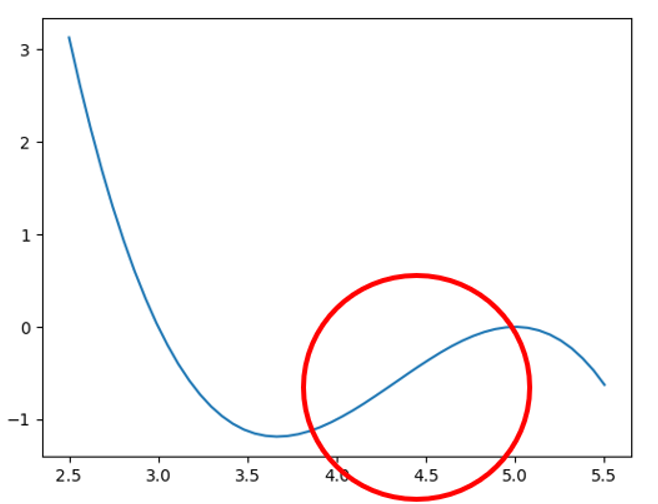
途中までは二次関数と同じ谷の形を作っていますが、だんだんと山の形を作る傾向に変わっています。この傾向が変わる瞬間が変曲点です。このような関数を先ほどの$h(x)$に導入してみようと思います。具体的には、$-(x-3)(x-5)^2$という三次関数を使います。これで$h(x)$は$3 < x <5$の範囲で先ほどの条件を満たし、変曲点も$x=4.3$付近に来るというわけです。

さて、それでは改めて、宝永山を再現した問題がこちらです。

関数$f(x)$,$g(x)$,$h(x)$を

$$\begin{align*} f(x) &= \left\{ \begin{array}{11} x^4-x^2+6 & (|x| \leq 1)\\ \frac{12}{|x|+1} & (|x| > 1) \end{array} \right.\\ g(x)&=\frac{1}{2}\cos (2\pi x)+\frac{7}{2} \hspace{1.0em}(|x|\leq 2)\\ h(x) &= \left\{ \begin{array}{ll} xe^{-\frac{1}{3}(x-3)(x-5)^2} & (3 \leq x \leq 5)\\ x & (x < 3, 5 < x) \end{array} \right.\\ \end{align*}$$

で定義する。このとき、次の問いに答えよ。

(1) $f \circ h(x)$,$g(x)$の増減を調べ、2曲線$C_1:y=f \circ h(x)$,$C_2:y=g(x)$のグラフの概形を同じ座標平面上にかけ。

この問題に従って描いたグラフが、こちらになります。

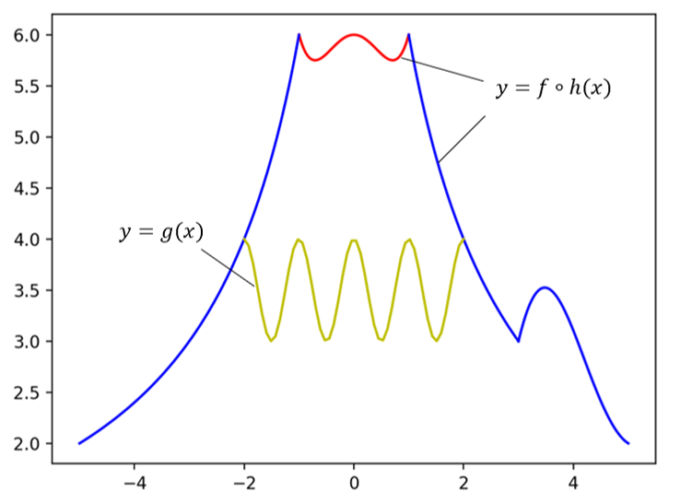
今度こそ、宝永山を再現することができました！

５．まとめ

いかがでしたでしょうか。前回の静岡大学の入試問題をアレンジして、宝永山を再現した問題にしてみました。こだわった場所は何点かありましたが、実は他にも考えれば考えるほど「こんな関数にしたい！」という思いが出てきてしまいます。たとえば、可能であれば宝永山とほかの部分はもっと滑らかにつなげたい（つまり微分可能にしたい）ものです。それから、今回は変曲点を三次関数で再現していますが、この三次関数は指数関数に合成したり$x$をかけたりとたくさん改造しているので、実は今回のような綺麗な位置に変曲点が出てきたはたまたまだった…という可能性もあるのです。そんな背景もあるので、いつかはこういった疑問をすべて解決した富士山を書いてみたいですね。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

<文/伊藤智也>

ブラタモリ (2) 富士山 東京駅 真田丸スペシャル