グラフとは【算数からやさしく解説】
公開日
2022年6月2日
更新日
2025年9月18日

↓↓↓動画で見たい方はこちら↓↓↓
この記事の主な内容
グラフとは
数学(算数)におけるグラフとは、関数を目で見て分かるように(座標)平面などに書いたもののことです。例えば、比例のグラフは直線、反比例や二次関数と呼ばれるものは曲線(双曲線や放物線)になります。
(実は数学には同じ「グラフ」という言葉を使ったものとして、グラフ理論と呼ばれるものがありますが、今回の関数に関するグラフとは特に関係はありません。「グラフ」などで調べるときには注意してください。)
今回はこのグラフについて例を交えながら解説していきたいと思います。
グラフの考え方
ある関数のグラフとは、\(xy\)座標に\(x,y\)がそれぞれその関数の式を満たすような点を集めたものです。つまり、グラフとはあくまでも無数の点が集まって直線や曲線になったものなのです。このことは例を考えることで非常にわかりやすくなります。
まずは例として\(y=-2x\)を考えてみましょう。まずは\(x\)に様々な値を代入してそれぞれの値に応じて\((x,y)\)を座標平面に書いていきます。
実際に\((x,y)\)として\((0,0)(1,-2)(-2,4)(-\frac{1}{2},1)(3,-6)(\frac{3}{2},-3)\)などは\(y=-2x\)を満たしていることがわかり、点を打っていくと下図のようになります。
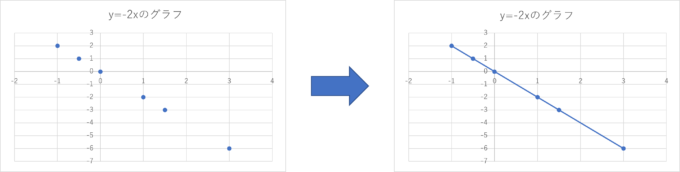
このような具合でさらに点を打っていくと、下図のようにだんだんと直線になっていることがわかると思います。
グラフの例
次に\(y=x^2\)のグラフについて考えてみましょう。もしこの関数についてよく知らなくも\(x\)に値を代入して、どのような点\((x,y)\)がこの関数を満たすのか、またその点を打つとどのような図形になるかを試してみると下図のようになります。
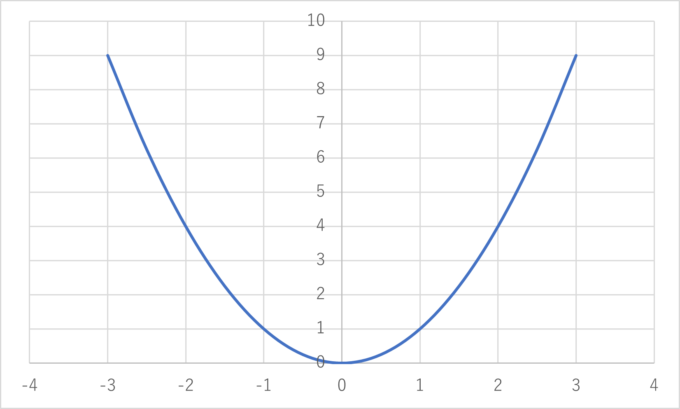
このように、関数の式の形さえわかればある程度その関数のグラフの形を推測することができます。
グラフからわかること
これまで見てきたように、それぞれの関数に対してそれに対応するグラフ(図形)があることがわかります。また、このようなグラフを考えることで\(y=-2x\)は\(x\)が増えれば増えるほど\(y\)が減ること、\(y=x^2\)は\(x\)が\(0\)(原点)から離れれば離れるほど\(y\)が大きくなることがわかります。このように、グラフを書くことで大雑把にその関数について知ることができます。
グラフのメリット
グラフは、普段は式の形でしか見ることのできない関数を、私たちの見ることのできるような図形として認識することができる点で非常に有用です。このように、関数を図形としてみることによって、それまで知られていた関数の性質をより深く理解できたり、別の見方をすることで新しい発見がされたりしてきました。また、図形(幾何)の問題を(直線や円などの)関数によって統一的に扱うことができるようになり、たとえ計算の手間が多かったとしても補助線などを用いずに機械的に解くことができるようになります。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/尾崎>