↓↓↓動画で見たい方はこちら↓↓↓

座標（平面）とは

座標（平面）とは、平面上の点の場所を座標とよばれる2つの数の組（座標）によって表せるような平面のことです。
今回はなぜ２つの座標を使うのかと座標の考え方（イメージ）について解説していきたいと思います。

なぜ2つの数を使うのか

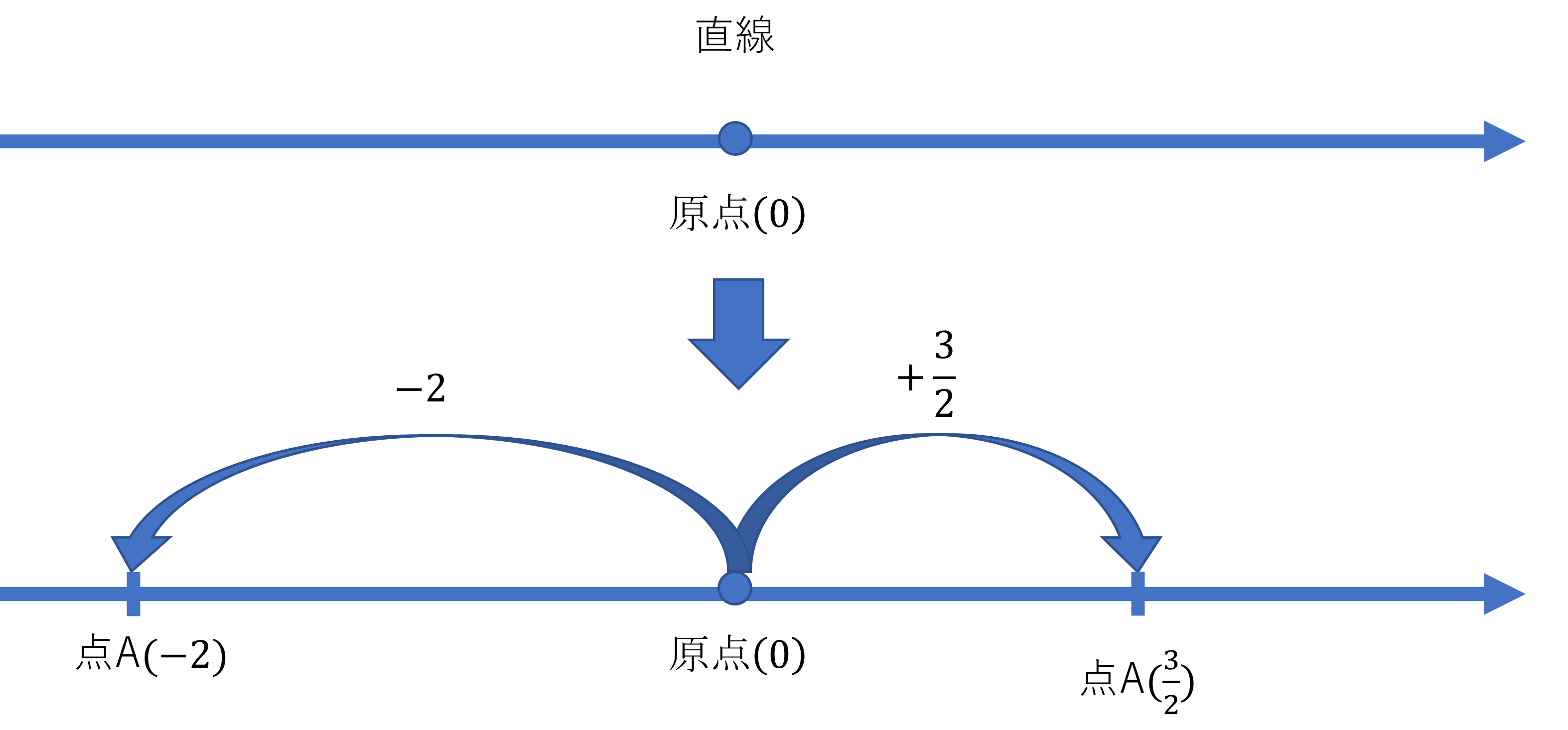
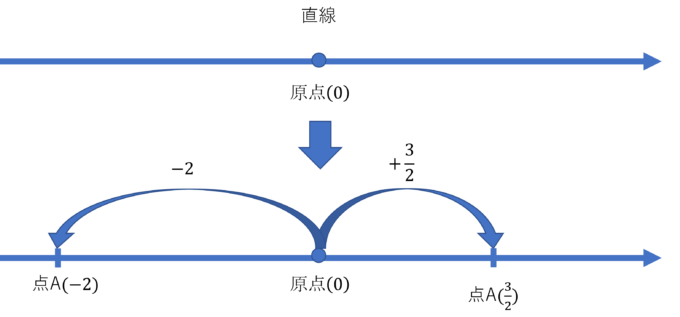
平面について考える前に、まずは直線について考えてみたいと思います。平面の点を決めるのに2つの数の組が必要なのに対して直線では1つの数で点の位置を知ることができます。
直線に原点と呼ばれる0となる点を決め、その原点からaだけ移動したところをaとしていました。このときのポイントは、数を1つ決めれば直線上の点が1つに決まるということです。そしてこの直線を数直線と言っていました。

このような話を平面でも同じようにしていきたいと思います。ある平面上の点Aを数字で表すことを考えてみましょう。まずは平面での原点の位置を決めます。実は、この原点に対して点Aを1つの数だけでは表すことができません。
例えば、数直線と同じように原点からどれだけ移動したかでその点の位置を表そうとしても、その点を通る円上の点を同じ点とみなしてしまっているので点の位置が定まらないです。

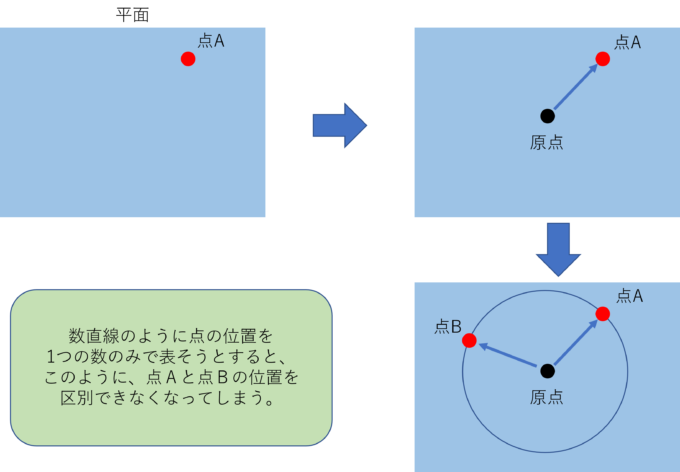
このようなことから平面の点は、2つの数を用いなければその位置を表すことができないのです。

座標のイメージ

座標とは地図のようなものです。例えば、世界地図を見てみると緯度（いど）と経度（けいど）と呼ばれる縦と横の線があると思います。これがあることによって世界中のあらゆる場所をこの緯度と経度の組で表すことができます。地図と座標の違いは地図には限られた範囲の平面しかないですが、座標には無限に広がる平面があることです。

座標平面のメリット・デメリット

実は、平面に座標のように基準（原点や数直線）を用いることで、初めて距離などの私たちが当たり前に使っているもの数学でも使えるようになります。このことを応用すれば地球のような球体やドーナツ型などの立体などにも“座標”を考えることができます。
しかし一方で、今回例に挙げた世界地図は、元々球だった地球を無理やり平らなものにしていて実際の縮尺とはずれてしまっています。このように、面積や長さと言ったものが元のものと合わなくなってしまう場合もあります。

座標の考え方の活用例

これまでで座標についていくつか話してきたように、直線では1つの数で、平面では２つの数を使って点の位置を表すことができます。それでは私たちが生活の中で認識している横幅、奥行き、高さがあるような空間では何個の数を使えば点（もの）の位置を表すことができるでしょうか。

答えは\(３\)つです。横幅、奥行き、高さと説明したように、この3つについての値がわかれば空間の中の点の位置を知ることができます。
これまでと同じような考えたとえを使うことで、私たちが認識できないような“世界”について知ることができ、現代ではそのようなものがさまざまなところで利用されています。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

グラフとは【算数からやさしく解説】

<文/尾崎>