↓↓↓動画で見たい方はこちら↓↓↓

関数とは

関数とはざっくり言うと、入力した値（数）に対してある規則でもう一つの値を出力するルール（仕組み）のことです。関数と聞くと一次関数や二次関数などが思い浮かぶかもしれませんが、他にも小学校で学ぶ比例や反比例も関数です。
前回までに、関数になるものとならないものの例を通して関数とはどういったものかについて解説してきました。今回からは、\(y=2x\)や\(y=x^2\)などの実際に数学（算数）で使われている文字を使って関数を表すことついて説明していきたいと思います。

どんなものが関数か

少し前回までの内容を復習してみると、関数とは
1.ある値が入力される
2.その値がある規則によって変えられる
3.1つの（1通りの）値が出力される
といった流れがある仕組みのことを関数ということがわかりました。
関数としてみなせるものはタクシーのメーターや自動販売機などがありました。

ｘやｙを使って関数を表すには

実際に関数が使われるのは入力と出力が数であるものです。例えば、これまでの例のタクシーのメーターは数（走った距離）を入力して、数（運賃）を出力していました。一方で、自動販売機では入力は数（お金）でも、出力には数ではない飲み物が使われていました。
それでは、「走った距離（入力）を2倍して運賃を出力する」タクシーのメーターを文字x,yを使って、実際に使われる関数の形を考えていきます。
このx,yはさまざまな数を代入（その文字をある数として置き換えること）して変えること出来るので変数と呼ばれます。
\(x\)を入力する数（走った距離）、\(y\)を出力される数（運賃）として考えると、このタクシーのメーターの規則は\(y=2x\)とわかります。図にすると下図のようになります。

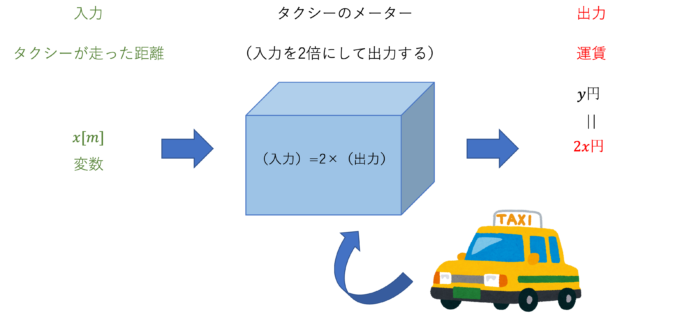
こうすることで例えば、もし別の関数とみなせる仕組みを持つものが変数を使うことで\(y＝2x\)と表せると分かれば、全く違うものに見えても本質的には同じことをしていることがわかったり、違うタクシーのメーターとどちらの方がお得なのかを数値として知ることができたりするようになります。

関数を文字で表す例

もう一つ例を見てみましょう。\(0\)より大きい数を入力すると、それを１辺の長さとする正方形の面積を出力するというものを考えてみます。これは上の1〜3を全て満たしているので関数になっています。
入力される数を\(x\)、出力される数を\(y\)とすると、1辺の長さが\(x\)の正方形の面積は\(x^2\)なのでこの関数は式で表すと\(y＝x^2\)(\(x\)は0以上)だとわかります。
これまでの例を通して気づいた方もいるかもしれませんが、本来は関数を変数で表すときの文字は\(x\)や\(y\)でなくても\(a\)や\(t\)、\(□\)などでもいいのですが、数学の慣習で\(x\)と\(y\)が広く用いられています。

関数の活用例

これまでいろいろな例を通して関数について解説してきましたが、主に入力や出力が数（実数や複素数（ふくそすう））に関するものであるときに関数といい、より広く入力や出力が、数に限らず文字や動物などになるものを写像（しゃぞう）ということが多いです。自動販売機の例はどちらかというと写像の考え方に近いです。
写像というのは基本的に高校まででは習わないですが、より抽象的になったことで関数以上にさまざまなところで顔を出します。

●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら

関数とはならないもの【算数からやさしく解説】

<文/尾崎>