こんにちは。和からの西原です。
社会人になると算数・数学が苦手でもどこから学び直したらよいかわからない・・・といったご相談を解決するためにスタートしましたが、今回は、「引き算の性質と計算の工夫」について記載します。
前回の内容「引き算の繰り下がりを楽にする方法」では、引き算の考え方を記載しているので、ぜひこちらもご覧ください。

引き算の繰り下がりを楽にする方法-考えたくなる算数⑥-

１．引き算の「差は変わらない」性質を利用した計算の工夫

11 – 4 の計算を考える際、長さ11cmと4cmの紐を思い浮かべてみてください。
次は、それぞれを1cmずつ短くした10cmと3cmの紐を思い浮かべてみてください。
引き算の性質で解説した「求差」で考えると良いと思います。
11 – 4 = 7
10 – 3 = 7 差は同じ7になります。
この性質を、引き算の繰り下がりに利用してみたいと思います。

計算の工夫①

41 – 18 の計算をしていきます。
もとの数(引かれる数)を、近くの区切りの良い数に減らします。
【STEP1】41を1減らして、40にします。
【STEP2】18も1減らして、17にします。
【STEP3】40 – 17を計算すると、23になります。
差は変わりません。つまり、 41 – 18 = 40 – 17 = 23となります。

計算の工夫②

同じく、41 – 18 の計算をしていきます。
今度は、引く数を区切りの良い数に合わせたいと思います。
【STEP1】18を2増やして、20にします。
【STEP2】41も2増やして、43にします。
【STEP3】43 – 20を計算すると、23になります。
差は変わりません。つまり、41 – 18 = 43 – 20 = 23となります。

数を大きくしてみよう

計算する数を大きくすると、効果がもっと感じられると思います。
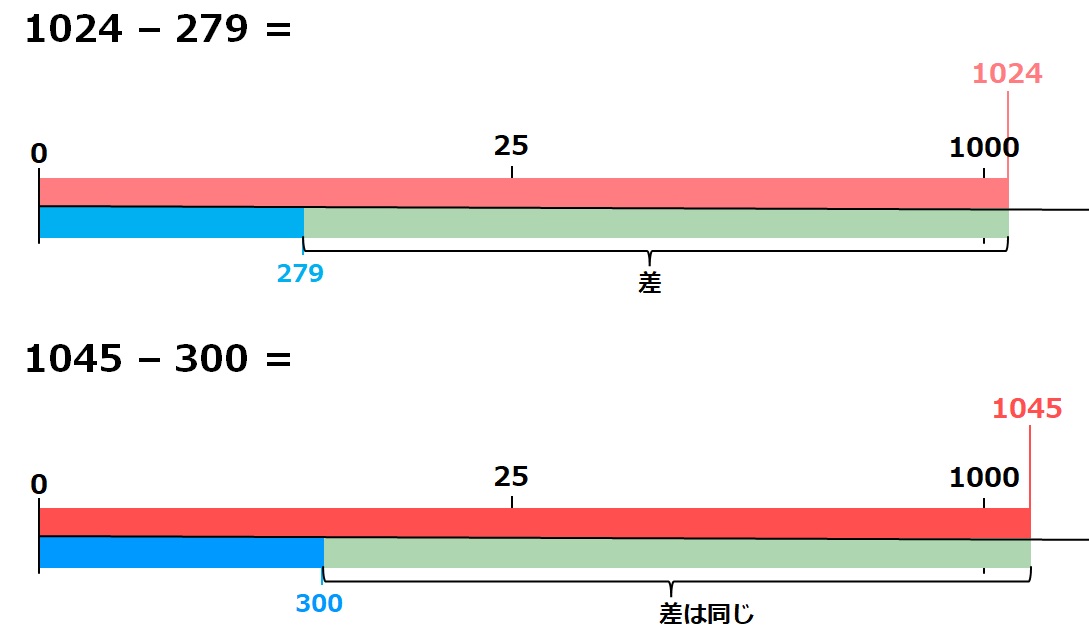
1024 – 279の計算は暗算しようとすると、難しく感じます。
279を区切りの良い『300』にします。（21増やします）
1024も21増やすと、計算は1045 – 300 = 745となり、暗算が楽になりました。
つまり、1024 – 279 = 745となります。

２．引き算を足し算で考える

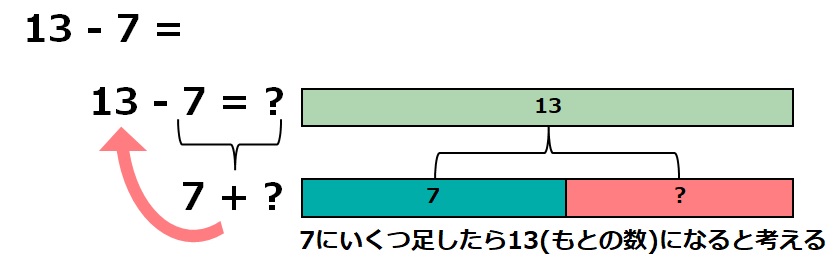
13 – 7の答えを『?』とした場合、
13 – 7 = 『?』 と表すことができます。
引く数7とその答え『?』を足すともとの数になります。
この性質を利用すると、
【STEP0】「7にいくつ足すともとの13になる？」と考える
【STEP1】7に『3』を足して、10にします。
【STEP2】10に『3』を足して、13にします。
【STEP3】3 + 3 = 6となり、13 – 7 = 6と同じになります。
つまり、13 – 7 = 6となります。

練習問題

計算を行う前に、数を観察すると、「どの計算方法が楽になりそうか」と考えるヒントをくれます。
計算は楽な方が、「早い。間違えにくい。」と思いますので、いくつか問題を準備しました。良かったらチャレンジしてみてください。
わたしが楽だなと感じる方法を記載していきます。
①91 – 37 =
②331 – 150 =
③10000 – 2199 =
④7801 – 7681 =

問題の答えと、パッと思い浮かんだ工夫した計算方法を記載します。
【答え①】54
《工夫と使った式》91 – 40 + 3 、90 – 36、94 – 40
【答え②】181
《工夫と使った式》331 – 200 + 50 、381 – 200
【答え③】7801
《工夫と使った式》10000 – 2200 + 1、10001 – 2200
【答え④】120
《工夫と使った式》7681 + ? = 7801、201 – 81

今回は、「引き算の性質と計算の工夫」についてご紹介させていただきました。
次回は「頭の中で足し算や引き算を利用する場面について」日常生活や仕事などを題材に
紹介します。
(文/西原)

「和からの個別指導」では、どんなに苦手な方でも自分のペースで学ぶことができます。
算数から苦手意識を克服したい方など、ご興味があれば一度無料カウンセリングでご相談ください！

無料相談お申し込み