比例とは【算数からやさしく解説】
公開日
2022年4月12日
更新日
2025年9月17日

↓↓↓動画で見たい方はこちら↓↓↓
この記事の主な内容
比例とは
比例とは一方が何倍かされると、もう一方も同じように何倍かになる関係のことです。
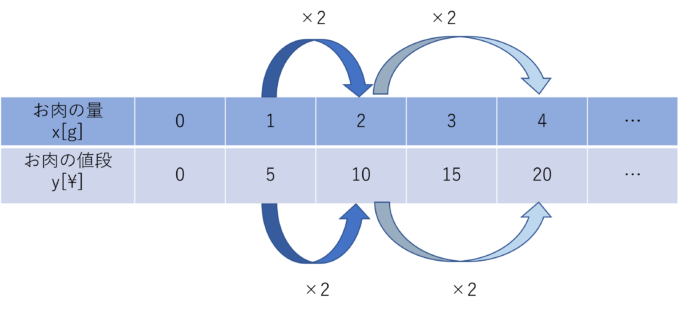
例えば、お肉の量と値段は、買うお肉の量を2倍,3倍,…にしていくと払う値段も2倍3倍,…になっていくので比例の関係になっています。
比例の式
先ほどのお肉の量をx[g]、値段をy[¥]とすると、xとyの関係は、ある数aを使って
\begin{align*}
y=ax
\end{align*}
と書けます。ここでのaは、常にyがxのa倍になっているということで比例定数と呼ばれます。今回のお肉と値段の例では比例定数aやxは正の数でないといけませんが、基本的に比例と言われたらxやaは実数の値をとります。

比例定数aを5としたy=5xを表にすると下図のようになります。
比例のグラフ
次は比例のグラフについて説明したいと思いますが、その前に関数のグラフについて復習したいと思います。
数学ではy=axのような式(関数)を横軸(x軸)と縦軸(y軸)を書いた座標平面に、その関数の式が成り立つような点を打つことで図形として表示したものをグラフと言います。
(実は数学にはいくつかの点とそれらを結ぶ線分のことなど、別の意味でグラフと呼ばれるものもあります。)
例えばy=5xであれば ,(x,y)(xとyの組)が\((1,5),(2,10)(\frac{1}{2},\frac{5}{2})\)など無数の点を座標平面に打つことができます。この無数の点をすべてつなげたものがグラフであり、特にy=5xは比例の式だったのでこのグラフを比例のグラフと呼んだりします。
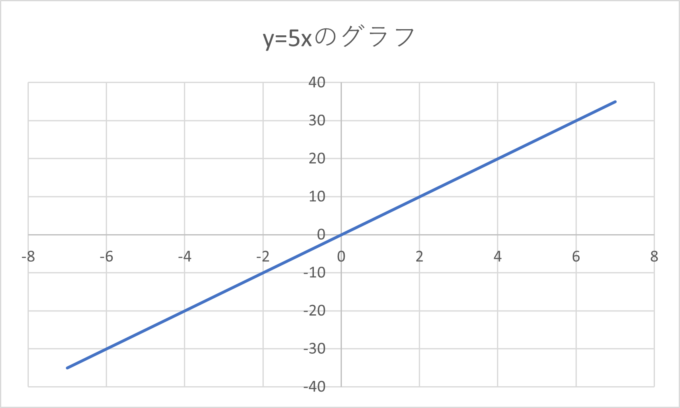
このグラフを見て分かるように、比例のグラフは0=5×0なので原点(x軸とy軸の交点)を必ず通り、なおかつ直線になる特徴があります。
また、比例定数aは大きくなればなるほど直線の“傾き”が右肩上がりになり、小さくすればするほど右肩下がりになります。このようなことから、比例定数を傾きということがあります。
比例のメリット
比例は生活でも広く応用できる数学の考え方の基礎であり、特に一次関数の理解にもつながるので非常に重要です。
比例の活用例
比例の関係は数学だけではなく物理の世界でよく見られます。なので、私たちの生活のいたるところで使われ支えている概念でもあります。
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/尾崎>
















