線形代数
公開日
2021年4月22日
更新日
2023年1月6日
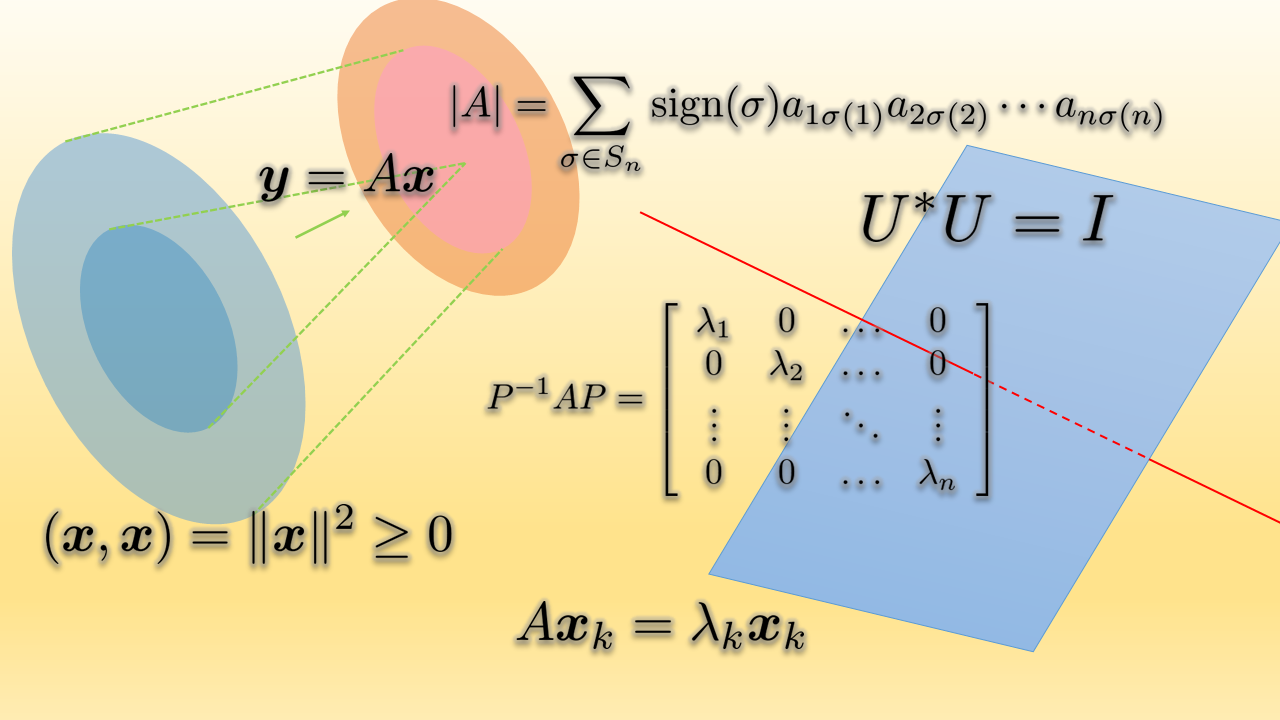
線形代数は現代数学の基礎的な役割を果たす数学の分野であり、現代数学に限らず多くの理系分野で道具として用いられています。特に最近では、統計学や機械学習といった数学の応用分野において、その手法やアルゴリズムを記述するために必要という理由から、線形代数を学びたいというお客様が増えています。
線形代数は一言でいうと「線形」という性質を持つ集合や写像を扱う学問です。線形性を持つ数学的対象は多く知られていますが、線形性を持たない対象も線形化を行うことで近似的に線形性を持たせることができます。
こういった理由から線形代数は様々な分野で用いられており、例えば工学や物理において応用的な問題を解くために微分方程式これを解くために線形代数の知識が必要となります。
受講内容
線形代数の主役はベクトルと行列です。まずベクトルと行列について基本的な演算を学んでいきます。そして数ベクトル空間という基本的なベクトル空間にて線形写像や行列式の意味について理解を深めます。
数ベクトル空間とその上の線形写像は中学校以来習ってきた連立方程式の一般化となっており、連立方程式を見通しよく解くための手法について学びます。
その後、数ベクトル空間に限らない一般のベクトル空間を定義し、様々なベクトル空間の例を見ます。そしてどんなベクトル空間も基底を定めることで数ベクトル空間の理論で記述できることを確認します。
また、ベクトル空間に内積を考え、ベクトルの長さやベクトル間の距離を考えることができる計量ベクトル空間についても学びます。
最後に応用上最も重要な行列の対角化について学びます。対角化の意味や、なぜ対角化できると嬉しいのか、といった本質について解説します。
※内容はお客様のご要望等によって変更することがあります。
受講対象
・大学のレポート問題、試験問題が解けない方
・線形代数の知識がなく応用分野(統計、機械学習、物理学等)の学習が進まない方
・線形代数を数学的に楽しみたい方
必要な数学知識
モデルプラン
担当講師
※日程により一部講師が変わる事があります。