積分の歴史～ルベーグ積分までの道のり～

おすすめイベント・ゼミ

公開日

2020年9月4日

更新日

2020年9月4日

※本記事はロマ数トレラン「ルベーグ積分入門セミナー」の講師である山本拓人先生によるルベーグ積分の入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

ロマ数トレラン「ルベーグ積分入門セミナー」の詳細、お申し込みはこちらのページよりお願いいたします。⇒http://romanticmathnight.org/1480

この記事の主な内容

はじめに

高校数学で初めて「積分」に出会い，「こんな曲がった境界をもつ図形も面積が求められるのか！」と衝撃を受けた人は多いかもしれません．

大学の微分積分学の授業では，高校数学の積分はリーマン積分という厳密に定義された積分が元になっていることを学びます．しかし，リーマン積分の考え方はシンプルですが，数学的には少々扱いづらいという欠点があります．

1900 年頃の数学者であるアンリ・ルベーグはリーマン積分とは異なる考え方の積分を考え，現在ではこの積分はルベーグ積分とよばれています．

ルベーグ積分はリーマン積分の欠点を改善することができており，これによりリーマン積分では計算できなかった積分もルベーグ積分では積分できるようになるという恩恵も生まれました．

この記事では，積分がどこから起こり，どのように発展し，ルベーグ積分が考えられるようになったかの道のりを説明します．

積分の原型

積分の原型が生まれたのは紀元前2000 年の古代エジプトだったと言われます．

赤道がまともに通るアフリカ大陸は暑い印象がありますが，最高峰の標高が5000m を超えるルウェンゾリ山地には雪が降り，春になると雪解け水がナイル川に流れ込みます．

これによりナイル川が氾濫し，上流から流れてきた栄養豊富な土がその年の農作の糧となります．これが「エジプトはナイルの賜物」という言葉の背景ですね．

ここで１つ問題がありました．ナイル川が氾濫すると地形を変えてしまうので，再び測量して土地を分割し直さなければなりません．

ここで考えられた測量術は，三角形で少しずつ土地を覆い，三角形の面積の和で土地の面積を求める方法で，取り尽くし法とよばれます．

三角形の面積は当時もよく知られていましたから，これで土地のおおよその面積が分かることになります．

なお，このような「土地(geo) を測る(metry) こと」は「幾何学」を意味する“geometry” の語源にもなっています．また，この測量術では三角形で何回埋め尽くそうとしても完全に埋め尽くすことはできませんが，実用上はだいたいの土地の面積が求まれば十分だったからでしょうか．それから長らくの間，曲がった境界をもつ領域の面積を厳密に考える理論はあまり考えられなかったようです．

積分の幕開け

1600 年代に入るとヨーロッパでは数学が全体的に大きく発展を見せ始めます．

ルネ・デカルト(René Descartes) は2 つの数を「縦」と「横」の2 方向で図示できることを思い付き，これにより関数$f$に対して$y=f(x)$を$xy$平面上に曲線(グラフ)として図示できるようになります．また，逆に様々な曲線(グラフ)が$x$と$y$の方程式によって理解されるようになり，領域の面積を積分で表す考え方が生まれます

例えば，$y=x^2$は$xy$平面上に以下のように図示することができ，現代では灰色の部分の面積を
\[
\int_{-1}^1x^2dx
\]
と表します．

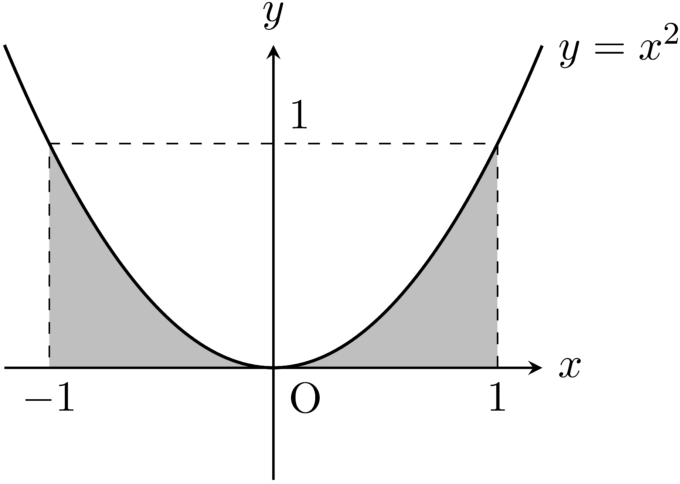
大雑把にいえば，関数$f(x)$のグラフ$y = f(x)$と$x$軸で囲まれた部分の$a\leq x\leq b$の部分の(符号付き) 面積を

\[
\int_{a}^bf(x)dx
\]

と表すわけですね．この$\displaystyle \int$をインテグラル(integral) と読み，$\displaystyle \int$による計算を積分とよびます．

たとえば「デカルトの正葉線」と呼ばれる
\[
x^3 + y^3 = axy\qquad (a > 0)
\]
で表される$xy$平面上のグラフは以下のようになりますが，この曲線で囲まれる部分の面積も積分の考え方を使えば求めることができます．

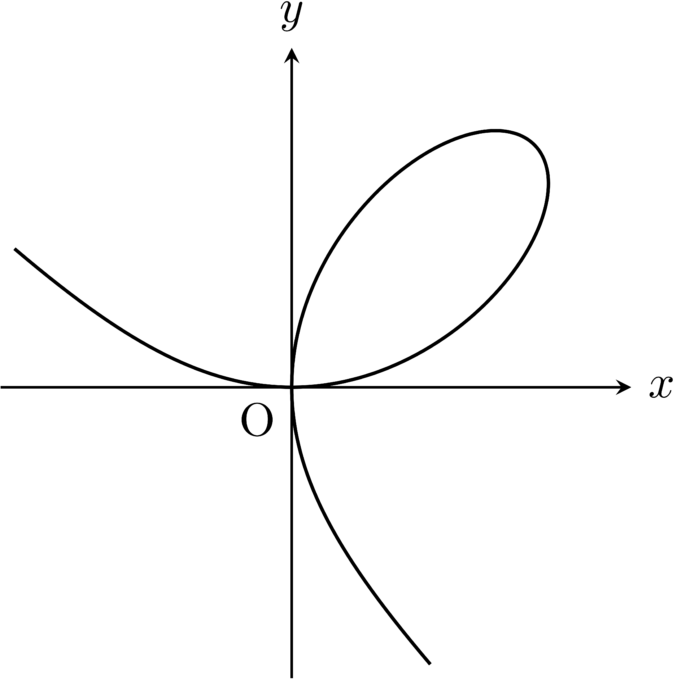
しかし，当時は積分を計算する一般的な方法が知られておらず，1 つ1 つの積分の計算は様々な工夫のもとに行われていました．

例えば，いま図示したデカルトの正葉線で囲まれる部分の面積の古典的な求積法については「古典的難問に学ぶ微分積分」(高瀬正仁著，共立出版) で紹介されていますので，気になる方はこちらの書籍を参照にしてください．大学で学ぶ微分積分学の知識は本書の中で説明されているため，高校数学の微分積分が理解できていれば読める内容となっています．数学好きの高校生～大学1,2年生にオススメしたい良い本です．

積分と微分

中世のヨーロッパで積分を計算する一般的な方法が知られていなかったのは，まだ微分の考え方が確立されていなかったのが大きな理由です．

微分はアイザック・ニュートン(Isaac Neton) とゴッドフリート・ライプニッツ(Gottfried Leibniz) がそれぞれ独立に考え出したものとされています．

この微分の功績を巡って2 人は争うことになり，とこの話はとても人間くさくて好きなのですが長くなるのでここでは割愛します．気になる方は是非とも調べてみてください．

微分が考え出されると「微分と積分はどうやら繋がっていて，『性質のよい関数』に対しては微分と積分は逆の関係になっているらしい」ということが分かってきます．このことは今では微分積分学の基本定理とよばれています．

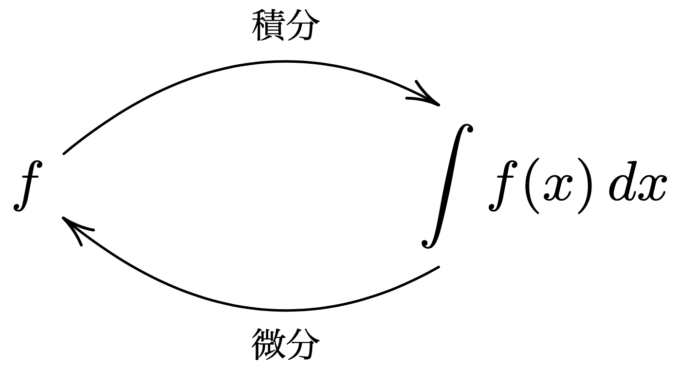
高校数学で「積分は微分の逆演算(=微分してもとに戻る関数を求めるのが積分)」と学ぶのは，この「微分積分学の基本定理」が背景にあるからなのです．このように高校数学では「微分」→「積分」の順番で学ぶものの，歴史的には微分よりもずっと先に積分が考えられていたのは，少し驚きがあるかも知れませんね．

これにより積分の一般的な計算方法が考えられ，様々な数学者によって積分は微分と併せて大きく発展していくことになります．なお，微分積分学の基本定理について知りたい方は，私の運営するブログの記事が参考になると思うので，最後の参考文献から読んでみてください．

なお，現代の微分の記号$\displaystyle \frac{dy}{dx}$を考えたのはライプニッツです．この記法により微分と積分の関係を見事に表現することができ，この意味でライプニッツの記法は微分積分学の発展に大きく貢献したといえますね．

リーマン積分

その後，数学界全体で数学をより厳密に整備し直すべきだという風潮が広まります．もちろん，この風潮は積分に対しても例外ではありませんでした．

1800 年代になると，ベルンハルト・リーマン(Bernhard Riemann) は積分の厳密な定義を与えました．

リーマンは$\displaystyle \int_0^1f(x)dx$を計算するには「$xy$平面上の$y=f(x)$のグラフと$x$軸で囲まれる$0 \leq x \leq 1$の領域を縦長にスライスし，長方形によって近似すればよい」と考えました(厳密にはもう少し複雑です)．

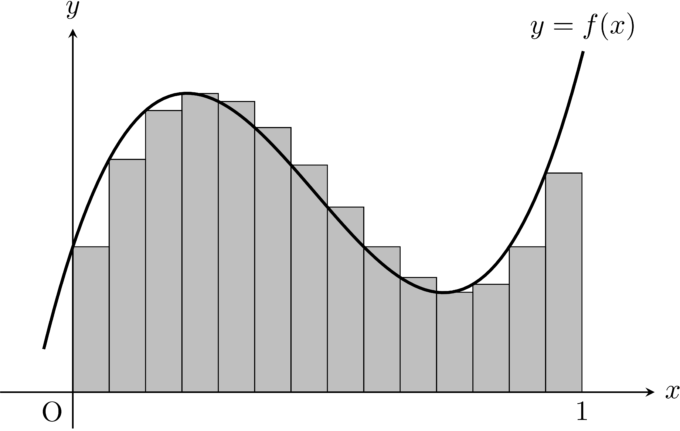
この考え方による積分をリーマン積分といいます．

もちろん，この図のように「荒いスライス」では長方形で近似した面積(灰色の部分) と，もともと考えていた$\displaystyle \int_0^1f(x)dx$に差があります．しかし，このスライスの幅をもっと細かくすると，長方形で近似した面積はより$\displaystyle \int_0^1f(x)dx$に近付くことが見てとれます．

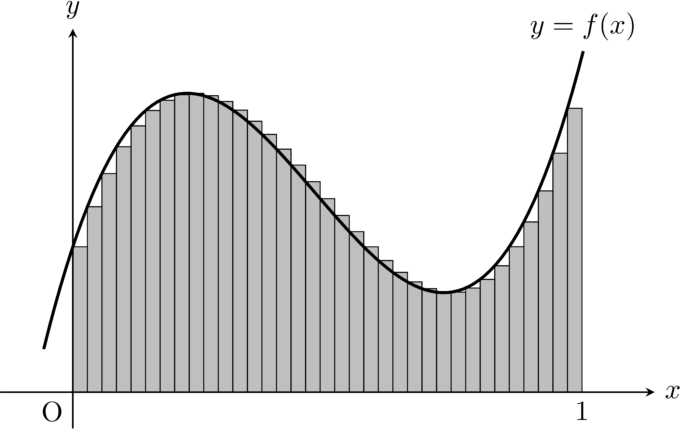
このように，「スライスの幅(の最大) を$0$に近付ける」という極限をとって長方形近似による面積が収束するとき，この極限を$\displaystyle \int_0^1f(x)dx$と定義しようという考え方がリーマン積分のイメージです．

しかし，実はリーマン積分では「長方形近似の高さ」を決める段階で問題が生じて，リーマン積分を考えられない関数もあります．

このことについて詳しい説明は省略しますが，少し例を考えてみましょう．

\[
f(x)=\begin{cases}1&(\text{$x$は有理数})\\0&(\text{$x$は無理数})\end{cases}
\]

という関数$f$は「ディリクレ(Dirichlet) 関数」という名前がついています．ディリクレ関数$f$は\begin{align*}
f\left(4\right)&=f\left(\frac{1}{2}\right)=f\left(\frac{4}{3}\right)=1,\\
f\left(-\sqrt{2}\right)&=f\left(\pi\right)=f\left(\log_{2}{5}\right)=0
\end{align*}のように，有理数を代入すると$1$を返し，無理数を代入すると$0$を返すような関数です．「え？こんなのが関数？」と思われるかも知れませんが，$x$を決めると$1$つだけ値を返してくれるものを関数というので，これもれっきとした関数です．

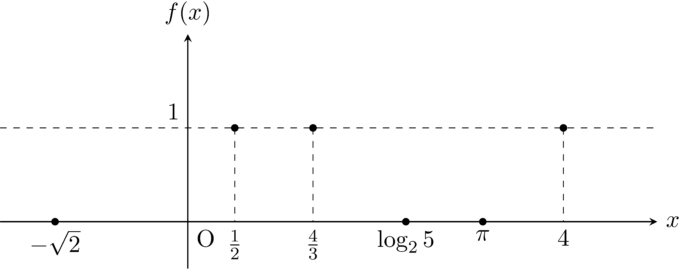
無理数と有理数は極めて細かく入り組んでいることが知られており，ディリクレ関数$y=f(x)$のグラフは「$0$と$1$を非常に細かくぴょんぴょんと飛び移るグラフ」になります．すると，どんなに細かくスライスしたとしても，どのスライスにも
・高さ$0$の点
・高さ$1$の点
が含まれてきてしまうため，スライスの長方形の高さを$0$にすればいいのか$1$にすればいいのか困ってしまいます．こんな「ゲテモノ」を持ってくると，リーマン積分では「食べる」ことができないのです．

ルベーグ積分

とはいえ，「ディリクレ関数を積分しても意味なんかないんじゃない？」という意見もあるかも知れません．

確かに，ディリクレ関数$f$に対して，「$xy$平面上の$y = f(x)$ のグラフと$x$軸で囲まれた領域の面積」というのもよく分かりませんから，本来は面積を求めるところから出発した積分が考えられないのは自然にも思えます．

しかし，抽象化こそ数学の本領で，抽象化によってこれまで見えなかったものが見えるようになることはよくあります．

1900 年頃，アンリ・ルベーグ(Henri Lebesgue) は積分の新しい定義を考えました．リーマン積分では「縦に切る」のに対して，ルベーグの新しい積分の考え方では「横に切る」ことで積分を定義しました．

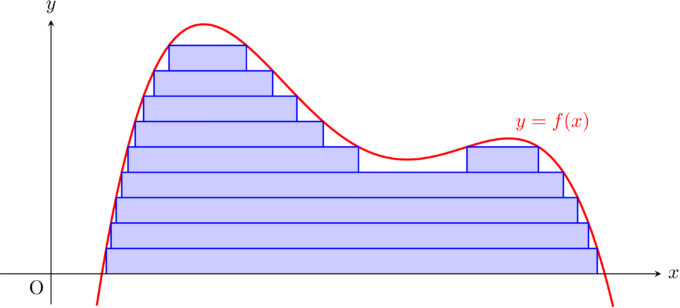
「縦に切ろうが横に切ろうが同じじゃない？」

いえいえ，実はこの切り方の違いが大きな違いを生むのです．

結果を言えば，このルベーグの「横に切る」方法を用いると，ディリクレ関数$f$ の$0 \leq x \leq 1$での積分は
\begin{align*}
\int_0^1f(x)dx&=(0\leq x \leq 1 \text{での有理数の長さ})\times 1 \\
& \qquad +(0\leq x \leq 1 \text{での無理数の長さ})\times 0\\\\
&=(0\leq x \leq 1 \text{での有理数の長さ})
\end{align*}
と考えることができるのです．

「有理数の長さ」と「無理数の長さ」というのものは本来はきちんと定義しないといけないのですが，ここでは結果だけを使いましょう．

実は「有理数の長さ」は「無理数の長さ」と比べると無視できるほどに圧倒的に小さいことが知られており，「有理数の長さ」は$0$に等しくなります．したがって，
\[
\int_0^1f(x)dx=0
\]
と計算できることになるのです．なんと「ゲテモノ」を食べることができてしまいました！

なお，「有理数は無理数に比べて少ない」ということだけなら，「カントール(Cantor) の対角線論法」というものによって証明することができます．「対角線論法」という名前を聞いたことがある人は少なくないかも知れませんね．

この「対角線論法」については私のブログでも記事にしたことがあるので，最後の参考文献から参照してみてください．