数理統計学事始-平均値と中央値をさまざまな視点でみる-

統計・機械学習トピック

公開日

2020年9月6日

更新日

2020年9月6日

こんにちは。和からの数学講師の岡本です。今日は平均値と中央値についてお話をします。数値のデータがいくつかあるとき、特徴を捉えるためにこうした「統計量」と言われる指標を計算することがあります。今日は「平均値」「中央値」について、一般的なとらえ方から、あまり知られていない特徴までをご紹介していきます。

この記事の主な内容

１．平均値とは

\(n\)個のデータ\(x_1, x_2, \ldots, x_n\)があるとします。平均値とはその名の通り、「平らに均（なら）す値」です。求め方は皆さんご存じの通り、
\begin{align*}
\bar{x}=\frac{1}{n}(x_1+x_2+\cdots +x_n)
\end{align*}
で得られます。つまり、データを全て足し合わせて、データの個数\(n\)で割ります。この時点で１つポイントとなるのは、「平均値はデータ全てを使って表されている」ということです。つまり、平均値はデータ全ての情報を利用しています。

上記の説明が少し難しく感じる方や、統計を始めて学ぶ、興味があるとういう方向けに数式を用いない統計学の無料セミナーを行っています。

文系のための「統計超入門セミナー」-目で見てわかるビジネス統計学-

こちらも超オススメですので是非一度お試しください！

２．中央値とは

中央値もまた、その名の通り「中央の値」のことです。“中央”を考えるためにデータに順序を入れなくてはいけません。通常、数値のデータに関しては、その数値の大小関係で順序を構成することができます。ひとまず、数値のデータが小さい順に並んでいるとしましょう。このときのちょうど真ん中のデータを中央値といいます。例えば、\(x_1<x_2<x_3\)の中央値は\(x_2\)です。このように、データが奇数個ある場合、ちょうど中央のデータが１つに定まりますが、\(x_1<x_2<x_3<x_4\)などの偶数個の場合、真ん中が、\(x_2\)か\(x_3\)か、定まりません。この場合、中央値として

\begin{align*}\frac{1}{2}(x_2+x_3)\end{align*}

を採用します。つまり、真ん中２つのデータの間を取って良しとするのです。これが中央値の定義です。
なお、「平均値」と「中央値」では圧倒的に「平均値」の方が、知名度が高いように思われます。これに歴史的な事情があります。平均値は、「とりあえずデータを全て足す」という計算がメインですが、中央値の場合、今お話した通り、まずデータを小さい順に並べる必要があります。この「並び替え」という技術はコンピュータのない時代において、非常に面倒な作業でした。こうしたことから比較的単純に計算ができる「平均値」の方がメジャーになっていったわけです。
また、中央値のもつ情報は、ちょうど中央のデータ１つ（あるいは２つ）のみであり、平均値と比較してみると、情報量がはるかに少ないという特徴があります。

３．平均値とは（再訪）

さて、平均値の特徴について再び、別の視点で考えてみましょう。データの中心部を表すということは、各データから最も「近い」という性質を持つことは自然な考えだと思います。

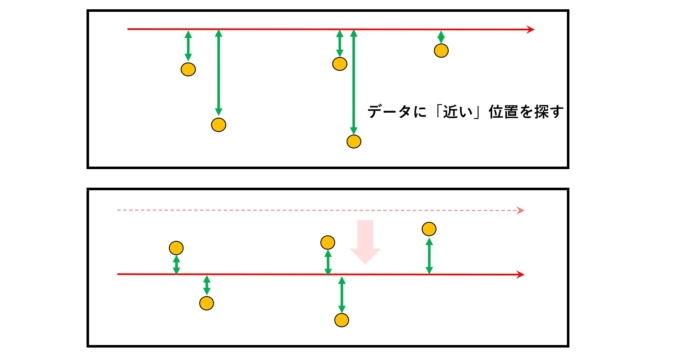
「近い」ということは、データとの差を考えますが、図のように大小関係をいちいち考えるのは面倒なので、一律で２乗してしまいます。これを「２乗誤差」といいます。この２乗誤差の和（つまりデータ全部との差）として次のような関数を考えます。

\begin{align*}f_1(x)=(x-x_1)^2+(x-x_2)^2+\cdots +(x-x_n)^2=\sum_{k=1}^{n}(x-x_k)^2\end{align*}

この関数が最小になるような\(x\)こそ、実は平均値\(\bar{x}\)なのです。
以下に最小になることの証明を描いておきます（読み飛ばしていただいても構いません）。

\begin{align*}\sum_{k=1}^{n}(x-x_k)^2 & =\sum_{k=1}^{n}(x-\bar{x}+\bar{x}-x_k)^2\\ &=\sum_{k=1}^{n}\left\{(x-\bar{x})^2+2(x-\bar{x})(\bar{x}-x_k)+(\bar{x}-x_k)^2\right\}\\ &=\sum_{k=1}^{n}(x-\bar{x})^2+2(x-\bar{x})\sum_{k=1}^{n}(\bar{x}-x_k)+\sum_{k=1}^{n}(\bar{x}-x_k)^2\\ &=n(x-\bar{x})^2+2(x-\bar{x})\sum_{k=1}^{n}(\bar{x}-x_k)+\sum_{k=1}^{n}(\bar{x}-x_k)^2\end{align*}

と変形します。このとき第２項の和は

\begin{align*}\sum_{k=1}^{n}(\bar{x}-x_k)=n\bar{x}-(x_1+\cdots +x_n)=0\end{align*}

となるので、

\begin{align*}f_1(x)=n(x-\bar{x})^2+\sum_{k=1}^n(\bar{x}-x_k)^2\end{align*}

つまり、\(f_1(x)\)は下に凸な２次関数となり、軸\(x=\bar{x}\)で最小値をとることが示されました。
また、補足しておくと、このときの最小値をデータの個数\(n\)で割ったものを「分散」と呼び、データの平均回りでのばらつきを表す指標になります。

\begin{align*}\textbf{データの分散}=\frac{1}{n}\sum_{k=1}^n(x_k-\bar{x})^2\end{align*}

４．中央値とは（再訪）

続いて中央値の特徴を別の視点から見ていきましょう。３節と同様に「データとの近さ」を考えます。先ほどは「差の２乗」を考えましたが、単純に絶対値を使った「差」を考えてもいいでしょう。つまり今回は

\begin{align*}f_2(x)=|x-x_1|+|x-x_2|+\cdots+|x-x_n|=\sum_{k=1}^n|x-x_k|\end{align*}

が最小になる\(x\)を考えます。そして何を隠そう、この最小をとる\(x\)の値こそ中央値なのです。その理由について具体的に3つのデータ\(x_1<x_2<x_3\)を考えてみます（読み飛ばしても構いません）。

絶対値の計算なので、いくつか場合分けをします。まず、\(x<x_1\)のとき

\begin{align*}f_2(x)=(x_1-x)+(x_2-x)+(x_3-x)=(x_1+x_2+x_3)-3x\end{align*}

\(x_1\leq x<x_2\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x_2-x)+(x_3-x)=(-x_1+x_2+x_3)-x\end{align*}

\(x_2\leq x<x_3\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x-x_2)+(x_3-x)=(-x_1-x_2+x_3)+x\end{align*}

\(x_3\leq x\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x-x_2)+(x-x_3)=(-x_1-x_2-x_3)+3x\end{align*}

となり、グラフにすると次のような形になります。

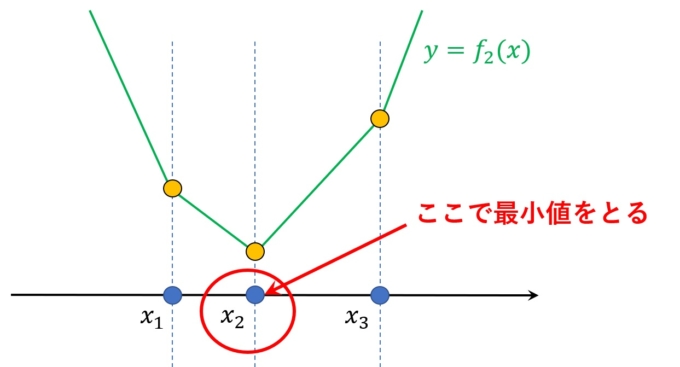
よって、\(x=x_2\)（中央値）のとき、\(f_2(x)\)は最小となります。奇数個のデータは全て同様に議論できます。では偶数個のデータの場合どうでしょうか。例えば\(x_1<x_2<x_3<x_4\)について考えてみましょう。先ほどと全く同じように場合分けを行います。まず\(x<x_1\)のとき

\begin{align*}f_2(x)=(x_1-x)+(x_2-x)+(x_3-x)+(x_4-x)=(x_1+x_2+x_3+x_4)-4x\end{align*}

\(x_1\leq x<x_2\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x_2-x)+(x_3-x)+(x_4-x)=(-x_1+x_2+x_3+x_4)-2x\end{align*}

\(x_2\leq x<x_3\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x-x_2)+(x_3-x)+(x_4-x)=(-x_1-x_2+x_3+x_4)\end{align*}

\(x_3\leq x<x_4\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x-x_2)+(x-x_3)+(x_4-x)=(-x_1-x_2-x_3+x_4)+2x\end{align*}

\(x_4\leq x\)のとき

\begin{align*}f_2(x)=(x-x_1)+(x-x_2)+(x-x_3)+(x-x_4)=(-x_1-x_2-x_3-x_4)+4x\end{align*}

となり、以下のグラフのようになります。

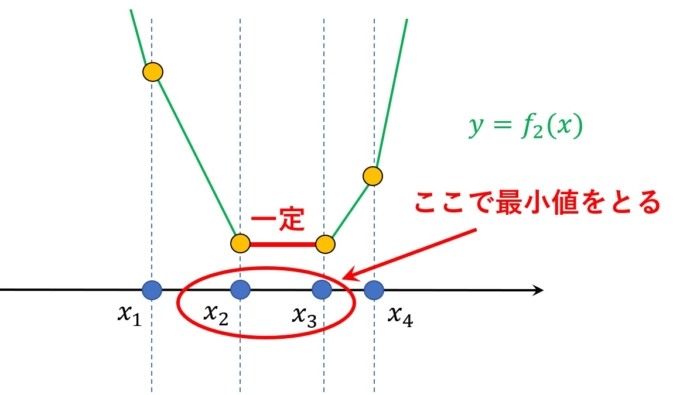
つまり、\(x_2\leq x\leq x_3\)において\(f_2(x)\)は一定値となり、どの点をとっても最小値となります。偶数個データがある場合は便宜上、この中心の値\((x_2+x_3)/2\)を採用します。

５．さいごに

いかがでしたでしょうか。今回の内容をまとめます。関数

\begin{align*}f_1(x)=\sum_{k=1}^{n}(x-x_k)^2\end{align*}

を最小にする\(x\)が平均値であり、関数

\begin{align*}f_2(x)=\sum_{k=1}^{n}|x-x_k|\end{align*}

を最小のにする\(x\)が中央値であるということをお話しました。何気なく使っている平均値や中央値の余り知られていない特徴付けです。このほかにもデータの特徴をとらえていくための様々な指標や数式が存在します。今回の内容についてわかりやすくまとめたものとして、心理統計学の名著【「心理統計学の基礎―統合的理解のために」南風原朝和(著) 有斐閣】があります。ぜひ興味のある方はご覧ください。