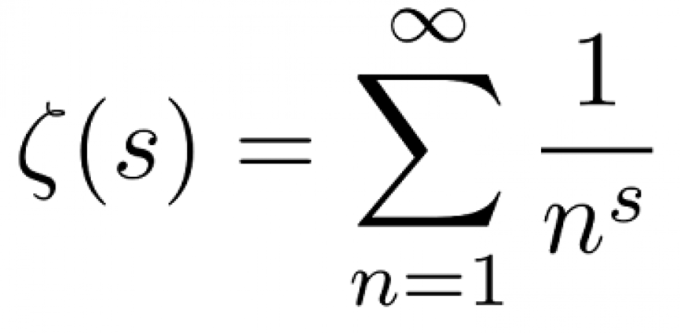和から講師の松中です。

昨年7月にオンラインの少人数数学ゼミである「ロマ数トレラン」を開講し、早くも一年が経ちました。本記事ではこれまでに開講されたロマ数トレランについてまとめてみたいと思います。

ロマ数トレランとは

「時間はかかってもいいから数学の美しさを中身からしっかり理解したい！」聞いているだけでわくわくする華やかなテーマが満載のロマンティック数学ナイト。その根底となる理論からしっかり学びたい。ロマ数トレランはそんな声から生まれました。ロマ数トレランは、ロマン溢れる数学を語ることができる講師による、講義形式ではなく、双方向の対話に重きをおいた受講者参加型の少人数制ゼミです。実際に手を動かしたり、しっかりと質問、議論をする時間を設けることで内容を確実に理解することを目標とします。同じ気持ちをもった仲間と一緒に学んだ先には新しい数学の世界が待っています。

参考)ロマンティック数学ナイトとは

弊社が主催する数学のショートプレゼン大会です。ロマンティック数学ナイトに参加すると算数から、純粋数学、応用数学、お笑い数学など様々な分野、レベルのロマンあふれる数学プレゼンを聞くことができます。

参考)トレランとは

山を縦走する山岳レースを意味するトレイルランニングの略です。急坂は大変な時はありますが、いったん頂上に上がれば壮大な風景を楽しむことができます。数学も同じです！平坦な道も、下り坂も、そして時にはハードな時もありますが、頑張って登りきれば素晴らしい風景が広がっているのです！

過去のロマ数トレラン

この一年で17分野のロマ数トレランを開講しました。ここでまとめてみましょう。

カリー・ハワード対応から見る「プログラミング言語、論理システム、圏」(檜山先生)

数学の魅力の一つに、全然関係のないと思っていた別々の対象に不思議な対応関係がみつかる、というものがあります。「プログラミング言語、論理システム、圏」という3つの対象を対応付けるカリー・ハワード対応を学びました。

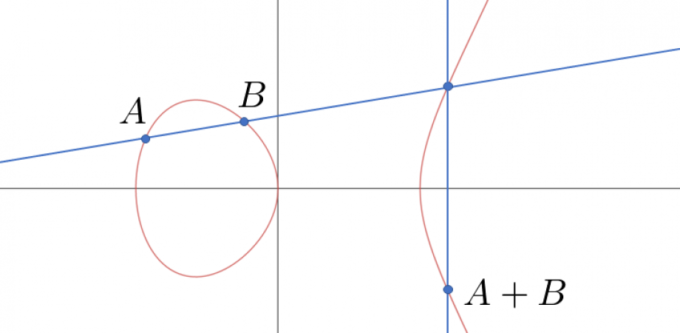
楕円曲線論入門オンラインセミナー(木内先生)

楕円曲線は数論と呼ばれる整数の研究分野に現れるとても魅力的で不思議な曲線です。楕円曲線はそれぞれが足し算に似た構造を持っており、その構造を特徴付けるモーデルの定理を証明しました。なかなか手計算が難しいテキストの演習問題をプログラムで解いた猛者もおりました。

ポアンカレ予想のはじまり－基本群を学ぼう－(佐々木先生)

ポアンカレ予想は唯一解決されているミレニアム懸賞金問題です。ポアンカレが創始したトポロジーの基本概念を学び、ポアンカレがどのような思考を経てポアンカレ予想にたどり着いたのか、ポアンカレ予想の真の意味を学びました。

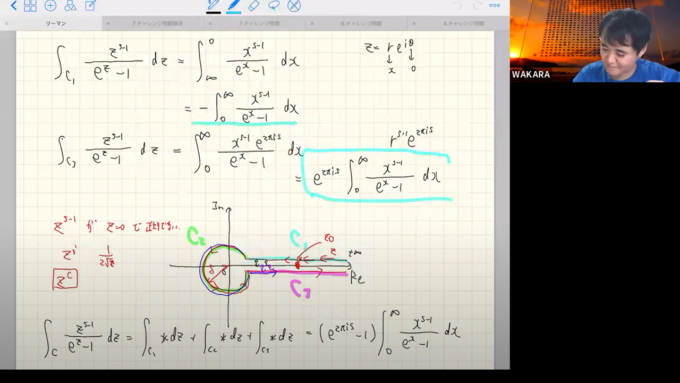
リーマン予想の主張を理解する～高校数学から始めるゼータ関数零点計算～(松中)

リーマン予想はミレニアム懸賞金問題の1つであり、160年以上もの間天才数学者たちを悩まし続けている数学界の難問です。本ゼミでは複素関数の基本を学び、エクセルを使ってゼータ関数の零点を実際に求めていきました。

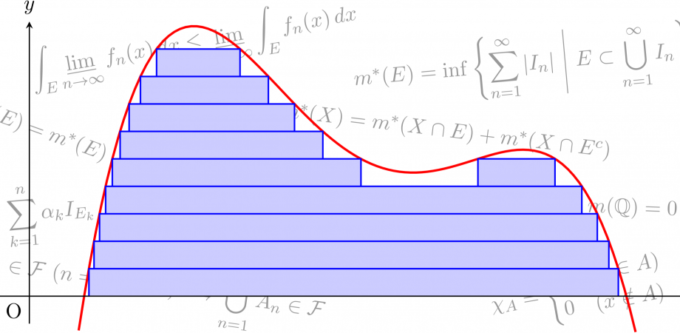
ルベーグ積分入門セミナー(山本先生)

高校で学ぶ積分はリーマン積分と呼ばれる積分ですが、関数解析や確率論などのより発展した数学を学ぼうとすると、リーマン積分とは別の切り口で定義された積分であるルベーグ積分が必要になります。本ゼミではルベーグの優収束定理の意味を理解し使えることを目標に掲げ、ルベーグ積分に一から入門しました。

マクスウェル方程式から電磁気学を学ぶ(石山先生)

マクスウェル方程式は電磁気学を学ぶ中でゴールのように扱われる存在ですが、本ゼミではマクスウェル方程式を出発点として様々な法則を証明していくという従来とは逆のスタンスをとっています。また石山先生が本ゼミを企画したのは特殊相対性理論への網渡しのためであり、電磁気学と特殊相対性理論の関係についても学びました。

ブラックホールと一般相対論入門セミナー(酒井先生)

本ゼミはブラックホールの周りで何が起こっているのかを数式から読み解けるようになることを目標としています。普通このあたりをしっかり勉強しようとすると前提の数学が難解であきらめてしまいがちですが、小林晋平先生の良書「ブラックホールと時空の方程式:15歳からの一般相対論」と、講師の酒井先生の工夫により、高校数学を学び直しながらブラックホールに挑みました。

ファイナンスのための確率微分方程式(坂本先生)

「数学は社会の役に立たない」といった声を聞くことがありますが、ファイナンスの世界では確率微分方程式を用いて価格を評価することが一般的です。確率微分方程式はファイナンス以外の分野でも使われる応用的な数学ですが、ビジネスマンが一人で学ぶのは大変です。本ゼミでは確率微分方程式の基本的な考え方と活用方法を学び、ビジネス書やファイナンス書籍を独自に読めるようにすることを目的として設計しました。

楕円曲線入門（有限体上の3次曲線、虚数乗法編）セミナー(木内先生)

楕円曲線入門セミナーに引き続き、より高度な楕円曲線の話題について学びました。ここで学んだ内容はヴェイユ予想、類体論などさらに高度でロマンティックな数学につながるものです。また本ゼミの理解にはガロア理論も必要で、ガロア理論についても演習問題をベースに学習しました。

微分トポロジー入門－高次元の世界を感じる－(佐々木先生)

私たちの世界は縦・横・高さの3次元の空間ですが、数学の世界は自由なのでもっと高次元の空間、その中の図形についても考えることができます。しかし2次元や3次元の図形と違い、目で見て形や性質を探ることができなくなってしまいます。本ゼミでは交差理論を用いて高次元の世界を調べました。

数学的な基本原理から量子論を学ぶ(本田先生)

物理分野は数学と異なり実験事実が正です。そのため今のところ正しいと思われている物理理論も、実験精度が上がった少し先の未来では正しくないことが判明するということも珍しくない世界です。一方数学の世界では公理と呼ばれる絶対的に正しいとされる命題が先に与えられており、そこから導けるものは全て正しいとします。この違いから数学好きが物理の本を読むと違和感や相性の悪さを感じてしまい読めないことが多くあります。本ゼミでは量子論を数学的に定式化し、数学好きでも違和感なく量子論を学べることを目指しました。

線形代数～入門からジョルダン標準形まで～(山本先生)

こちらのゼミは現在開講中です。純粋数学の分野でも統計、機械学習などの応用の分野でも重要な線形代数学を学んでいます。

一般相対論的宇宙論セミナー（Ⅰ）(酒井先生)

こちらも現在開講中のゼミで、一般相対性理論を用いて宇宙や物質の起源を学んでいます。テキストを3分割し、1クール目のゼミとなっております。理論的にはスッキリかけるような式も、実際に計算すると大量の計算が必要となり、講師も受講生も日々大量の計算を行っているように見受けられます。

アインシュタインの特殊相対性理論を原論文で読む(石山先生)

こちらも現在開講中のゼミです。特殊相対性理論を数式レベルで理解するだけではなく、アインシュタインの原論文を辿りながら、彼がどのような思考を辿って特殊相対性理論を生み出したのかを理解することにフォーカスしています。

素粒子物理学入門～超ひも理論への道～(酒井先生)

この夏開講する新ゼミです。「物質は究極的には一体何でできているのか？」という問いに数学と物理で挑んでいきます。

ロマ数トレラン講師とテーマ募集

この1年で様々な分野のロマ数トレランを開講してきましたが、数学、物理の世界には果てがありません。例えば解けば1億円がもらえるミレニアム懸賞金問題は全部で7問ありますが、これまでロマ数トレランで取り上げることができたテーマは「リーマン予想」と「ポアンカレ予想」の2問だけです。またその内容も証明を試みている最先端のお話しではなく、予想の意味を正しく理解したり、予想が生まれた当時の思想を辿るようなものであったりです。つまりまだまだ取り上げられていないテーマはたくさんあり、また同じテーマでもセミナーでの切り口は様々です。

そこでもし「自分が講師となってこんなロマ数トレランをやってみたい！」という方がおられましたら、是非一度お話をさせていただければと思います。以下のフォームよりお申込みお願いいたします。

ロマ数トレラン講師申込フォーム

また、「このテーマのトレランを開講してほしい」、「このテキストを仲間と一緒にガッツリ読み込みたい」というようなトレランのテーマに関しての要望も受け付けています。以下のフォームからご要望いただければと思います。過去開催のロマ数トレランの再実施希望についても受け付けます。

ロマ数トレランご要望、問い合わせフォーム

さいごに

ここ最近は物理系のロマ数トレランの開講が目立っておりますが、9月には佐々木先生による微分トポロジーや、著書多数の有名講師による純粋数学のゼミ(なんと2つ同時)の合計3ゼミを一挙開講する予定となっております。今後も魅力的なゼミをどんどん開講していきますので、メールによる開講情報のご案内が必要な方は、以下のフォームよりご登録ください。

新講座メールご案内登録

また、ロマンティック数学ナイトのPeatixまたはTwitterでも新講座のご案内をしておりますので、ご案内が必要な方はフォローをお願いいたします。

<文/松中>