毎年恒例2018年の年賀状問題の解答発表をさせていただきます。

今年は30名の方から解答のご応募をいただきました。
解答を送ってくださった皆様ありがとうございます！

そして見事、23名の方が正解しております。
正解者の方は本記事の最後でハンドルネームを発表させていただきます。

解答

まずは、問1)を再掲します。

このような問題は数式だけで解こうとするとなかなか大変です。プログラムを作って総当たりで確認された方も多いかもしれません。今回は、図、表を使って規則性を見つけることで解いてみましょう。

まず、下図のような表を用意します。6、7、8個入りのプチシューということで6がキーナンバーになりそうなため、表は0から35の数を6個ずつ区切って作成しています。

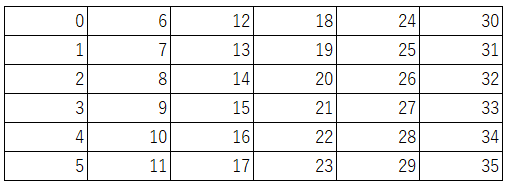
この表の中の数字で6個入りのプチシューをいくつか買うことで、ちょうど買える個数に緑色を塗ってみます。当然買うことができる個数は6の倍数になります。例えば6個入りのプチシューを3袋買うと、ちょうど18個のプチシューを買うことができますね。

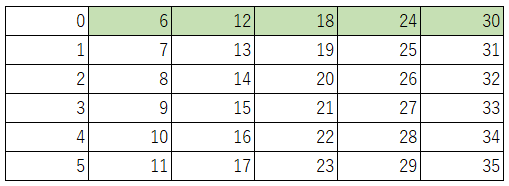
この時点で何も色が塗られていないマス目に入っている数は、6個入りのプチシューだけではちょうど買う事のできないプチシューの個数になります。

次に、6個入りと7個入りのプチシューでちょうど買うことができるプチシューの個数に黄色を塗っていきましょう。ただし、既に緑色で塗られているマス目はちょうど買えることがわかっているので、黄色で上塗りしません。

まず、7個はちょうど買うことができますので、7のマス目に黄色を塗ります。

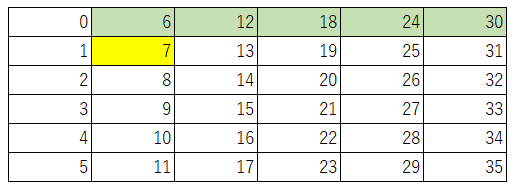
ちょうど7個買ったときに、さらに6個入りのプチシューを買っていくことで、7+6で13個、13+6で19個、19+6で25個のプチシューをちょうど買うことができます。この表は数を6個ずつ区切って用意していたため、7の右横の数を次々に黄色で塗ることができます。

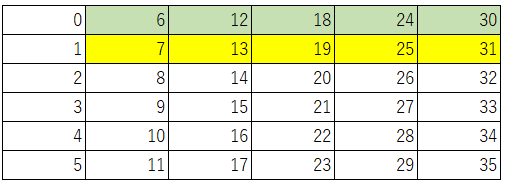
そして、7個入りのプチシューを2袋買う事で、14個のプチシューを買う事ができ、

先ほどと同様に、14の右横の数も次々に黄色で塗ることができます。

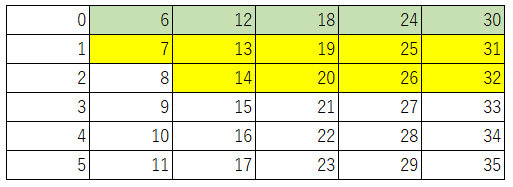
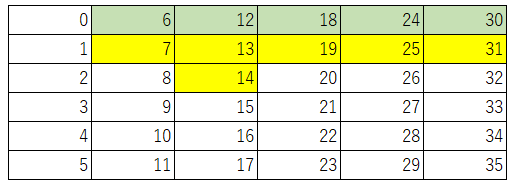
同様に、21(=3×7)個のプチシュー、28(=4×7)個のプチシューを買う事ができ、それらの右横の数も全て黄色で塗ることができます。

この時点で、買う事のできないプチシューの個数がかなり絞り込めました。

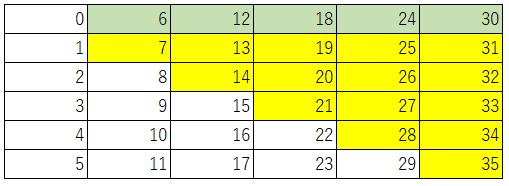
それでは最後に8個入りのプチシューも追加してみます。6、7、8個入りのプチシューの組み合わせでちょうど買うことができるプチシューの個数にオレンジ色を塗っていきましょう。

まず、当然8はオレンジ色に塗れます。

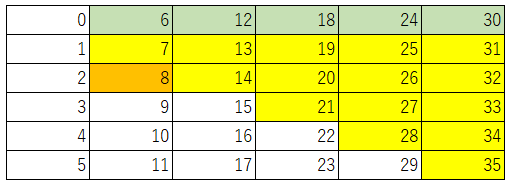
2列目でちょうど買うことのできる、6、7、8それぞれに対して、8を足すと3列目の14、15、16になります。まだ色がも塗られていない16をオレンジ色に塗ります。

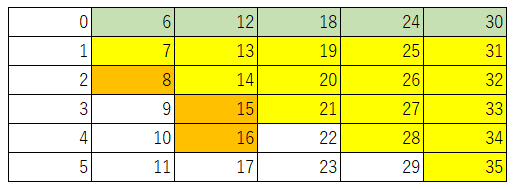
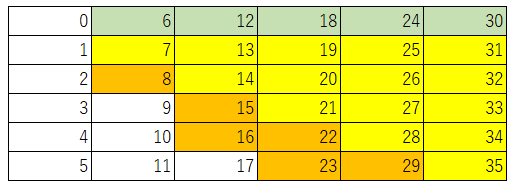
そして、3列目で色を塗られている12～16に対してそれぞれ8を足して、4列目、5列目もオレンジ色に塗っていきます。最終的に下図のようになり、色が塗られていないマス目の最大の数、つまり17が問1)の正解となります。

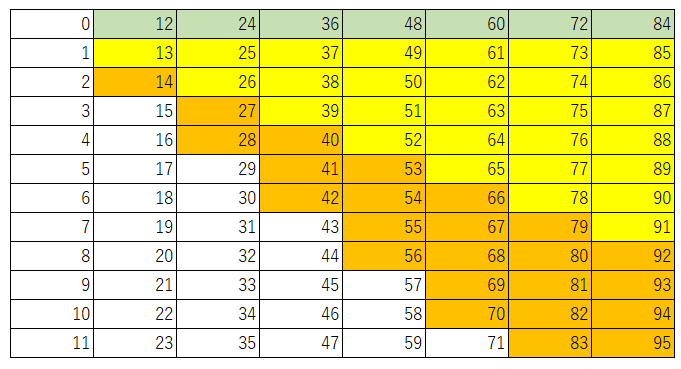
問2)も同じ方法でやってみましょう。問2)も再掲します。

問1)だけでは規則性が見えにくいですが、同じ方法で問2)を解くことで目に見える形で色塗りの規則がはっきり分かります。

最終的な結果は下の図となり、71がちょうど買う事のできないプチシューの最大数であることがわかります。黄色、オレンジ色がそれぞれ1段、2段の階段になっていて、とても綺麗ですよね。

以上まとめて、問1)は17、問2)は71が正解になります！

正解者発表！

正解した23名の方は以下の方々です！

・せっきー
・てつ
・kirby3
・フジテレビ鈴木
・fruition
・ユーリ
・進藤さん
・なべしー
・もずくん
・たっざえ
・hama-yasu
・omori
・reatn728
・佐々木さん
・いのうえ
・まこぴ～
・touch
・しもちゃ
・しょうすけ
・仙台の粒子
・Luca
・峯藤さん
・Belserg

正解者の中から抽選で3名の方に図書カード1,000円分を贈らせていただきます。

不正解だった方も、応募されなかった方もありがとうございました。

それではまた来年お会いしましょう！