現代社会における“必須科目”！？未来の技術を読み解く共通言語「線形代数」を学ぼう！

公開日

2025年11月19日

更新日

2025年11月14日

みなさんこんにちは！和からの数学講師の岡本です。今回は、AIやデータサイエンスの発展により、今や「現代の必須科目」となった線形代数（せんけいだいすう）について、その学習の重要性と、具体的な応用例、そして和からの効果的な学習法をご紹介します！

▼【開講中！】線形代数講座の詳細・お申し込みはこちら▼

1から始める大人のための大学数学入門-線形代数の基礎と応用-

この記事の主な内容

現代の必須科目！なぜ今、線形代数を学ぶべきなのか？

「線形代数」と聞くと、学生時代に習った行列やベクトルの難解なイメージが先行しがちです。しかし、線形代数こそが、情報社会を支える最も重要な数学の道具です。AI、ビッグデータ、コンピューターグラフィックス（CG）、画像認識、検索エンジンのアルゴリズムなど、現代の革新的な技術のほとんどが、線形代数の理論を基盤として動いています。

線形代数を学ぶことは、単に数学の知識を増やすことではありません。それは、多次元の情報をシンプルに捉え、論理的に処理する「思考のOS」をアップデートすることに他なりません。複雑で大規模な問題も、ベクトルと行列という統一された視点から見つめ直すことで、解決への道筋が驚くほど明確になります。線形代数は、文系・理系を問わず、現代の知的な活動を支える共通言語なのです！

１．線形代数が応用されている身近な例とその役割

線形代数は、私たちの日常のデジタル体験の裏側で絶えず活躍しています。代表的な応用例と、そこでの線形代数の役割を見てみましょう。

①AI・機械学習（ディープラーニング）

AIの処理は、入力データ（画像や音声）をベクトルとして捉え、ニューラルネットワークと呼ばれる層を通過させます。この層を通過する際の重みづけや変換の計算は、すべて行列の掛け算（線形変換）によって実行されています。線形代数がなければ、ディープラーニングは成立しません。

②画像処理・コンピューターグラフィックス（CG）

スマートフォンで写真を加工したり、ゲームや映画のCGを見たりする際、色の情報（RGB）や、3次元空間上の点の位置はベクトルで表現されます。画像の拡大・縮小、回転、遠近法の適用といったあらゆる操作は、行列の掛け算によって瞬時に、かつ正確に処理されています。行列を操作することが、画像を操作することに直結するのです。

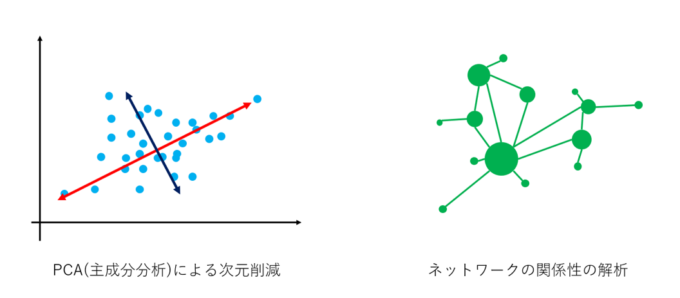
③データ分析・統計（主成分分析）

大量の多次元データから、そのデータの本質的な特徴や、最も影響力の大きい要素を抜き出す手法として主成分分析（PCA）があります。これは、線形代数の核となる固有値・固有ベクトルの考え方を使って実行されます。データの中に潜む「最も重要な方向」を客観的に見つけるために、線形代数が不可欠なのです。

④検索エンジン・レコメンドシステム

Googleなどの検索エンジンがページを評価するアルゴリズムや、AmazonやNetflixがユーザーにおすすめを表示するレコメンドシステムにも、線形代数の行列演算が深く関わっています。大量のユーザーとアイテムの関係性を行列で表現し、その重要度や相関性を分析しているのです。

２．難解なイメージを乗り越えるための和からの学習法

線形代数は、その重要性にもかかわらず、抽象的な概念（線形独立、基底、次元など）が多く、独学で挫折しやすい分野でもあります。和からの「線形代数講座」は、この学習のハードルを下げることに徹底的にこだわりました。

本講座では、「なぜその計算をするのか」「行列やベクトルが現実世界で何を意味するのか」という数学的な意味と背景を、図や具体例を多く使いながら丁寧に解説します。単なる計算練習ではなく、「多次元空間を理解するための直観力」を養うことを重視することで、実務で応用できる生きた知識として定着させます。高校数学の内容から不安がある方でも、個別指導形式で基礎からしっかりとフォローします。