箱ひげ図で学ぶデータのばらつき-第1回:一本の箱で“データの性格”が丸わかり【統計学をやさしく解説】
公開日
2025年11月18日
更新日
2026年1月5日

この記事の主な内容
はじめに:平均だけでは見えない“データの顔つき”
ビジネスデータを見るとき、多くの人がまず確認するのは「平均値」です。しかし、平均だけではデータの性格はほとんどわかりません。そこで大きな力を発揮するのが箱ひげ図です。箱ひげ図は、データがどんな広がり方をしているのか、どこが中心なのか、そして極端な値があるのかを、たった1つの図で表せる非常に便利なグラフです。
この記事では、箱ひげ図の読み方を、ビジネスパーソンの初心者にもわかるようにやさしく解説します。
箱ひげ図とは?:まずは形から覚える
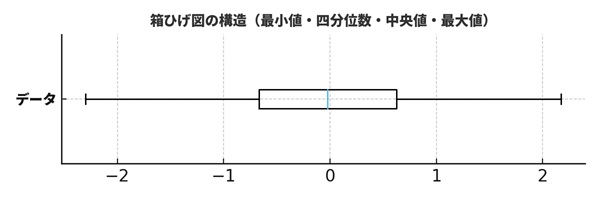
箱ひげ図は、データの「散らばり」をひと目で表すためのグラフです。次の5つの値を使って構成されます。
・最小値(Minimum)
・第1四分位数:Q1(下位25%地点)
・中央値:Median(50%地点)
・第3四分位数:Q3(上位75%地点)
・最大値(Maximum)
このうち、Q1とQ3に挟まれた部分が「箱」になり、中央値を示す線が箱の中に引かれます。箱の上下に伸びる線が「ひげ」で、データのおおよその範囲を示しています。
● 箱が表す意味
箱の大きさは、「データの真ん中50%がどれだけ広がっているか」を表します。箱が長ければばらつきが大きく、箱が短ければデータが比較的まとまっていることを意味します。
● 中央値がずれている意味
箱の中心に引かれた線が中央値です。中央値が箱の中央から上にズレていれば「低い値側にデータが多い」、逆に下にズレていれば「高い値側にデータが多い」という傾向が分かります。つまり、箱の中で中央値がどこにあるかを見ることで、「どちら側にデータが寄っているか」を直感的につかむことができます。
平均・棒グラフでは気づけないことが見える
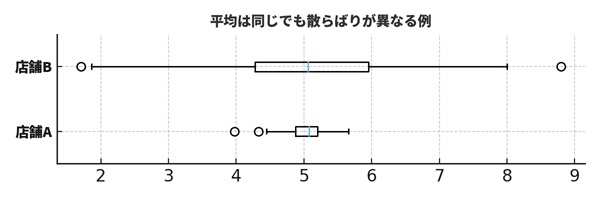
例えば、2つの店舗AとBの1日の売上平均がどちらも「5万円」だとします。しかし、実際には次のような違いがあるかもしれません。
・店舗A:毎日ほぼ4.5〜5.5万円で安定している
・店舗B:3万円の日もあれば8万円の日もあり、ばらつきが大きい
平均だけを見ると「どちらも5万円の店」として同じように扱ってしまいますが、実態はかなり違います。ここで箱ひげ図を使うと、店舗Aは箱もひげも短く「安定した売上」であることがわかり、店舗Bは箱やひげが長く「日によるバラつきが大きい店」であることが一目で分かります。
このように、箱ひげ図は「平均値では見えない違い」を視覚的に見せてくれるので、ビジネスで安定性やリスク、傾向を把握するのに非常に役立ちます。
四分位数をやさしく理解する
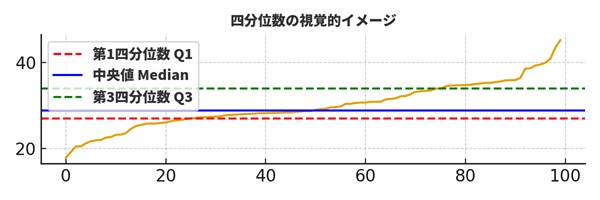
箱ひげ図を読み解くうえで重要なのが四分位数(しぶんいすう)です。少し難しそうな言葉ですが、考え方はシンプルです。
・Q1:データを小さい順に並べたときの下から25%地点
・中央値:ちょうど真ん中(50%地点)
・Q3:上から25%を除いた地点(全体の75%地点)
つまり、Q1〜Q3の範囲は「データの真ん中50%がどこに集まっているか」を表しているにすぎません。「四分位数」という専門用語に身構える必要はなく、「データを4つに割ったときの区切り」と理解すれば十分です。
実例で理解しよう:従業員の年齢を箱ひげ図にしてみる
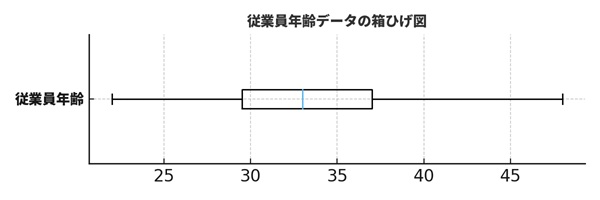
例えば、ある会社の従業員20名の年齢を調べて、箱ひげ図を作ったとします。その結果が次のようなイメージだったとしましょう。
・中央値:31歳
・Q1:28歳、Q3:36歳
・最小値:22歳、最大値:48歳
● ここからわかること
・真ん中50%の従業員は、おおよそ28〜36歳に集中している
・20代後半〜30代前半の人が多い会社だと分かる
・最大値48歳の「ベテラン層」が少数いる
このように、箱ひげ図を見るだけで「年齢層の分布」が一発でイメージできます。一方で、「従業員の平均年齢は30.8歳です」とだけ言われても、若手が多いのか、ベテランが多いのか、どれくらい偏りがあるのかまでは分かりません。
箱ひげ図は、数字の一覧や単なる平均値よりも、「この集団はどんなメンバーで構成されているのか?」を直感的に教えてくれます。
箱ひげ図は“データの性格診断”ツール
ここまで見てきたように、箱ひげ図は次のような情報を1つの図でまとめて教えてくれます。
・中心(中央値)がどこにあるか
・ばらつき(箱の長さや、ひげの範囲)がどれくらいか
・偏り(中央値が箱の中央からズレているかどうか)
・極端な値(外れ値)が存在するかどうか(※外れ値の詳細は次回解説)
たった1つの図で、データの性格を丸ごと把握できるため、レポート作成、現状分析、施策の効果検証など、さまざまなビジネスシーンで活用できます。
「平均値しか見ていなかった」という人ほど、箱ひげ図を使い始めると、データの見え方がガラッと変わるはずです。
次回予告:1.5倍ルールで外れ値を見つける
第1回では「箱ひげ図の読み方」を中心に、データの散らばりをざっくりつかむ方法を紹介しました。次回の第2回では、箱ひげ図のハイライトともいえる「外れ値の見つけ方」をさらに詳しく解説します。
・IQR(四分位範囲)とは何か
・1.5×IQRルールはなぜ使われるのか
・実際のデータで外れ値をどう見つけるか
ビジネスで「この数字だけおかしくないか?」「この異常値は無視していいのか?」と迷う場面で役立つ考え方の土台になります。ぜひ続けて読んでみてください。














