はじめに：外れ値はどこから「外れ」なのか？

データ分析をしていると、他の値から明らかに離れた“飛び抜けた値”が現れることがあります。これが外れ値（Outlier）です。

外れ値はときに、ミスの可能性であり、ときに重大なビジネスチャンスのサインでもあります。そこで重要なのが、箱ひげ図で使われる1.5×IQRルール。外れ値の判定基準として、最もよく使われる方法です。

この記事では、初心者でも迷わず使えるよう、1.5倍ルールを「図解で直感的に理解できる」レベルまで分解して解説します。

---

IQR（四分位範囲）とは？まずはここから

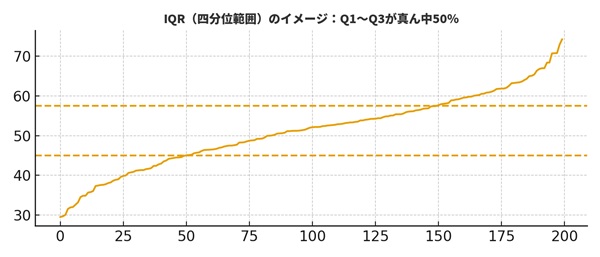
箱ひげ図で外れ値を考えるときに重要なのが、IQR（Interquartile Range）＝四分位範囲です。これは、次の式で表されます。

IQR = Q3（第3四分位数） − Q1（第1四分位数）

IQRは「データの真ん中50％がどれくらい広がっているか」を表しており、ばらつきの強さをつかむ指標です。IQRが大きいとデータの広がりが大きく、小さいとデータがまとまっています。

ポイントは、外れ値判定はこのIQRを基準にして行うということです。

---

外れ値判定ルール：1.5×IQRで線を引く

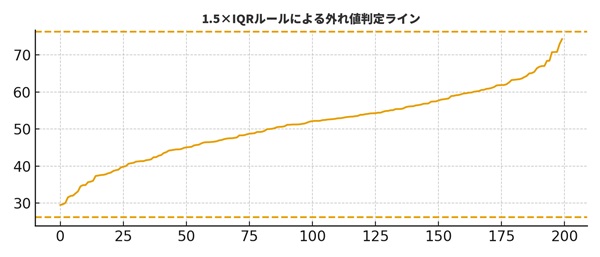
外れ値を機械的に判定するときに使うのが、1.5×IQRルールです。

具体的には、次の範囲を「通常の値」とみなします。

下側の下限： Q1 − 1.5 × IQR
上側の上限： Q3 + 1.5 × IQR

この範囲を飛び出したデータは、外れ値として扱います。

● なぜ1.5なのか？

1.5という数字には、細かい数学的な“きっちりした理論”というよりも、「経験的に使われてきた実用的な基準」という性質があります。

・1.0だと厳しすぎて、外れ値と判定される点が多くなりすぎる
・2.0だと緩すぎて、本当におかしな値を見逃してしまう可能性が高くなる

その中間として、“極端に離れた値”をほどよく拾える数字が1.5であり、長年にわたって広く採用されていると考えられます。

---

外れ値がある箱ひげ図の例

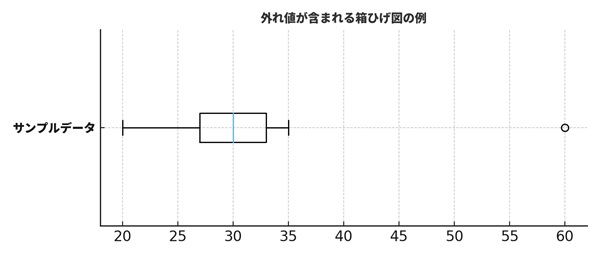
たとえば、次のようなデータを考えてみます。

[20, 22, 25, 27, 28, 29, 30, 31, 32, 33, 34, 35, 60]

ほとんどの値は20〜35の範囲におさまっていますが、60だけが極端に大きい値になっています。

このデータで箱ひげ図を作ると、60は箱とひげから大きく離れて「点」でプロットされ、外れ値として表示されます。

箱ひげ図は、数値を眺めているだけでは気づきづらい「飛び抜けた値」を、一目で見つけられるのが大きな強みです。

---

実データで外れ値を判定してみよう

それでは、実際に1.5×IQRルールで外れ値を計算してみましょう。先ほどのデータを使います。

[20, 22, 25, 27, 28, 29, 30, 31, 32, 33, 34, 35, 60]

● Step1：四分位数を求める

・第1四分位数 Q1 = 27
・第3四分位数 Q3 = 34

● Step2：IQRを計算

IQR = Q3 − Q1 = 34 − 27 = 7

● Step3：外れ値の範囲を計算

・下側の下限：27 − 1.5 × 7 = 27 − 10.5 = 16.5
・上側の上限：34 + 1.5 × 7 = 34 + 10.5 = 44.5

● Step4：範囲をチェック

16.5〜44.5の範囲に入らない値は、外れ値とみなされます。

→ この条件に当てはめると、60は外れ値であることが確定します。

このように、数式で計算しても、箱ひげ図として見ても、同じ値が外れ値として判定されることがわかります。

---

1.5×IQRルールは万能ではない（注意点）

外れ値判定のルールは便利ですが、万能ではありません。ビジネス現場で使うときには、次のようなポイントに注意が必要です。

● ① サンプル数が少ないと判断が不安定

データ数が少なすぎると、四分位数そのものが偏りやすくなり、外れ値判定の結果も安定しません。あくまでも「十分なサンプルがある」ことが前提だと考えましょう。

● ② “本当に重要な値”を外れ値として扱ってしまうことも

・売上が普段の2倍になった日
・特定店舗だけ異常に高い売上を記録しているケース
・新商品リリース直後の一時的な急増

これらはたしかに他の日から大きく外れているため、外れ値として検出されます。しかし同時に、「なぜこうなったのか？」を深掘りすることで、新たな成功パターンやリスクの兆候が見つかる可能性もあります。

● ③ データの分布によっては1.5倍が適さない場合も

・右側に長い“尾”を持つ分布（右に長い売上分布など）
・システム特性によって、定期的に大きな値が出るデータ

このような場合、1.5×IQRルールだけに頼ると、「仕様上当然の値」まで外れ値と判定してしまうことがあります。状況によっては、別の統計手法や業務知識と組み合わせて判断することが重要です。

---

まとめ：外れ値は“見つける”だけでなく“判断する”ことが重要

1.5×IQRルールは、外れ値を手早く、客観的に見つけるための、とても便利な方法です。ただし、ビジネスで外れ値をどう扱うかは、分析の目的によって変わります。

・エラーとして除外するべき値なのか？
・詳しく調べるべき重要なシグナルなのか？
・新しいビジネスチャンスや重大なリスクの予兆なのか？

次回の第3回では、こうした外れ値をビジネスでどう解釈し、どう扱うべきかを、判断の考え方＋実務で使える簡易テンプレ付きで解説していきます。

次回もぜひご覧ください。