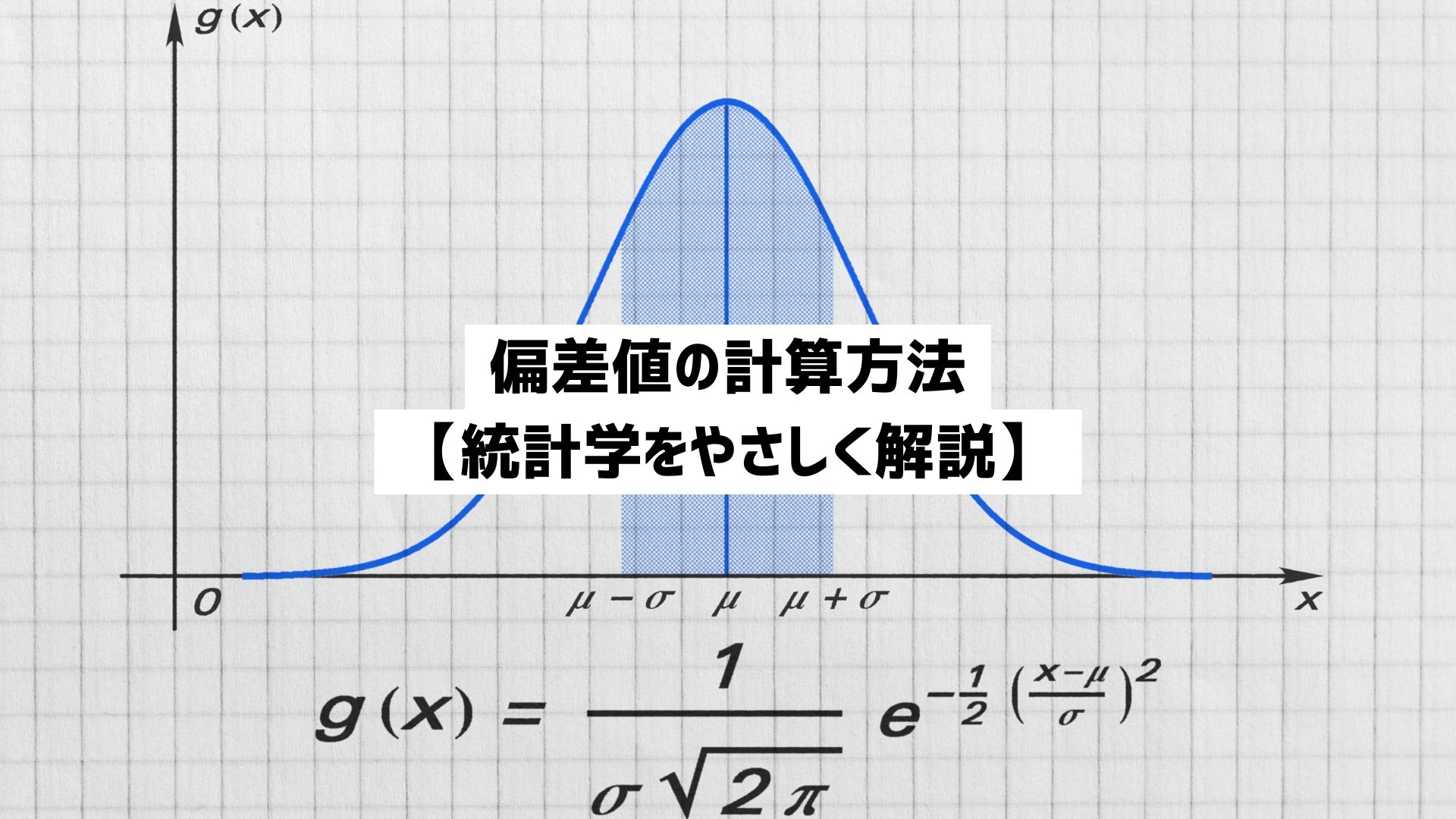
偏差値の計算方法【統計学をやさしく解説】
公開日
2022年12月6日
更新日
2024年8月4日
この記事の主な内容
偏差値とは
偏差値はテストの成績などでよく使われる値で、自分の成績がどのくらい良かったのかを数値化します。一般的には偏差値が\(50\)付近であれば平均的な成績で、それより高ければ良い成績、低ければ悪い成績と判断されます。偏差値を正しく解釈するには偏差値の計算方法や解釈の注意点を知る必要があります。以下のセクションでそれら確認しましょう。
偏差値の計算
偏差値の計算方法は以下の通りになります。
\(\frac{x-\bar x}{s}*10+50\)
\(x\)が自身の点数、\(\bar x\)が点数の平均値、\(s\)が点数の標準偏差です。
この式から分かるように、自身の点数が極端に低かったり高い場合には偏差値がマイナスになったり\(100\)を超えることがあります。興味がある方はこちらの記事を確認してください。
また、\(x-\bar x\)は自身の得点の平均からの距離であるため、\(\frac{x-\bar x}{s}\)は平均からの距離が標準偏差の何倍あるかを示しています。そのため、別の見方をすると偏差値は得点のデータを平均が\(50\)・標準偏差が\(10\)となるよう変換したデータであると解釈できます。従って、元のデータの分布と偏差値の分布の形は同じになります。
偏差値の解釈
偏差値が特にテストの得点を表すのに用いられるのは、点数が平均を中心に山型になっていることが多いためです。この分布のことを正規分布と言います。得点の分布が正規分布に従うとき、以下のような性質があります。
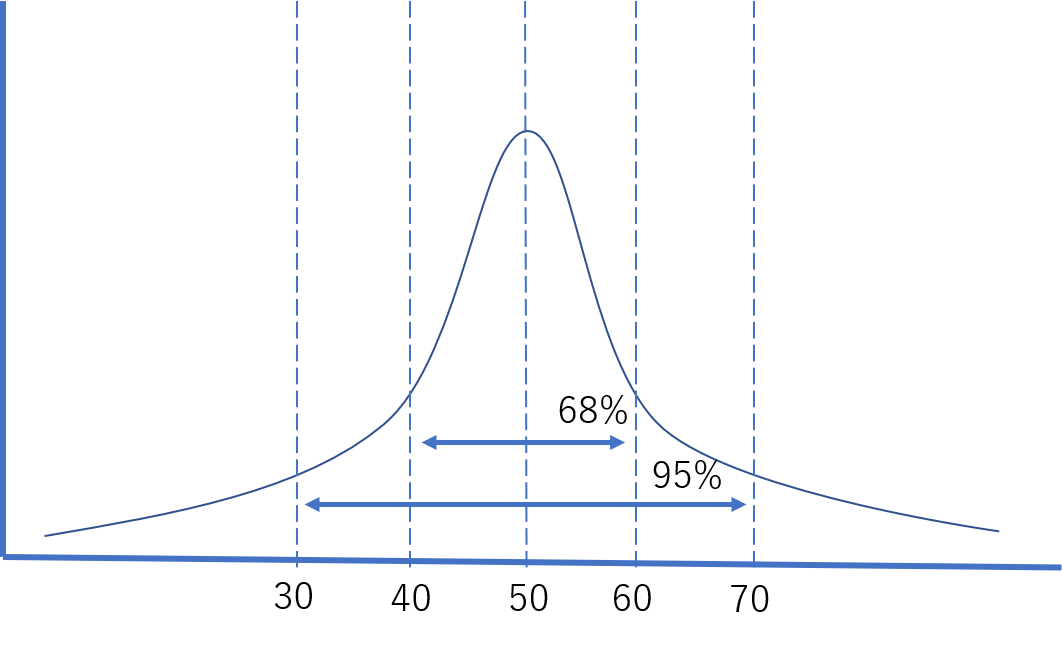
上のグラフの横軸は偏差値、縦軸は人数です。得点が正規分布に従うとき、偏差値も正規分布に従います。そのため、次のようなことが分かります。偏差値が\(40\)~\(60\)の受験者は全体の約\(68\)%であり、偏差値が\(30\)~\(70\)の受験者は全体の約\(95\)%います。このことを念頭に踏まえると、自身の偏差値から受験者の中での立ち位置を確認することができます。
例えば、偏差値\(70\)を取ったときには上の結果から自身が上位\(2.5\)%に入っていると分かります。偏差値\(30\)以下の受験者と偏差値\(70\)以上の受験者が全体の\(5\)%\((=100\)%\(-95\)%\()\)いるため、偏差値\(70\)以上の受験者は全体の\(5\)%\(÷2=2.5\)%存在します。ほとんどのテストでは平均値周辺の点数を取ることが多くまばらに分布しているため、自身の立ち位置が簡単に可視化される偏差値が有用になります。
偏差値の活用
偏差値を計算する際に元の点数から平均を引いて標準偏差で割りました。このように、データから平均を引き標準偏差で割る作業のことを標準化とよびます。標準化を行うことによって特にデータが正規分布である場合には標準化したデータが平均\(0\)、分散\(1\)の標準正規分布に従います。標準化したデータを用いることで統計的検定という分野で用いられる棄却域の計算が簡単になったり、統計学における式変形が楽になるなどのメリットがあります。標準化を用いてデータを簡単にする一例として偏差値を理解して、読み取れるようにしましょう。
●お問い合わせフォームはこちら
<文/須藤>












