条件付確率とは

条件付き確率はある事象が発生した条件で他の事象が発生する確率のことです。通常確率というと単純にある事象が起こる確率のことを想像しますが、条件付き確率ではある事象が発生したことが分かっているため異なる解釈と計算方法が必要です。この記事では条件付き確率の考え方と求め方、そしてベイズの定理を紹介します。

条件付き確率の解釈と計算

条件付き確率とは、ある事象が起こったという条件の下で異なる事象が起こる確率のことでした。例えば、サイコロを振ることを考えます。偶数が出る事象を条件づけたとき、サイコロの目が\(3\)以下である条件付き確率を考えます。この条件付き確率は単に\(3\)以下の数字が出る確率とは計算されません。
はじめに、なにも条件づけずに\(3\)以下の数字が出る確率を考えてみると\({1,…,6}\)から\({1,2,3}\)を選ぶ確率なので\(\frac{3}{6}=\frac{1}{2}\)と計算されます。
次に、条件付き確率について考えます。偶数が出る事象が条件つけられているので、出目は\({2,4,6}\)のいずれかとわかります。このうち、\(３\)以下であるのは\({2}\)のみであるので確率は\(\frac{1}{3}\)となります。

では、なぜこのように確率が異なるのでしょうか。条件づける事象を\(A\)、もう一つの事象を\(B\)とします。通常、事象\(B\)の確率を求めるとき我々は全事象（起こりゆるすべての場合）に対して\(B\)の起こりやすさを考えます。対して、条件付き確率では事象\(A\)が起きた時の事象\(B\)の起こりやすさを考えます。

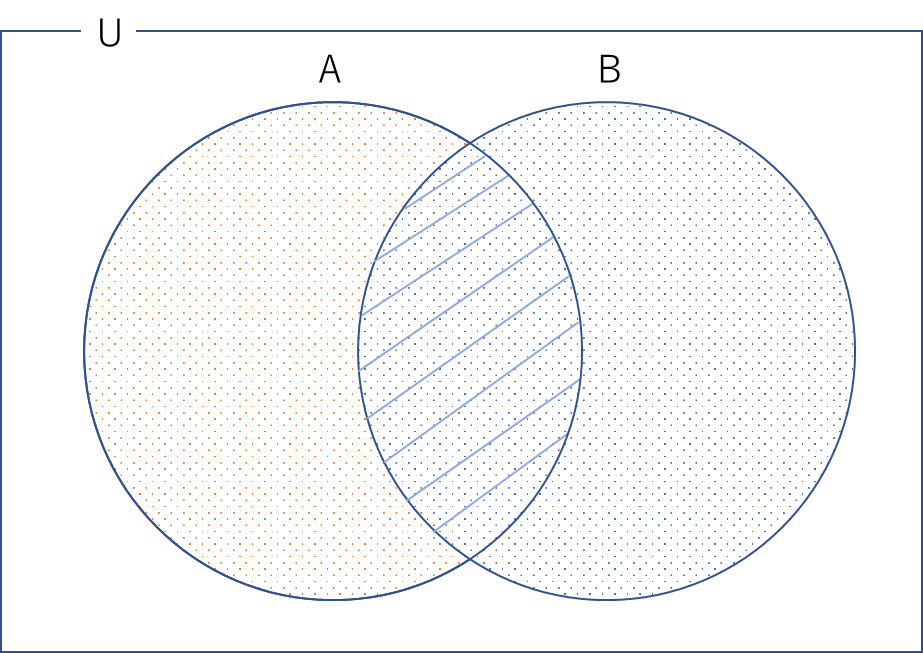
通常の確率では、上図の赤点の領域が全事象\(U\)に対してどの程度起こりやすいかを考えます。対して、条件付き確率では青線の領域が青点の領域に対してどの程度起こりやすいかを考えます。このように、条件付き確率を考える際は確率の対象となる事象自体が変わることを意識しなければなりません。

ベイズの定理

条件付き確率の活用としてベイズ統計学で用いられるベイズの定理が存在します。ベイズの定理は事象\(A,B\)に対して条件付き確率が以下のように計算できるという定理です。

\(P(A|B)=\frac{P(B|A)P(A)}{P(B)}\)

式の結果を見ると、\(B\)を条件づけたときの\(A\)の確率が\(A\)を条件づけたときの\(B\)の確率、\(A\)の確率、\(B\)の確率で表せます。ベイズ統計学は新しく得られた情報に基づいて確率を更新していくという特徴があります。例えば、ある大学に入学した学生の司法試験の合格率が前年度まで\(60%\)であったのが今年は\(80%\)であった場合にはその大学の学生の合格率は更新され、\(60%\)よりも高いものとなります。上の式では、\(P(A|B)\)が更新された確率であり事後確率と呼ばれます。また、\(P(A)\)は更新前の確率であり事前確率と呼ばれます。

上の例を用いると、\(A\)が司法試験に合格するという事象、\(B\)がある大学に入学するという事象となります。実際に合格した受験者がその大学の学生である確率\(P(B|A)\)とその大学の学生である確率\(P(B)\)も用いて、更新された事後確率\(P(A|B)\)が求められます。

条件付き確率の活用

条件付き確率は主にベイズの定理を通して統計学で用いられることが多いです。ベイズの定理を利用することで通常計算できない確率分布を簡単に近似することが可能になります。この手法を近似ベイズ計算と呼び、工学やファイナンスなど様々な分野で活用されています。

●お問い合わせフォームはこちら

<文/須藤>