塗り絵と数学~四色定理~
公開日
2022年6月23日
更新日
2022年6月23日
こんにちは。和からの数学講師の岡本です。今回は「塗り絵」に関する話題です
この記事の主な内容
1.塗分けるのに必要な色の数は?
まずは塗り絵を考えます。どんなに適当に塗っても言い訳ではなく、隣り合うエリアの色は別にして、うまく塗り分けなければならないとします。例えば下の図①のような塗り方はNGで、②はOKとします。
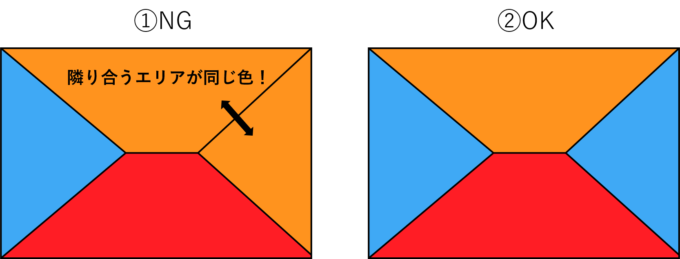
このような条件で塗り絵を行う場合、最低何色あればいいでしょうか?この素朴な問題は19世紀半ばに当時のイングランドの地図の塗り分けを考えていたフランシス・ガスリーらによるものが起源とされ、「4色あれば十分なのではないか」と予想されていました。その後、ド・モルガン、ハミルトン、ケーリーといった定理にその名を残す偉大な数学者たちによって徐々に定式化さていきます。例えば次の図は2色あれば塗り分けることができますし、

3色必要な場合や4色必要な場合もあるようです。
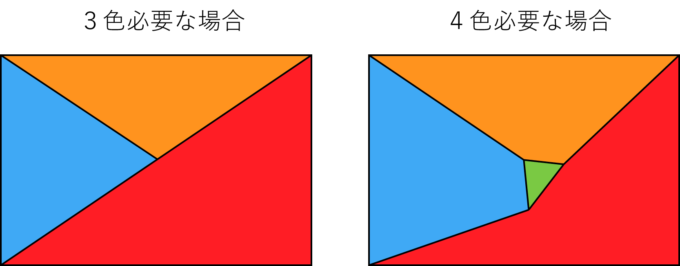
では、必ず5色必要な図はあるのでしょうか?塗り絵に寄らず、最低何色あれば十分なのでしょうか?いろいろと観察を続けると、やはり「4色あれば十分なのかもしれない」という結論に行き着きます。しかし、なかなかそのことを証明することができずにいました。
2.四色問題のはじまり
この問題は「四色問題」といわれ、長い間難問とされてきました。しかし、1879年にアルフレッド・ケンプによって四色定理の証明が発表されました。この業績からケンプは王立協会のフェローに選ばれ、後にロンドン数学会の会長に就任します。ここから10年近く解決されたと思われていましたが、1890年にパーシー・ヒーウッドにより証明の不備が指摘され、再び未解決問題となりました。

ケンプによる“誤植”は全く無駄なものだったのかというと、そんなことはありません。彼の論理に沿ってうまく修正を施すことで、「5色あれば十分」ということが証明されました。これを「五色定理」といいます(無意味な誤植ではなかったというシャレの効いた名前ですね)。というわけで、5色あれば十分であることが示されましたが、それが最小なのかどうかはまだ未解決です。4色必要な塗り絵は先ほど紹介したように具体例がすぐに思いつきますが、5色必要な場合は存在するのでしょうか?最低限必要な色の数が4なのか5なのかはこの時点ではわかっていませんでした。
4.四色問題の解決
そして物語が再び動き始めたのは1976年。ケネス・アッペルとヴォルガング・ハーケンは、コンピュータを用いた方法により、四色問題を肯定的に解決しました。つまり、平面上の塗り絵に必要な色の最小数は4であることが証明されたのです!コンピュータのバグの可能性も指摘されましたが、その後、手法の改良やコンピュータの性能向上により現在では四色問題は完全に解決されていると考えられています。補足しておくと、紙とペンだけを使った比較的簡潔な証明のことをしばしば“エレガント”な証明と呼ぶことがあります。しかし、こうした“エレガントな証明”はいまだになされていません。それに対して、現在知られている解法は、コンピュータを用いた、ある意味で「力技」ともいえる証明方法であり、これを“エレファント”な証明と揶揄することがあります。なかなかパンチが効いたシャレですね。
4.さいごに
いかがでしたでしょうか?どんな塗り絵や世界地図も4色あれば必ず塗り分けることができるという、驚愕の事実が数学やコンピュータサイエンスを用いることで証明されました。このように、証明までの道のりが険しいものの、得られる結果が非常にシンプルな定理ってなんだか美しいと思いませんか?(岡本は美しいと思うタイプです)
次回はこうした塗り分けの問題を、グラフ理論を用いて数学的に定式化することについて簡単に解説しようと思います!
和からではオンラインによる集団授業や個別授業も行っております。算数から数学、統計学まで幅広く対応していますので、興味のある方はまずは無料の個別カウンセリングへ!
●和からのセミナー一覧はこちら
●お問い合わせフォームはこちら
<文/岡本健太郎>















