※本記事はロマ数トレラン「数学的な基本原理から熱力学を学ぶ」の講師である本田耕一郎先生による熱力学の入門の記事になります。ご興味を持った方は是非ゼミにご参加ください。ガイダンス回は無料となっております。

始めに

熱は人間の活動の根源ともいえますが,これに関わる現象は地球上の生物や物質だけでなく宇宙にまで見ることが出来るマクロな現象です.熱現象を理解しようとするとき,一般に自然現象はミクロな世界の基本法則に支配されているだろうから, 熱のようなマクロな現象もミクロ系の運動法則で(量子論)で原理的には理解できるであろう. そして,あらゆることが予測できるだろうと期待されます.しかしながら物質を構成する莫大な(原子,分子などの)粒子数とその自由度を考えるとこれは大いなる幻想であることが解ります. 従ってマクロ系を取り扱うには別のマクロ系専用の理論体系が必要になるわけです.

この熱に関わる人間の長い経験と熱の本質を理解しようとする思索の末, クラウジウスやトムソンによって, 1850年以降「熱力学」という新しい物理学が作り出されました. 熱力学は熱が関与する物理法則を記述する理論で極めて強固な体系です. 今世紀の初頭の量子論の登場によってミクロな物理学が大変革を余儀なくされましたが, この熱力学の理論は全く変更を受けることがありませんでした.

熱力学は平衡状態と呼ばれる状態とその状態間の遷移に関する理論です. 熱力学の標準的な理論は熱現象に関わる経験的な事実から帰納的に導かれた熱力学の法則を前提として,これらの法則から諸々の熱現象の法則を演繹的に導き出します.

ここでは熱力学の基本法則を簡単に説明します.

1. 巨視的な記述

マクロ系

物理学では考察の対象となるものを系と呼びます.我々の身近にある物質は電子や原子などの構成要素数が莫大(マクロ)な数(例えば\(10^{24}\)個)で,しかもそれらは相互作用している系です.そのような系をマクロ系と呼びます.熱力学で対象とするのはこのようなマクロ系です.

マクロな物理量

系のマクロな振舞いを見るためにはマクロな物理量を考察の対象としますが,それは系全体のエネルギー,気体の体積やゴム紐の長さなどの幾何学的量, 気体の圧力\(P\)などミクロな物理量をマクロなスケールで平均した量,さらにミクロ系ではそもそも定義されなかった温度やエントロピー等になります.

エネルギー

マクロな物理量の中でもエネルギーを極めて重要で, 対象となる系の全エネルギー\(E\)は
\[
E=E(\mbox{全体運動})+E(\mbox{全体位置})+E(\mbox{全体内部})
\]
と, 分解できます. \(E(\mbox{全体内部})\)は内部エネルギーと呼ばれ, 物質を構成する分子等の運動エネルギーや相互作用のエネルギーの総和になります.

このようにエネルギーをもれなく合算した全エネルギーが保存されます.

熱力学で扱う状態

熱力学で扱うのは平衡状態です. 一般に外部と隔絶されたマクロ系を十分長い間放置すると,マクロに見る限り何も変化が起きない状態になります.このような状態を熱平衡状態,あるいは単に平衡状態と呼びます. 二つの状態を比較してマクロな物理量の値がマクロに見て無視できるほど小さければマクロに見て同じ状態といいます.そうでない場合は異なる状態といいます.

熱力学では平衡状態のマクロな性質と,一つの平衡状態から他の平衡状態へ移り変わる遷移だけを考察の対象とします.

2. 平衡状態を記述する変数

示量変数・示強変数

示量変数(相加変数)は熱力学を語る上での基本的な言葉になります.例えば気体が容器に閉じ込められている場合,この系をマクロな視点から特徴づけるのは容器の体積\(V\),物質量\(N\)になります.これらは実際に測定制御できる量です.もしほかの体積\(V^{\prime}\),物質量\(N^{\prime}\)の系を接触させ仕切りを取り除くと体積は\(V+V^{\prime}\),物質量は\(N+N^{\prime}\)となり元の系での対応する量の和になり,このような性質を相加的であるといいます.

体積\(V\)と物質量\(N\)はどちらも示量変数ですが両者には本質的な相違があり, 物質量は容器に密封すると変えることができませんが,体積\(V\)は力学的な操作によって制御が可能です. このように着目する系の外部にはマクロな力学的世界が存在することが前提となります.

一方,温度\(T\)や化学ポテンシャル\(\mu\)と呼ばれる量は示強変数と呼ばれます.マクロに見て均一な状態にある系に関して示強変数はどの部分も,その体積にかかわらず同じ値を持ちます. 示強変数は後述の, エントロピーやエネルギーの基本関係式(示量変数の関数)を微分して得られます.
　

平衡状態を記述する方法

平衡状態を記述する方法として, 示量変数のみを選択するか,そのうちの一つを示強変数(特に温度\(T\))で置き換えるという二つの流儀があります. ここでは平衡状態を示量変数だけの組で記述します. そしてエントロピーという量\(S\)の存在を前提とします.

単純系 基本関係式

マクロな系は外部からの影響を受け,更に相互作用(内部束縛)がある複雑な系ですが, これを内部束縛がない均一な部分に分割してこれを単純系と言います. 単純系のエントロピー\(S\)はエネルギー\(U\)といくつかの相加変数\(X(V:\mbox{体積}, N:\mbox{物質量など})\)の関数で
\[
S=S(U,X)
\]
と表せられます. これをエントロピー表示の基本関係式と呼びます. また,その関数の引数\((U,X)\)をエントロピーの自然な変数と呼びます. \(S\)の基本関係式は上に凸, 連続的に微分可能で, 特に\(U\)に関する微分係数は正であることが要求されます.下限は\(0\)で上限はありません.

系の平衡状態は示量変数の組\((U,X)\)で完全に指定できます. この示量変数の組\((U,X)\)で指定された各々の平衡状態にエントロピー値が一つ対応します. エントロピーは平衡状態でしか定義されません. \((U,X)\)を許されるすべての範囲でそれぞれ動かしたとき\((U,X)\)が作る数学的な空間を熱力学的な系の状態空間といいます. したがって,\(S\)は状態空間上で定義された関数であると解釈できます.

\(S\)は単調な増加関数ですので, 逆に\(U\)について解くことが出来き, エネルギー\(U\)表示の基本関係式\(U=U(S,X)\)が求められます. \(U\)の基本関係式は下に凸, 連続的に微分可能で, 特に\(S\)に関する微分係数は正であることが要求されます.

単純系の複合系 エントロピー最大の原理

単純系\(i\)のエントロピーの自然な変数を\(U^{(i)}, X^{(i)} (i=1,2,\cdots)\)として基本関係式を\(S^{(i)}=S^{(i)}(U^{(i)}, X^{(i)})\)とします. これらの単純系の複合系を考えると, 全ての単純系が与えられた条件下で平衡状態にあって, かつ
\[
\hat{S}=\sum_{i}S^{(i)}(U^{(i)}, X^{(i)})
\]
が最大になるとき,その場合に限り複合系は平衡状態になります. その時の複合系のエントロピーは\(\hat{S}\)の最大値になります.

状態量

各平衡状態に対して一義的に値が確定するような物理量(エントロピーやエネルギーなど)を状態量といいます.ひとつの平衡状態における状態量の値はその平衡状態にどのような過程で到達しても同じ値を持ちます.またある過程の前後での状態量の差は,その過程がどんなものであったかとは無関係に,最初と最後の平衡状態だけで決まります.

示量変数に共役な示強変数

エントロピー表示の基本関係式\(S＝S(X_0,X_1,\cdots X_t)\)(\(U=X_0\)と表記, \(X_1,X_2 \cdots \),は具体的には\(V\),\(N\)など)を示量変数で偏微分すると,
\[
\Pi_k(X_0,X_1,\cdots,X_t)\equiv \frac{\partial S(X_0,X_1,\cdots,X_t)}{\partial X_k}
\]
が得られます.これを示量変数\(X_k\)に共役なエントロピー表示の示強変数と呼びます.　　　　　

この表記により特に重要なエネルギーに共役な示強変数である逆温度\(B\)が
\[
B= \frac{\partial S}{\partial U}
\]
と,定義できます.

同様にエネルギー表示の基本関係式\(U＝U(X_0,X_1,\cdots X_t)\)(ここでは\(S=X_0\)と表記)を示量変数で偏微分すると,
\[
P_k(X_0,X_1,\cdots,X_t)\equiv \frac{\partial U(X_0,X_1,\cdots,X_t)}{\partial X_k}
\]
が得られます.これを示量変数\(X_k\)に共役なエネルギー表示の示強変数と呼びます.　
この表記により温度\(T\)が,エントロピーに共役な示強変数として
\[
T= \frac{\partial U}{\partial S}.
\]
同様に体積Vに共役な示強変数の符号を変えたものとして圧力が
\[
P\equiv -P_k=\frac{\partial U}{\partial V},
\]
物質量\(N\)に共役な示強変数\(P_N\)を化学ポテンシャルと呼び,
\[
\mu\equiv -P_N=\frac{\partial U}{\partial N}
\]
となります.

またエネルギー表示の基本関係式と共役な示強変数より, わずかに異なる平衡状態のエネルギー差を,
\[
dU=TdS−PdV+\mu dN + \cdots
\]
と展開することができます.

示量変数と示強変数(温度\(T\))を用いた基本的関係式の記述

さて,これまで系の熱力学的性質は\(S\)に関する基本関係式\(S=S(U, X)\)で完全に決定できることを述べてきました. また, \(S\)を\(U\)について解いて\(U\)の基本関係式\(U=U(S, X)\)を求めることができました. ここで基本関係式の引数である示量変数のうちの一つを示強変数(温度\(T\))で置き換えた表示を考えます.

平衡状態を組\((T,V,N)\)で与える基本関係式としてヘルムホルツの自由エネルギーと呼ばれる関数\(F=F(T,V,N)\)があります.

これは\(U＝U(X_0,X_1,\cdots X_t)\)をルジャンドル変換することにより
\[
F(T,V,N)\equiv \left[U(S,V,N) − ST\right](T, V, N)
\]
と結び付けられます. \(U−ST\)の値を\(T\),\(V\),\(N\)の関数として表したのが\(F(T,V,N)\)です. 各平衡状態について\(U−ST\)の値が一つに定まりそれが\(F\)であることを意味します. このヘルムホルツの自由エネルギーを用いると,「系がある状態から別の状態へ等温操作で移る際に系が外部に行う仕事の最大値は,二つの状態のヘルムホルツ自由エネルギーの差である」ことが分かり. ヘルムホルツの自由エネルギーは力学におけるポテンシャルエネルギーの役割をします.

3. 仕事と熱　熱力学第一法則

熱は人間に直接感知されるもので,歴史的にも直接認知されました. 17-18世紀に急速に進歩した温度計を媒介として熱と温度とが識別され,クラウジウスの実験を通して仕事と熱が同じものであるという認識に至り,これがエネルギー保存則へまとめられました.
着目する系に種々の状態変化を起こさせるには外部の条件を変える必要があります. そのために着目する系の外部に存在するマクロな力学的世界において, 着目する系と相互作用している外部の物体の座標を変化させます. (例えばシリンダーに閉じ込められた気体の系でピストンを操作して体積を変化させるようなことです.) その変化dxiに対して系になされる仕事は
\[
d^{\prime}W = \sum X_idx_i
\]
で与えられます.

この微小仕事の表現は一般には完全微分の形に書くことができません. 仕事は一般に経路に依存して状態量ではないからです.エネルギー保存の法則が成立することを要請すると,この仕事以外の形でエネルギーが付与されていることになります.

系のエネルギーが外部座標と系の状態に依存して定まっているならば,エネルギーは状態量ですから外部の微小な変化に対応する変化は完全微分になります.
\[
dU = d^{\prime}W+d^{\prime}Q.
\]
これが成立するために\(d^{\prime}Q\)が存在する必要がありこれを熱と呼びます. この式は熱の移動がエネルギーの移動の一つの形態であることを端的に示し熱力学の第一法則と呼ばれます.

さてピストンを押す速さが無限小の場合を考えます.この場合系は常に平衡状態にあり無限の時間をかけて変化してゆくと考えられます.このように系が常に平衡状態とみなせる過程を準平衡過程と呼びます.
系を容器に入った気体と考えて,この場合ピストンにかかる気体の圧力を\(P\),体積を\(V\)とすると
\[
　　　　　　　　　　　d^{\prime}W= -PdV,\,\,\,\,dU=d^{\prime}Q−PdV
\]
が得られます.

準静的過程では常に平衡状態にありますから,わずかに異なる平衡状態のエネルギー差の関係式が成立して,気体の粒子数に変化がない場合,
\[
dU=TdS-PdV
\]
となります. これが\(dU=d^{\prime}Q − PdV\)と一致しますから
\[
d^{\prime}Q=TdS
\]
となります. したがって準静的過程においては,系に外部から流れ込む熱量は系の温度と,系のエントロピーの変化の績に等しいことが分かります. これを変形して積分すると
\[
\Delta S =\int \frac{d^{\prime}Q}{T} \mbox{(準静的過程, 積分は始状態から終状態まで)}
\]
というエントロピーを定義する公式が得られます.

4. 熱力学的過程の不可逆性　熱力学の第二法則

熱力学では, “仕事が熱に変換される”過程,あるいは,“熱が高温から低温に移る” 過程は不可逆であるという経験事実を述べた命題を熱力学第二法則といいます. これから，“一様な温度をもつ,2つの熱源の間にはたらく熱機関の効率には上限が存在する” ことが結論されます.

熱力学第二法則の記述

第二法則はいくつもの言い表し方があります．

熱力学的過程の不可逆性について　カルノーサイクル,トムソンの原理,クラウジウスの原理

カルノーサイクルは,温度の異なる2つの熱源の間で動作する可逆な熱力学サイクルの一種でです.

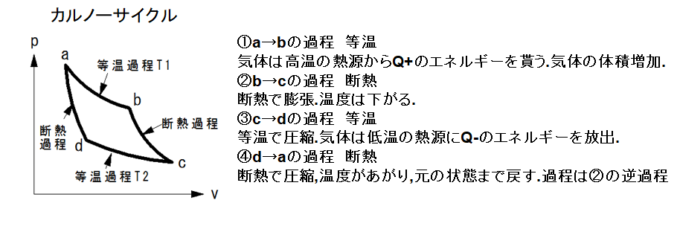
熱機関の効率を考えると熱機関の作業物質がサイクルにおいて外界に仕事\(W\)を行うときは,一般には,より高温の熱源から熱量\(Q^{+}(>0)\)を吸収し,より低温の熱源に熱量\(Q^{−}(>0)\)を放出します.作業物質が吸収する正味の熱量は\(Q=Q^{+}−Q^{−}\)であり，熱力学第一法則より\(W=Q^{+}−Q^{−}\)が成り立ちます.このとき,熱機関の効率\(\eta\)は,\(\eta=W/Q^{+}=1−Q^{−}/Q^{+}\)で熱機関の効率\(\eta\)は,一般に作業物質の熱力学的特性,熱源の温度やサイクルのさまざまな条件に依存して決まります.

熱を仕事に変換出来る割合には限界があるのではないかという問題を解決するために考え出された,二つの熱源の間に働く理想化された可逆な熱機関がカルノー機関です.一般に熱機関の効率はカルノー機関の効率を超えることはできません.カルノー機関の動作サイクルをカルノーサイクルといいます.

ジュールの実験によると,仕事は100%熱に変換することができます.しかしながら熱を100%仕事に変換することは経験上できません. 熱機関の効率が\(\eta=1\)になるようにするには，低温側の熱源に放出する熱量\(Q^{−}\)をそのまま高温側の熱源に戻すことになりますが,このとき熱機関では,「高温側の熱源のみから熱量\(Q=Q^{+}−Q^{−}\)を吸収し,それをすべて仕事\(W\)に変換するだけの過程」が実現していることになります.しかし,“仕事が熱に変わる現象は不可逆である” という経験事実は,『一様な温度をもつ１つの熱源から熱を吸収し,それをすべて仕事に変換するだけで,他に何の変化も残さないような過程は不可能である』ことを意味します.従って,この過程は実現できないことになります. “仕事が熱に変わる現象は不可逆である” という経験事実を述べたのがトムソンの原理です. また，低温側の熱源に放出した熱量\(Q^{−}\)をそっくり高温側の熱源にもどすときには,「低温側の熱源から高温側の熱源に熱\(Q^{−}\)を移すだけの過程」が実現していることになります.しかし,“熱が高温から低温に移る現象は不可逆である” という経験事実は,『ある温度の熱源からより高温の熱源に熱を移すのみで,他に何の変化も残さないような過程は不可能である』ことを意味します.そのため,やはりこの過程も実現できないことになります. “熱が高温から低温に移る現象は不可逆である”という経験事実を述べたのがクラウジウスの原理です. このように.熱機関の効率を\(\eta=1\)にできないという事実は,熱力学的な過程が一般的には不可逆であるという事実と密接な関係にあります.

クラウジウスの不等式

全系が外部系と,外部系とは壁で断熱された着目する系よりなるとします.着目する系と外部系はそれぞれ異なる温度(着目する系\(T\),外部\(T^{\rm e}\)で平衡状態にあったとします.ある時刻に系と外部系の壁を極めて熱の流れがよくない壁に代えると,着目する系と外部との間には熱の移動が起こり始めます. 熱の流れが遅いために着目する系も外部系も,各々が平衡状態にあると見なせます.つまり着目する系も外部系も熱の移動は準静的な過程であるとします.
外部系から着目する系へ流れ込む熱を\(d^{\prime}Q\)とするとそれぞれのエントロピーの変化は
着目する系に対して
\[
\Delta S =\int \frac{d^{\prime}Q}{T}
\]
外部系に対して
\[
\Delta S^{\rm e}=\int -\frac{d^{\prime}Q}{T^{\rm e}}　　　　　　　　
\]
となり、全系のエントロピー変化は
\[
\Delta S_{\rm total}=\Delta S + \Delta S^{\rm e} =\int \left(\frac{1}{T} −\frac{1}{T_{\rm e}}\right)d^{\prime}Q
\]
\( T < T^{\rm e}\)ならば\(d^{\prime}Q>0\), \(T>T^{\rm e}\) ならば\(d^\prime Q < 0\)となって,いずれにせよ \[ \int\frac{d^{\prime}Q}{T^{\rm e}} \leq \Delta S \] が成立します. 準静的過程でひとサイクルして最初の状態に戻った時\(\Delta S = 0\)となりますから \[ 　　　　　　　　　　　　　　　　　　\oint \frac{d^{\prime}Q}{T^{\rm e}}\leq 0 \] が成立します. この不等式はサイクル過程における熱の出入りに制限があることを示しています.エネルギー保存則により,サイクル過程では熱の出入りの総量は着目系が外部系にした仕事の総量等しいはずですから,仕事の総量にも制限があることを示しています.このクラウジウスの不等式は第二法則の弱い表現になっています. 準静過程でのエントロピーの定義から, \[ \Delta S=\int \frac{d^{\prime}Q}{T} \mbox{(準静的過程, 積分は始状態Aから終状態Bまで)} \] 熱平衡状態\(A\)から他の平衡状態\(B\)に至るエントロピー変化は経路によらず始点\(A\)と終点\(B\)だけで決まりますから, \[ \int \frac{d^{\prime}Q}{T}=S(B)-S(A) \] と書けます. \(A\)から\(B\)に至る一般的な過程に\(B\)から\(A\)への準静的過程を付け加えてサイクルを作りクラウジウスの不等式を適用すると, \[ \oint_{(A\rightarrow B)}\frac{d’Q}{T^{\rm e}} + S(A)-S(B)\leq 0 \] この関係で始めと終わりの状態は熱平衡状態であり,断熱過程で他の平衡状態に移動した場合は\(\Delta S=0\)となりますから, \(S(A)-S(B)\leq 0\)となって,エントロピーは減少することはないことを示しています. 　　

5. 熱力学の第三法則

熱力学の第三法則はネルンストの熱定理またはネルンスト＝プランクの定理ともいます. 絶対零度でのエントロピーに関する法則で,1906年 W.H.ネルンストは絶対零度に近づけばエントロピー\(S\)の変化\(\Delta S\)はゼロに近づくことを主張し,さらに M.プランクはエントロピー自身がゼロに近づくことを主張しました. 熱力学の枠内ではネルンストの定理はエントロピーの原点\((S = 0)\)を定めるものとされます.
これは次のように説明出来ます.

圧力を一定に保ったまま系を準静的に熱したとします.このようにして\(d^{\prime}Q\)だけの熱を加えたときの系の温度変化を\(dT\)とすると,両者の比
\[
C_p \equiv \lim_{d^{\prime}Q \rightarrow 0}\left(\frac{d^{\prime}Q}{dT}\right)_p
\]
を,定圧熱容量と呼びます.　準静的過程ですから\(d^{\prime}Q=TdS\)となって\(C_p\)は以下の通りに書くことが出来ます.
\[
C_p=-T\left(\frac{\partial S}{\partial T}\right)_p = −B\left(\frac{\partial S}{\partial B}\right)_p
\]
\(C_p\)は負にはなれません.もしもその物体があるとすれば,その物体から熱を取ることにより温度が上ることになり,これは,熱力学の第二法則 に反します. 従って\((\partial B/\partial T)_p<0\)で, エントロピーは\(B\)の単調減少関数(\(T\)の単調増加関数)になります. エントロピーも\(B\)も常に負にはなれないので, ｢\(B\)が無限に大きくなるにつれ,エントロピーは常に\(0\)に近づく｣ということが言えます.すなわちこれが熱力学の第三法則です. ネルンストの定理を別の表現にすると,有限回の操作では決して,絶対零度には到達することができないという定理になります.すなわち,物体を冷却するにはその温度以下の別の物体と接触させる方法が一般的であるがこの場合は絶対零度以下の物体と接触させなければならない.しかし絶対零度より低い温度を持つ物体はないのでこれは不可能である. 断熱膨張によって内部エネルギーを放出させて温度を下げる方法もあるが,限りなく絶対零度に近づけることはできても無限に膨張させることができなければ厳密な意味での絶対零度には到達できない. \(T=0\)に近づくと\(\Delta S\)はも0に近づくためと\(d^{\prime}Q\)も\(0\)になるため有限回の操作では\(T=0\)に到達できないことを示しています なお,熱力学第三法則は第一法則と第二法則から導くことができるので物理学の基本法則ではない,とする考えもあります. しかし熱力学は第一法則と第二法則だけでは成立せず, エントロピーの原点(\(S=0\))を定める第三法則を加えることによって初めて完成することになります. ネルンスト自身はこの定理について,「熱力学第一法則は3人(マイヤー, ジュール, ヘルムホルツ), 第二法則は2人(カルノー, クラウジウス), 第三法則は1人(ネルンスト)によって発見された. 第四法則を発見する人は0人になってしまうから,熱力学はこれで完成された」と語っているそうです.

終わりに

熱力学の基本法則をごく簡単に説明してきました. 熱力学の第一および第二法則でによるとエネルギーとエントロピーは密接な関係があり,重要な役割を果たすことを見てきました.これらは地球環境においても重要な役割を担います.

熱は人間の活動の根源ともいえますが, 現在エネルギー資源の浪費とその結果としての環境汚染や地球温暖化が危機的な状況となってきております. 私たちの生存のためには一定の温度を維持する必要がありますが, その温度を維持するためには, 地上の不可逆反応で増大したエントロピーを減少させることが必要とされています.

地球は高温で熱を得て低温で熱を放出するサイクルでエントロピーを減少させています. 太陽の輻射熱と海と大気の循環で放出される熱を\(Q\)として,\(\Delta S\)を輻射のエントロピー, \(\Delta S^{\rm e}\)を循環のエントロピー,\(T^{\rm e}\)を地球の温度とすると
\[
\Delta S_{\rm total}=\Delta S +\Delta S^{\rm e}=\left(\frac{1}{T}-\frac{1}{T^{\rm e}}\right)Q
\]
で, 確かに負になります. 太陽の輻射熱が変わらないと仮定して,環境の温度が高くなるとエントロピー減少の度合いが.低くなります. つまり今後とも生存を保証するためには地球温暖化を止めなければならないわけです.

このように生活環境としての地球を理解する上でも熱(力)学の知識が必要で, 熱(力)学を学ぶことには大きな意義があると考えます.
<文/本田耕一郎>